Cho tam giác ABC có AB < AC. Gọi E, F lần lượt là trung điểm AB, AC.
a) Chứng minh: EF là đường trung bình của tam giác ABC.
b) Gọi J là trung điểm BC. Đoạn thẳng AJ cắt đoạn thẳng EF tại S. Chứng minh S là trung điểm EF.
c) Kẻ đường cao AH của tam giác ABC. Đoạn thẳng HF và EJ cắt nhau tại I. Chứng minh SI // AH.





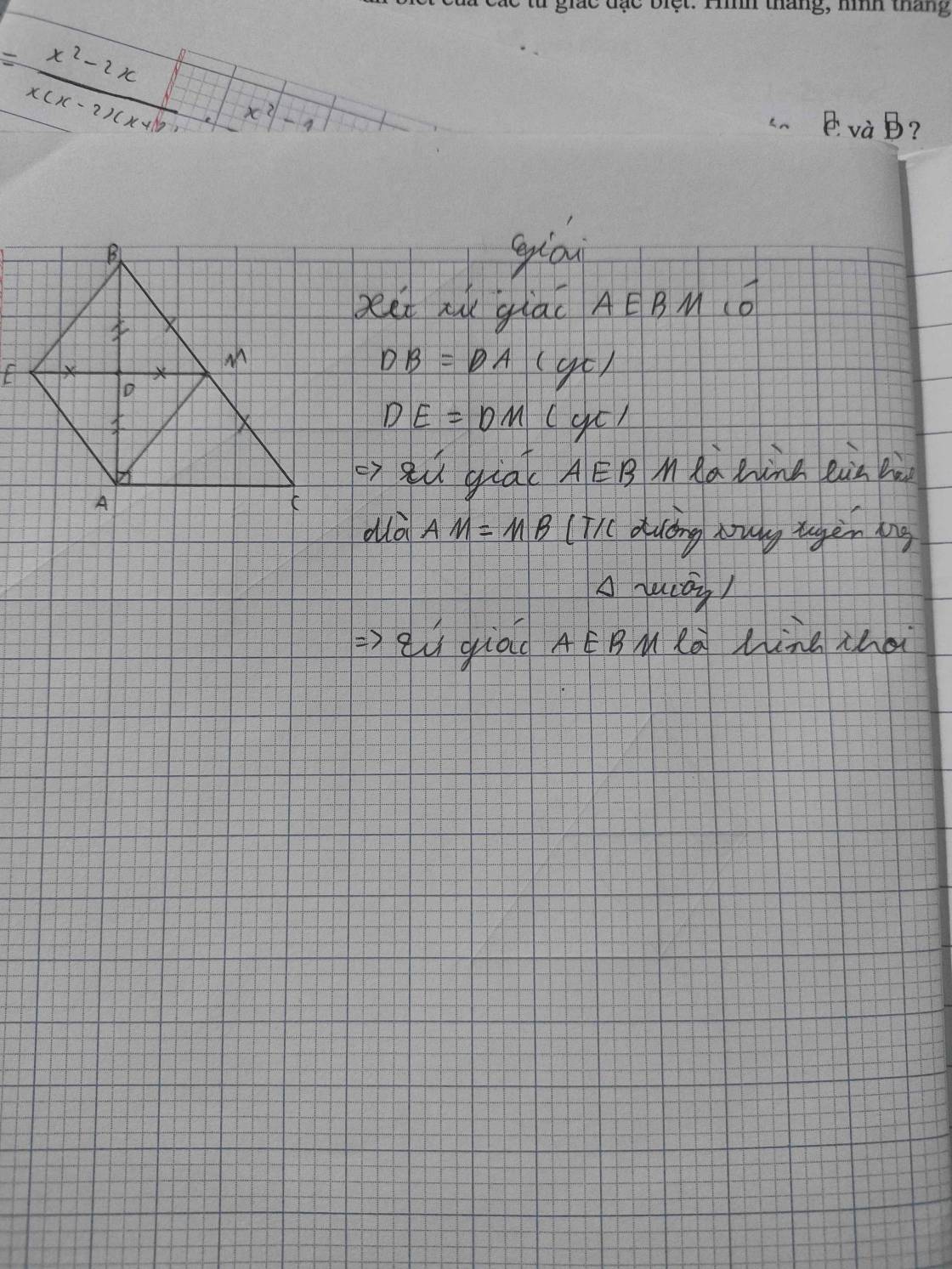
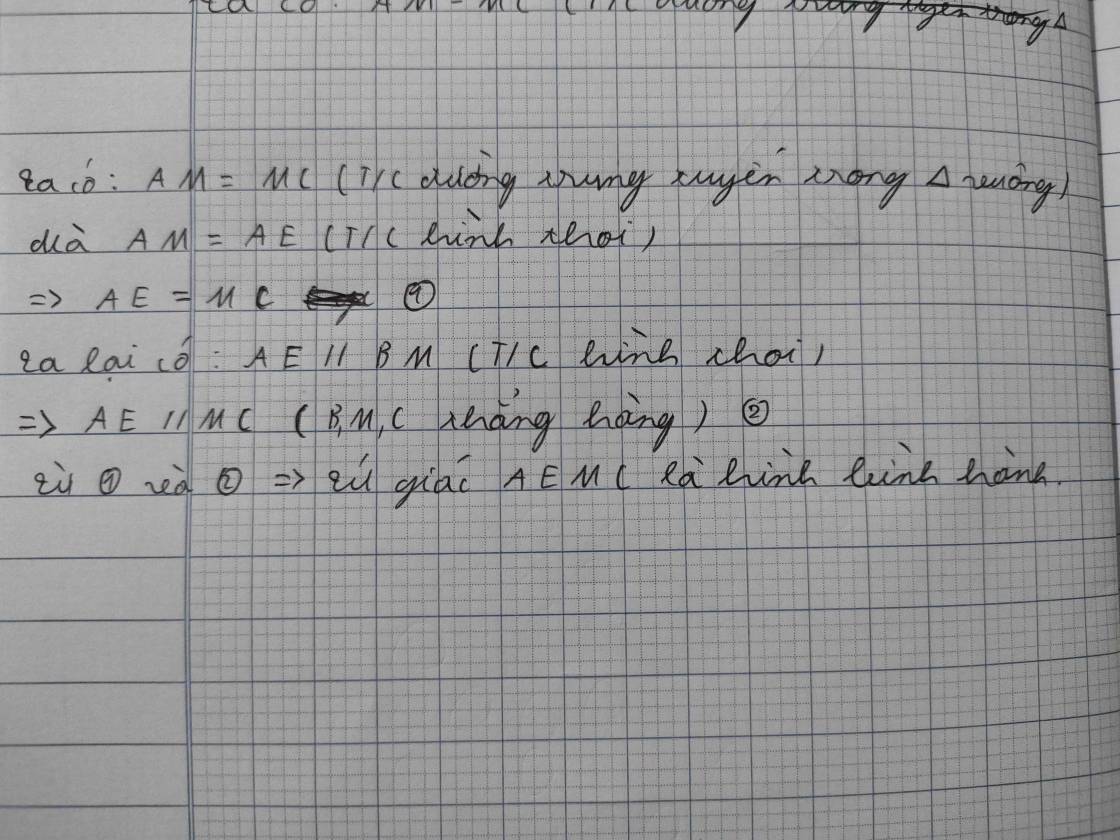
 Giúp mk c15 c16 vs ạ
Giúp mk c15 c16 vs ạ