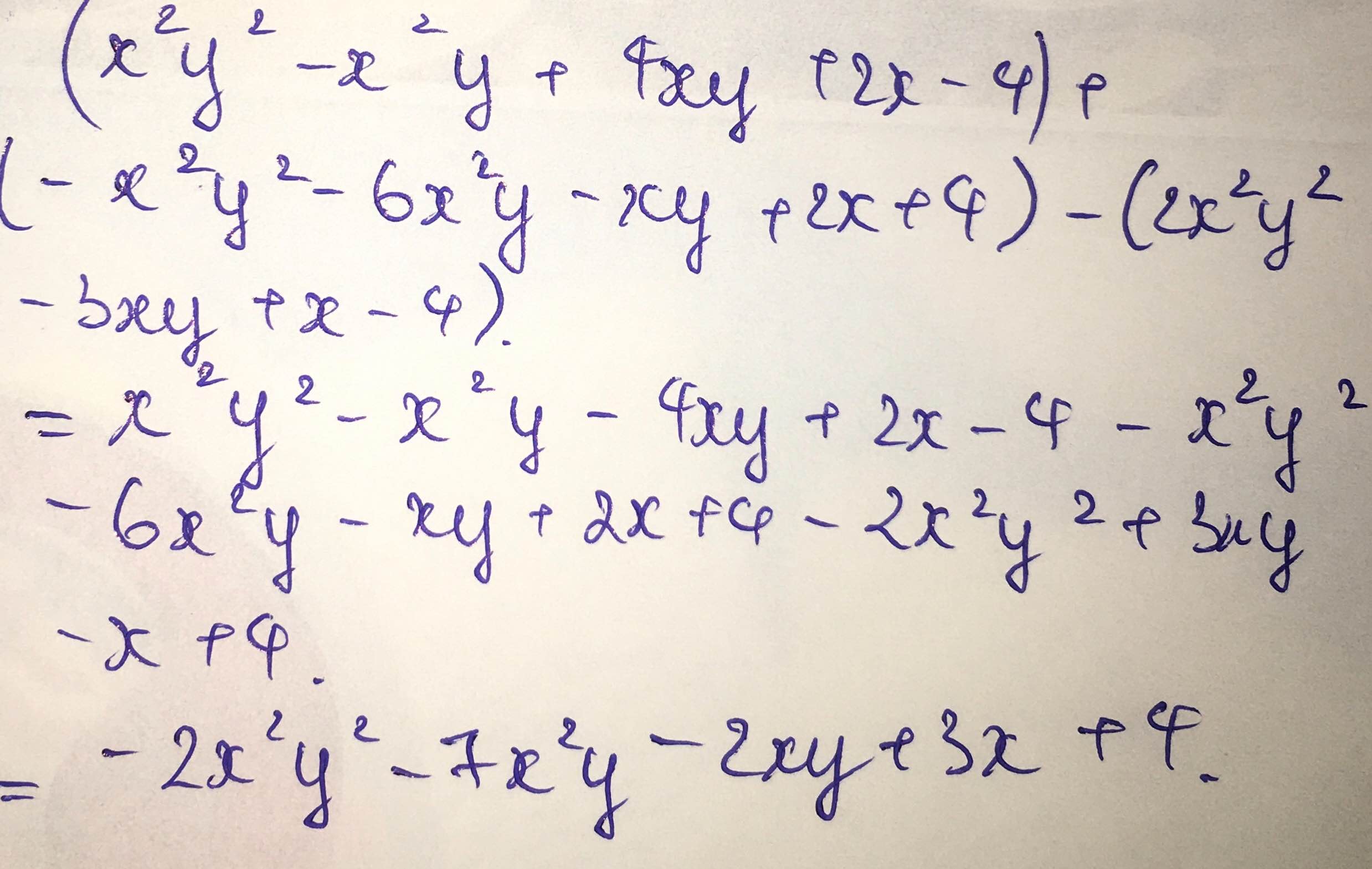x^2+2y^2-3xy+x-2y
PK
Những câu hỏi liên quan
Tìm x
a) x(x^3+3x-4x)-(4x+3x^2)=20
b) (2\3xy-x^2+3xy^3)(2x^2-3xy^2+x^2y)
c) (2xy+3xy^2-x^2y)(xy+x^2y+y^2)
hihihihihihhihihhihihihhihihihhihihhihi
Đúng 0
Bình luận (0)
(x^2y^2 - x^2y + 4xy + 2x - 4) + (-x^2y^2 - 6x^2y - xy + 2x+4) - (2x^2y^2 - 3xy +x - 4)
=
P=-3xy(xy-2y^2)-x^2(x^2-y^2)+2y^2(x^2-3xy tại x=-2 y=2011 tại x=-2;y=2011
\(P=-3xy\left(xy-2y^2\right)-x^2\left(x^2-y^2\right)+2y^2\left(x^2-3xy\right)\)
\(P=-3x^2y^2+6xy^3-x^4+x^2y^2+2x^2y^2-6xy^3\)
\(P=-x^4\)
Thay x = -2 vào P, ta có:
\(P=-\left(-2\right)^4=-16\)
Đúng 1
Bình luận (0)
Ta có: \(P=-3xy\left(xy-2y^2\right)-x^2\left(x^2-y^2\right)+2y^2\left(x^2-3xy\right)\)
\(=-3x^2y^2+6xy^3-x^4+x^2y^2+2x^2y^2-6xy^3\)
\(=-x^4\)
\(=-16\)
Đúng 1
Bình luận (0)
Bai 1 TINH
a) x ^2 . x -2x^3
b) 6 x^2y . 3xy - 2y^2.x +y
C) 4x^2 +5x -1 .2x^3 -3x
d)-8x^3y + 2y^4 . 3xy^3 - 2x^4 +7y^4
GIUP MINH NHÀ
a.4x^2y-3xy^2+xy+xy-x^2y+5xy^2
b.x^2+2y^2+3xy+x^2-3y^2+4xy
c.2x^y-3xy+4xy^2-5x^2y+2xy^2
d.(2x^3+3x^2-4x+1)-(3x+4x^3-5)
a (2y^3-5y^2+6y-15):(2y-5)
b 7/y-y/y+6+36/y^2+6y
c 5x+2/3xy^2:10x+4/x^2y
d 1/5x^2y(15xy^2-5y+3xy)
e (x-y)(x-y)-x(x-1)
Mọi người giúp e với ạ
Xem chi tiết
Bạn viết đề cẩn thận bằng công thức toán thì sẽ tăng khả năng nhận được sự giúp đỡ hơn. Viết như thế này nhìn rối mắt cực.
Đúng 0
Bình luận (0)
a) (x^2-2x+3).(1/2x-5) b) (x^2y^2 -1/3xy+2y).(x-2y)
\(a,\left(x^2-2x+3\right)\left(\dfrac{1}{2}x-5\right)\\ =x^2.\dfrac{1}{2}x-5x^2-2x.\dfrac{1}{2}x+2x.5+3.\dfrac{1}{2}x-15\\ =\dfrac{1}{2}x^3-5x^2-x^2+10x+\dfrac{3}{2}x-15\\ =\dfrac{1}{2}x^3-6x^2+\dfrac{23}{2}x-15\)
\(b,\left(x^2y^2-\dfrac{1}{3}xy+2y\right)\left(x-2y\right)\\ =x^3y-2x^2y^3-\dfrac{1}{3}x^2y+\dfrac{2}{3}xy^2+2xy-4y^2\)
Đúng 1
Bình luận (2)
a) \(\left(x^2-2x+3\right)\left(\dfrac{1}{2}x-5\right)\)
\(=\dfrac{1}{2}x^3-5x^2-x+10x+\dfrac{3}{2}x-15\)
\(=\dfrac{1}{2}x^3-5x^2+\dfrac{48}{5}x-15\)
b) \(\left(x^2y^2-\dfrac{1}{3}xy+2y\right)\left(x-2y\right)\)
\(=x^3y^2-2x^2y^3-\dfrac{1}{3}x^2y+\dfrac{2}{3}xy^2+2xy-4y^2\)
Đúng 0
Bình luận (2)
giúp với ạ
Rút gọn
a, ( x + y ) . ( x + y ) mũ 2– 3xy . ( x + y )
b, ( x – y ) . ( x – y ) mũ 2 – 3xy . ( x – y)
c, ( x – 2y) mũ 2 + 4y mũ 2
d, ( 3x – 2y ) mũ 2 + 12xy
e, ( x – 3y ) . ( x + 3y ) – ( x – 2y ) mũ 2
Đọc tiếp
giúp với ạ
Rút gọn
a, ( x + y ) . ( x + y ) mũ 2– 3xy . ( x + y )
b, ( x – y ) . ( x – y ) mũ 2 – 3xy . ( x – y)
c, ( x – 2y) mũ 2 + 4y mũ 2![]()
d, ( 3x – 2y ) mũ 2 + 12xy
e, ( x – 3y ) . ( x + 3y ) – ( x – 2y ) mũ 2![]()
a, (\(x\) + y).(\(x\) + y)2 - 3\(xy\).(\(x\) + y)
= (\(x+y\))3 - 3\(x^2\)y - 3\(xy^2\)
= \(x^3\) + 3\(x^2\).y + 3\(xy^2\) + y3 - 3\(x^2\).y - 3\(xy^2\)
= \(x^3\) + y3
Đúng 0
Bình luận (0)
b, (\(x-y\)).(\(x-y\))2 - 3\(xy\).(\(x-y\))
= (\(x\) - y)3 - 3\(x^2\).y + 3\(xy^2\)
= \(x^3\) - 3\(x^2\)y + 3\(xy^2\) - y3 - 3\(x^2\)y + 3\(xy^2\)
= \(x^3\) - 6\(x^2\)y + 6\(xy^2\) - y3
Đúng 0
Bình luận (0)
c, (\(x\) - 2y)2 + 4y2
= \(x^2\) - 4\(xy\) + 4y2 + 4y2
= \(x^2\) - 4\(xy\) + 8y2
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Rút gọn phân thức x^2+3xy+2y^2/x^3+2x^2y-xy^2-2y^3
\(\dfrac{x^2+3xy+2y^2}{x^3+2x^2y-xy^2-2y^3}\)
\(=\dfrac{\left(x+y\right)\left(x+2y\right)}{x\left(x^2-y^2\right)+2y\left(x^2-y^2\right)}\)
\(=\dfrac{x+y}{x^2-y^2}\)
\(=\dfrac{1}{x-y}\)
Đúng 0
Bình luận (0)