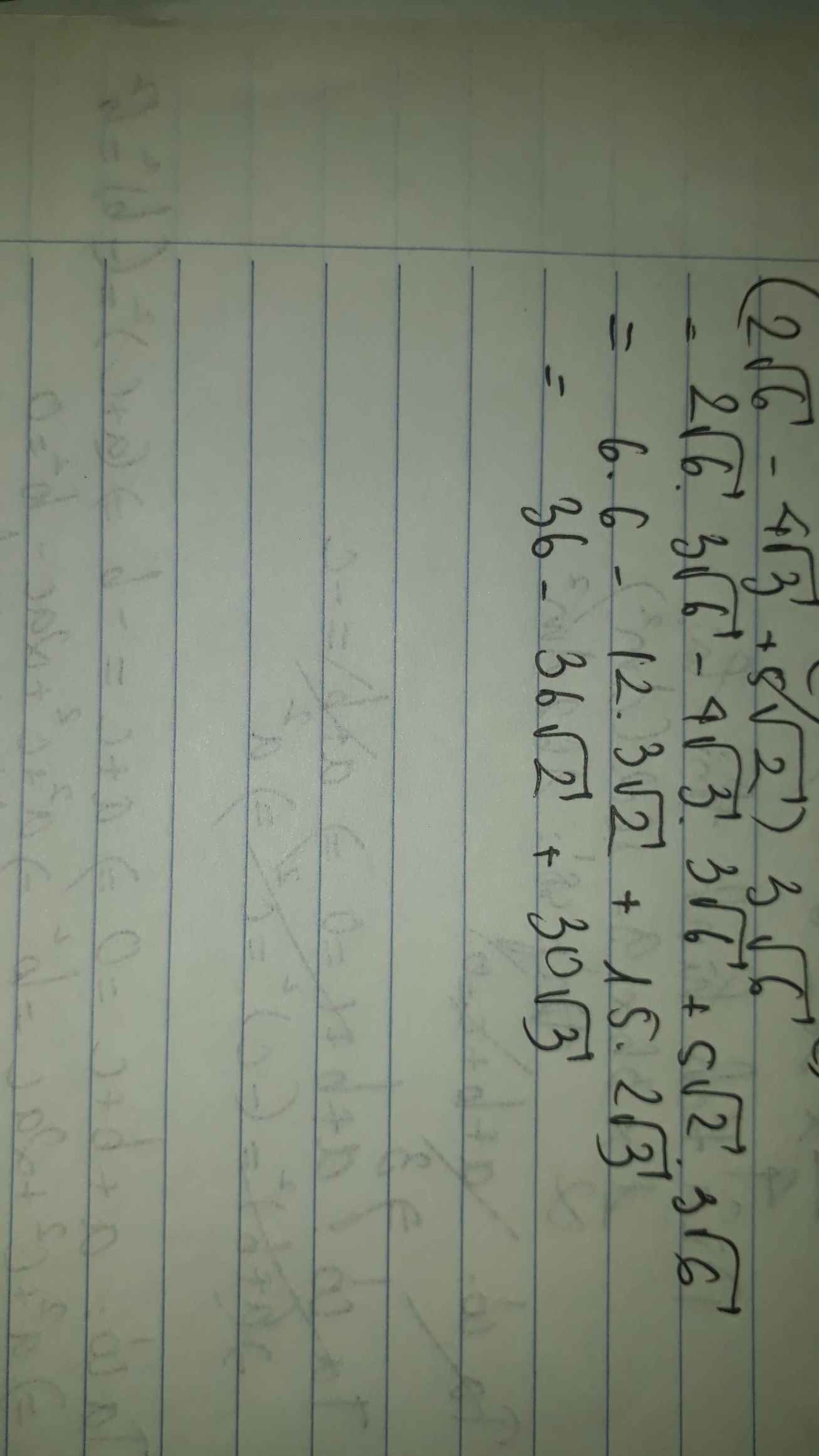\(\left(2\sqrt{6}-4\sqrt{3}+5\sqrt{2}\right)\cdot3\sqrt{6}\)

\(=2\sqrt{6}\cdot3\sqrt{6}-4\sqrt{3}\cdot3\sqrt{6}+5\sqrt{2}\cdot3\sqrt{6}\)

\(=36-36\sqrt{2}+30\sqrt{3}\)

\(\sqrt{x^2-2x+4}+\sqrt{x^2+5}=9-2x\left(đk:x\le\dfrac{9}{2}\right)\)

\(\Leftrightarrow x^2-2x+4+x^2+5+2\sqrt{\left(x^2-2x+4\right)\left(x^2+5\right)}=81-36x+4x^2\)

\(\Leftrightarrow2\sqrt{\left(x^2-2x+4\right)\left(x^2+5\right)}=2x^2-34x+72\)

\(\Leftrightarrow4\left(x^2-2x+4\right)\left(x^2+5\right)=4x^4+1156x^2+5184-136x^3+288x^2-4896x\)

\(\Leftrightarrow4x^4-8x^3+36x^2-40x+80=4x^4-136x^3+1444x^2-4896x+5184\)

\(\Leftrightarrow128x^3-1408x^2+4856x-5104=0\)

\(\Leftrightarrow128x^2\left(x-2\right)-1152x\left(x-2\right)+2552\left(x-2\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(128x^2-1152x+2552\right)=0\)

\(\Leftrightarrow x=2\left(tm\right)\)(do \(128x^2-1152x+2552>0\))

Bạn ghi thiếu đề hoặc đề sai không vậy??

Biểu thức không bằng một giá trị nào đó thì sao tìm x được :>

a) Để \(\dfrac{\sqrt{x}}{\sqrt{x}-3}\) có nghĩa khì \(x\ge0;x\ne9\)

b) Để \(\dfrac{\sqrt{x}}{\sqrt{x}+6}\) có nghĩa khi \(x\ge0\)

đoạn cuối thiếu dấu"+"

\(A=\dfrac{\sqrt{4}-\sqrt{5}}{4-5}+\dfrac{\sqrt{5}-\sqrt{6}}{5-6}+....+\dfrac{\sqrt{34}-\sqrt{35}}{34-35}+\dfrac{\sqrt{35}-\sqrt{36}}{335-36}\)

\(A=\dfrac{\sqrt{4}-\sqrt{5}+\sqrt{5}-\sqrt{6}+....+\sqrt{35}-\sqrt{36}}{-1}=\dfrac{\sqrt{4}-\sqrt{36}}{-1}\)

\(A=\sqrt{36}-\sqrt{4}=6-2=4\)

\(\dfrac{1}{\sqrt{4}+\sqrt{5}}+\dfrac{1}{\sqrt{5}+\sqrt{6}}+\dfrac{1}{\sqrt{6}+\sqrt{7}}+...+\dfrac{1}{\sqrt{34}+\sqrt{35}}+\dfrac{1}{\sqrt{35}+\sqrt{36}}\)

\(=-\sqrt{4}+\sqrt{5}-\sqrt{5}+\sqrt{6}-...-\sqrt{35}+\sqrt{36}\)

\(=6-2=4\)

    1. Phương pháp 1: ( Hình 1)

        Nếu  thì ba điểm A; B; C thẳng hàng.

    2. Phương pháp 2: ( Hình 2)

        Nếu AB // a và AC // a thì ba điểm A; B; C thẳng hàng.

       (Cơ sở của phương pháp này là: tiên đề Ơ – Clit- tiết 8- hình 7)

    3. Phương pháp 3: ( Hình 3)

        Nếu AB  a ; AC  A thì ba điểm A; B; C thẳng hàng.

        ( Cơ sở của phương pháp này là: Có một và chỉ một đường thẳng

        a^’ đi qua điểm O và vuông góc với đường thẳng a cho trước

        - tiết 3 hình học 7)

        Hoặc A; B; C cùng thuộc một đường trung trực của một

        đoạn thẳng .(tiết 3- hình 7)

    4. Phương pháp 4: ( Hình 4)

        Nếu tia OA và tia OB là hai tia phân giác của góc xOy

        thì ba điểm O; A; B thẳng hàng.

        Cơ sở của phương pháp này là:                                                        

        Mỗi góc có một và chỉ một tia phân giác .

     * Hoặc : Hai tia OA và OB cùng nằm trên nửa mặt phẳng bờ chứa tia Ox ,

                   thì ba điểm O, A, B thẳng hàng.

    5. Nếu K là trung điểm BD, K^’ là giao điểm của BD và AC. Nếu K^’

       Là trung điểm BD  thì K^’  K thì A, K, C thẳng hàng.

      (Cơ sở của phương pháp này là: Mỗi đoạn thẳng chỉ có một trung điểm)

C. Các ví dụ minh họa cho tùng phương pháp:

                                                                Phương pháp 1

    Ví dụ 1. Cho tam giác ABC vuông ở A, M là trung điểm AC. Kẻ tia Cx vuông góc CA

                     (tia Cx và điểm B ở hai nửa mặt phẳng đối nhau bờ AC). Trên tia Cx lấy điểm

                     D sao cho CD = AB.

                     Chứng minh ba điểm B, M, D thẳng hàng.

     Gợi ý: Muốn B, M, D thẳng hàng cần chứng minh

               Do nên cần chứng minh

BÀI GIẢI:

               AMB và CMD có:                                                       

                   AB = DC (gt).

                    MA = MC (M là trung điểm AC)                                              

               Do đó: AMB = CMD (c.g.c). Suy ra:

               Mà   (kề bù) nên .

               Vậy ba điểm B; M; D thẳng hàng.

    Ví dụ 2. Cho tam giác ABC. Trên tia đối của AB lấy điểm D mà  AD = AB, trên tia đối

                     tia AC lấy điểm E mà AE = AC. Gọi M; N lần lượt là các điểm trên BC và ED

                      sao cho CM = EN.

                    Chứng minh ba điểm M; A; N thẳng hàng.

Gợi ý: Chứng minh  từ đó suy ra ba điểm M; A; N thẳng hàng.

BÀI GIẢI (Sơ lược)

          ABC = ADE (c.g.c)

          ACM = AEN (c.g.c)

          Mà  (vì ba điểm E; A; C thẳng hàng) nên

Vậy ba điểm M; A; N thẳng hàng (đpcm)

BÀI TẬP THỰC HÀNH CHO PHƯƠNG PHÁP 1

Bài 1: Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho AD = AC, trên tia đối

          của tia AC lấy điểm E sao cho AE = AB. Gọi M, N lần lượt là trung điểm của BE và

          CD.

          Chứng minh ba điểm M, A, N thẳng hàng.

Bài 2: Cho tam giác ABC vuông ở A có . Vẽ tia Cx  BC (tia Cx và điểm A ở

          phía ở cùng phía bờ BC), trên tia Cx lấy điểm E sao cho CE = CA. Trên tia đối của tia

          BC lấy điểm F sao cho BF = BA.

          Chứng minh ba điểm E, A, F thẳng hàng.

Bài 3: Cho tam giác ABC cân tại A, điểm D thuộc cạnh AB. Trên tia đối của tia CA lấy điểm

          E sao cho CE = BD. Kẻ DH và EK vuông góc với BC (H và K thuộc đường thẳng BC)

          Gọi M là trung điểm HK.

          Chứng minh ba điểm D, M, E thẳng hàng.

Bài 4: Gọi O là trung điểm của đoạn thẳng AB. Trên hai nửa mặt phẳng đối nhau bờ AB, kẻ

          Hai tia Ax và By sao cho .Trên Ax lấy hai điểm C và E(E nằm giữa A và C),

          trên By lấy hai điểm D và F ( F nằm giữa B và D) sao cho AC = BD, AE = BF.

          Chứng minh ba điểm C, O, D thẳng hàng , ba điểm E, O, F thẳng hàng.

Bài 5.Cho tam giác ABC . Qua A vẽ đường thẳng xy // BC. Từ điểm M trên cạnh BC, vẽ các

          đường thẳng song song AB và AC, các đường thẳng này cắt xy theo thứ tự tại D và E.

          Chứng minh các đường thẳng AM, BD, CE cùng đi qua một điểm.

                                                              PHƯƠNG PHÁP 2

    Ví dụ 1: Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của các cạnh AC, AB. Trên

                  Các đường thẳng BM và CN lần lượt lấy các điểm D và E sao cho M là trung  

                 điểm BD và N là trung điểm EC.

                  Chứng minh ba điểm E, A, D thẳng hàng.

Hướng dẫn: Xử dụng phương pháp 2                                            

                  Ta chứng minh AD // BC và AE // BC.

BÀI GIẢI.

                 BMC và DMA có:

                   MC = MA (do M là trung điểm AC)

                    (hai góc đối đỉnh)

                   MB = MD (do M là trung điểm BD)

                  Vậy: BMC = DMA (c.g.c)

                   Suy ra: , hai góc này ở vị trí so le trong nên BC // AD (1)

                   Chứng minh tương tự : BC // AE (2)

                   Điểm A ở ngoài BC có một và chỉ một đường thẳng song song BC nên từ (1)

                   và (2) và theo Tiên đề Ơ-Clit suy ra ba điểm E, A, D thẳng hàng. 

   Ví dụ 2: Cho hai đoạn thẳng  AC và BD cắt nhau tai trung điểm O của mỗi đoạn. Trên tia

                 AB lấy lấy điểm M sao cho B là trung điểm AM, trên tia AD lấy điểm N sao cho

                 D là trung điểm AN. 

1/ \(x^3+2=3\sqrt[3]{3x-2}\)

Đặt \(\sqrt[3]{3x-2}=a\) thì ta có hệ

\(\hept{\begin{cases}x^3+2-3a=0\\a^3+2-3x=0\end{cases}}\)

Lấy trên - dưới ta được

\(x^3-a^3+3x-3a=0\)

\(\Leftrightarrow\left(x-a\right)\left(x^2+ax+a^2+3\right)=0\)

\(\Leftrightarrow x=a\)

\(\Leftrightarrow x=\sqrt[3]{3x-2}\)

\(\Leftrightarrow x^3-3x+2=0\)

\(\Leftrightarrow\orbr{\begin{cases}x=1\\x=-2\end{cases}}\)

2/ \(x+\sqrt{5-x^2}+x\sqrt{5-x^2}=5\)

Đặt \(\sqrt{5-x^2}=a\ge0\) thì ta có hệ

\(\hept{\begin{cases}x+a+ax=5\\a^2+x^2=5\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}x+a+ax=5\\\left(a+x\right)^2-2ax=5\end{cases}}\)

Tới đây thì đơn giản rồi. Đặt \(\hept{\begin{cases}a+x=S\\ax=P\end{cases}}\) giải tiếp sẽ ra

a) Ta có: \(\frac{6}{\sqrt{2}-\sqrt{3}+3}\)

\(=\frac{6\left(\sqrt{2}-\sqrt{3}-3\right)}{\left(\sqrt{2}-\sqrt{3}+3\right)\left(\sqrt{2}-\sqrt{3}-3\right)}\)

\(=\frac{6\left(\sqrt{2}-\sqrt{3}-3\right)}{5-2\sqrt{6}-9}\)

\(=\frac{6\left(\sqrt{2}-\sqrt{3}-3\right)}{-4-2\sqrt{6}}\)

\(=\frac{6\left(\sqrt{2}-\sqrt{3}-3\right)}{-2\sqrt{2}\left(\sqrt{2}-\sqrt{3}\right)}\)

\(=\frac{3\left(\sqrt{2}-\sqrt{3}-3\right)\left(\sqrt{2}+\sqrt{3}\right)}{-\sqrt{2}\left(\sqrt{2}-\sqrt{3}\right)\left(\sqrt{2}-\sqrt{3}\right)}\)

\(=\frac{3\sqrt{2}\left(\sqrt{2}+\sqrt{3}\right)\left(\sqrt{2}-\sqrt{3}-3\right)}{2}\)

b) Ta có: \(\left(\frac{4}{\sqrt{5}+1}-\frac{4}{\sqrt{5}-1}\right):\sqrt{3+2\sqrt{2}}\)

\(=\left(\frac{4\left(\sqrt{5}-1\right)}{\left(\sqrt{5}+1\right)\left(\sqrt{5}-1\right)}-\frac{4\left(\sqrt{5}+1\right)}{\left(\sqrt{5}+1\right)\left(\sqrt{5}-1\right)}\right):\sqrt{2+2\cdot\sqrt{2}\cdot1+1}\)

\(=\left(\frac{4\left(\sqrt{5}-1\right)}{4}-\frac{4\left(\sqrt{5}+1\right)}{4}\right):\sqrt{\left(\sqrt{2}+1\right)^2}\)

\(=\left(\sqrt{5}-1-\sqrt{5}-1\right):\left|\sqrt{2}+1\right|\)

\(=-\frac{2}{\sqrt{2}+1}\)(Vì \(\sqrt{2}+1>0\))

\(=-\frac{2\left(\sqrt{2}-1\right)}{\left(\sqrt{2}+1\right)\left(\sqrt{2}-1\right)}\)

\(=-2\left(\sqrt{2}-1\right)\)

\(=-2\sqrt{2}+2\)

6 + 2 căn 2 + 2 căn 3 + 2 căn 6 = (1 + căn 2 + căn 3)² 

5 + 2 căn 6 = (căn 2 + căn 3)²

tự giải tieeps nha bn ^^