Rút gọn biểu thức sau
A=sinx -sin2x / cosx +cos2x
Rút gọn biểu thức A = sinx + sin2x + sin3x/cosx + cos2x + cos3x
`A=[sin x + sin 2x + sin 3x]/[cos x + cos 2x + cos 3x]`
`A=[2sin2x.cosx+sin2x]/[2cos2x.cosx+cos2x]`
`A=[sin2x(2cosx+1)]/[cos2x(2cosx+1)]`
`A=tan 2x`
\(A=\dfrac{sinx-sin2x+sin3x}{cosx-cos2x+cos3x}\)
\(ĐK\left\{{}\begin{matrix}cos2x\ne0\\cosx\ne\dfrac{1}{2}\end{matrix}\right.\) \(\Leftrightarrow\) \(A=\dfrac{sinx+sin3x-sin2x}{cosx+cos3x-cos2x}\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}=\dfrac{2sin2x.cosx-sin2x}{2cos2x.cosx-cos2x}\\=\dfrac{sin2x\left(2cosx-1\right)}{cos2x\left(2cosx-1\right)}\end{matrix}\right.\) \(\Rightarrow\) \(A=tan2x\)
Rút gọn biểu thức sau ta được biểu thức nào sau đây?
A = c o s 2 x + sin 2 x + sin 2 x 2 sin x + c o s x
A. cosx
B. sinx
C. tanx
D. cotx
Đáp án: A
Ta có:
A = c o s 2 x + sin 2 x + sin 2 x 2 sin x + c o s x
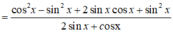
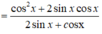
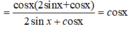
Rút gọn
A = \(\dfrac{sinx+sin2x+sin3x}{cosx+cos2x+cos3x}\)
`A=[sin x+sin 2x+sin 3x]/[cos x+cos 2x+cos 3x]`
`A=[(sin x+sin 3x)+sin 2x]/[(cos x+cos 3x)+cos 2x]`
`A=[2sin 2x.cos (-x)+sin 2x]/[2cos 2x.cos (-x)+cos 2x]`
`A=[sin 2x(2cos(-x)+1)]/[cos 2x(2cos(-x)+1)]`
`A=[sin 2x]/[cos 2x]=tan 2x`.
Rút gọn biểu thức
A = sin3x + cos2x - sinx/ cosx + sin2x - cos3x
( sin2x ≠0; 2sinx +1 ≠0)
\(A=\frac{sin3x-sinx+cos2x}{cosx-cos3x+sin2x}=\frac{2cos2x.sinx+cos2x}{2sin2x.sinx+sin2x}=\frac{cos2x\left(2sinx+1\right)}{sin2x\left(2sinx+1\right)}=\frac{cos2x}{sin2x}=cot2x\)
Rút gọn các biểu thức sau:
D = \(\frac{1+sin2x+cos2x}{1+sin2x-cos2x}\)E = \(\frac{sin2x+2sin3x+sin4x}{cos3x+2cos4x-cos5x}\)F = \(\frac{sinx+sin4x+sin7x}{cosx+cos4x+cos7x}\)G = \(\frac{cos2x-sin4x-cos6x}{cos2x+sin4x-cos6x}\)\(D=\frac{1+sin2x+cos2x}{1+sin2x-cos2x}=\frac{1+2sinxcosx+2cos^2x-1}{1+2sinxcosx-1+2sin^2x}\)
\(D=\frac{cosx\left(sinx+cosx\right)}{sinx\left(sinx+cosx\right)}=cotx\)
\(F=\frac{sinx+sin4x+sin7x}{cosx+cos4x+cos7x}\)
\(F=\frac{2sin4xcos3x+sin4x}{2cos4xcos3x+cos4x}\)
\(F=\frac{2sin4x\left(cos3x+1\right)}{2cos4x\left(cos3x+1\right)}=tan4x\)
\(G=\frac{cos2x-sin4x-cos6x}{cos2x+sin4x-cos6x}=\frac{-2sin4xsin2x-sin4x}{-2sin4xsin2x+sin4x}\)
\(G=\frac{-sin4x\left(2sin2x+1\right)}{-sin4x\left(2sin2x-1\right)}=\frac{2sin2x+1}{2sin2x-1}\)
Rút gọn biểu thức A = \(\frac{sinx+sin2x+sin3x}{cosx+cos2x+cos3x}\)
\(A=\frac{sinx+sin3x+sin2x}{cosx+cos3x+cos2x}=\frac{2sin2x.cosx+sin2x}{2cos2x.cosx+cos2x}=\frac{sin2x\left(2cosx+1\right)}{cos2x\left(2cosx+1\right)}=\frac{sin2x}{cos2x}=tan2x\)
\(sinx+4cosx=2+sin2x\)
\(\left(1-sin2x\right)\left(sinx+cosx\right)=cos2x\)
\(1+sinx+cosx+sin2x+cos2x=0\)
\(sinx+sin2x+sin3x=1+cosx+cos2x\)
\(sin^22x-cos^28x=sin\left(\dfrac{17\pi}{2}+10x\right)\)
Tính giá trị biểu thức:
cos2x - sin2x = sinx + cosx
Tiêu đề không phù hợp. Cái này là giải phương trình bạn nhá.
Lời giải:
PT $\Leftrightarrow 2\cos ^2x-1-2\cos x\sin x=\sin x+\cos x$
$\Leftrightarrow (2\cos ^2x-1-\cos x)-(2\cos x\sin x+\sin x)=0$
$\Leftrightarrow (\cos x-1)(2\cos x+1)-\sin x(2\cos x+1)=0$
$\Leftrightarrow (2\cos x+1)(\cos x-1-\sin x)=0$
Nếu $2\cos x+1=0\Rightarrow x=\pm \frac{2}{3}\pi +2k\pi$ với $k$ nguyên.
Nếu $\cos x-1-\sin x=0$
$\Leftrightarrow \cos x-\sin x=1$
$\Rightarrow \cos x=\sin x+1$
$\Rightarrow \cos ^2x=(\sin x+1)^2$
$\Leftrightarrow 1-\sin ^2x=(\sin x+1)^2$
$\Rightarrow \sin x=0$ hoặc $\sin x=-1$
Nếu $\sin x=0\Rightarrow \cos x=1$. Ta tìm được $x=2k\pi$ với $k$ nguyên
Nếu $\sin x=-1\Rightarrow \cos x=0$. Ta tìm được $x=2k\pi-\frac{\pi}{2}$ với $k$ nguyên.
Chứng minh các đẳng thức :
a) sin3x = 3sinx - 4sin3x
b) tan 2x + 1/cos2x = 1-2sin2x/1-sin2x
c) (cosx+sinx/cosx-sinx) - (cosx-sinx/cosx+sinx) = 2tan 2x
d) sin2x/1+cos2x = tanx
e)
a/ \(sin3x=sin\left(2x+x\right)=sin2xcosx+cos2x.sinx\)
\(=2sinxcos^2x+\left(1-2sin^2x\right)sinx=2sinx\left(1-sin^2x\right)+sinx-2sin^3x\)
\(=3sinx-4sin^3x\)
b/
\(tan2x+\frac{1}{cos2x}=\frac{sin2x}{cos2x}+\frac{1}{cos2x}=\frac{sin2x+1}{cos2x}=\frac{2sinxcosx+sin^2x+cos^2x}{cos^2x-sin^2x}\)
\(=\frac{\left(sinx+cosx\right)^2}{\left(sinx+cosx\right)\left(cosx-sinx\right)}=\frac{sinx+cosx}{cosx-sinx}=\frac{\left(sinx+cosx\right)\left(cosx-sinx\right)}{\left(cos-sinx\right)^2}\)
\(=\frac{cos^2x-sin^2x}{cos^2x+sin^2x-2sinxcosx}=\frac{1-2sin^2x}{1-sin2x}\)
c/
\(\frac{cosx+sinx}{cosx-sinx}-\frac{cosx-sinx}{cosx+sinx}=\frac{\left(cosx+sinx\right)^2-\left(cosx-sinx\right)^2}{cos^2x-sin^2x}\)
\(=\frac{2sinxcosx+2sinxcosx}{cos2x}=\frac{4sinxcosx}{cos2x}=\frac{2sin2x}{cos2x}=2tan2x\)
d/
\(\frac{sin2x}{1+cos2x}=\frac{2sinxcosx}{1+2cos^2x-1}=\frac{2sinxcosx}{2cos^2x}=\frac{sinx}{cosx}=tanx\)
e/