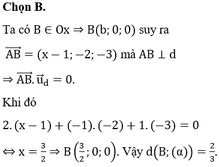Cho điểm A thuộc đường thẳng d -2x+y+2=0 và điểm b(1;-1),c(3;-1) tìm toạ độ điểm A thoả mãn để tam giác ABC cân tai A
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
NH
Những câu hỏi liên quan
Cho đường thẳng (d) : y = - 2x + 1
a. Điểm nào sau đây thuộc (d):: M(– 1; 3) ; N(1 ; 1) ; K(- 1 /2 ; 0)
b. Tìm toạ độ điểm E thuộc (d)biết Xe = – 2
c.Tìm toạ độ điểm F thuộc(d) biết Yf = 3
d. Cho điểm A( m – 1; 2) thuộc (d) . Tính m ?
b: Thay x=-2 vào (d), ta được:
y=4+1=5
Đúng 1
Bình luận (0)
cho 2 điểm A(-2;2), B(4;-6) và đường thẳng \(\Delta:2x-y+1=0\). tìm điểm M thuộc \(\Delta\) để M cách đều 2 điểm A,B
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(1;2;3) và đường thẳng (d):
x
-
2
2
y
+
2
-
1
z
-
3
1
. Gọi điểm B thuộc trục Ox sao cho AB vuông góc với đường thẳng (d). Khoảng cách từ B đ...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(1;2;3) và đường thẳng (d): x - 2 2 = y + 2 - 1 = z - 3 1 . Gọi điểm B thuộc trục Ox sao cho AB vuông góc với đường thẳng (d). Khoảng cách từ B đến mặt phẳng ( α ): 2x+2y-z-1=0 là:
A. 2
B. 2 3
C. 1 3
D. 1
Cho điểm A (1; 1), tồn tại điểm B thuộc đường thẳng d: 2x + 3y + 4 = 0 sao cho đường thẳng d và đường thẳng AB hợp với nhau một góc 45 độ. Biết điểm B có tung độ âm, hoành độ điểm B là ?
d nhận \(\left(2;3\right)\) là 1 vtpt nên nhận \(\overrightarrow{u}=\left(3;-2\right)\) là 1 vtcp
Do \(B\in d\) nên tọa độ có dạng: \(B\left(b;\dfrac{-2b-4}{3}\right)\Rightarrow\overrightarrow{AB}=\left(b-1;\dfrac{-2b-7}{3}\right)\)
\(cos45^0=\dfrac{\left|3.\left(b-1\right)+\dfrac{2\left(2b+7\right)}{3}\right|}{\sqrt{3^2+2^2}.\sqrt{\left(b-1\right)^2+\left(\dfrac{2b+7}{3}\right)^2}}=\dfrac{1}{\sqrt{2}}\)
\(\Leftrightarrow2\left(13b+5\right)^2=13\left(13b^2+10b+58\right)\)
\(\Leftrightarrow169b^2+130b-704=0\Rightarrow\left[{}\begin{matrix}b=-\dfrac{32}{13}\\b=\dfrac{22}{13}\Rightarrow y_B=-\dfrac{32}{13}< 0\left(loại\right)\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho 2 điểm P(1;6) và Q(-3;-4) và đường thẳng △: 2x - y - 1 = 0. Tọa độ điểm M thuộc △ sao cho MP + MQ nhỏ nhất.
A. M(0;-1)
B. M(2;3)
C. M(1;1)
D. M(3;5)
Thay tọa độ P, Q vào phương trình \(\Delta\) ta được 2 giá trị cùng dấu \(\Rightarrow\) P, Q nằm cùng phía so với \(\Delta\)
Gọi A là điểm đối xứng với \(P\) qua \(\Delta\Rightarrow AM=PM\)
\(\Rightarrow MP+MQ=AM+MQ\ge AQ\)
Dấu "=" xảy ra khi và chỉ khi A, M, Q thẳng hàng hay M là giao điểm AQ và \(\Delta\)
Phương trình đường thẳng d qua P và vuông góc \(\Delta\) có dạng:
\(1\left(x-1\right)+2\left(y-6\right)=0\Leftrightarrow x+2y-13=0\)
Tọa độ giao điểm H giữa d và \(\Delta\) là nghiệm: \(\left\{{}\begin{matrix}2x-y-1=0\\x+2y-13=0\end{matrix}\right.\) \(\Rightarrow H\left(3;5\right)\)
A đối xứng P qua \(\Delta\) khi và chỉ khi H là trung điểm AP \(\Rightarrow A\left(5;4\right)\)
\(\Rightarrow\overrightarrow{QA}=\left(8;8\right)=8\left(1;1\right)\Rightarrow\) đường thẳng AQ nhận (1;-1) là 1 vtpt
Phương trình AQ:
\(1\left(x+3\right)-1\left(y+4\right)=0\Leftrightarrow x-y-1=0\)
Tọa độ M là nghiệm: \(\left\{{}\begin{matrix}x-y-1=0\\2x-y-1=0\end{matrix}\right.\) \(\Rightarrow M\left(0;-1\right)\)
Đúng 0
Bình luận (0)
Câu 1. Cho tam giác ABC với A(1; 2), B(−2; 5) và C(0; 1). Gọi H, K lần lượt là chân đường cao kẻ từcác đỉnh A, B. Hãy chỉ ra một véc-tơ pháp tuyến của mỗi đường thằng AH, BK.Câu 2. Cho hai đường thẳng d1 : −3x + y − 2 0 và d2 : 2x − 3 0.a) Hãy chỉ ra một VTPT của d1, d2.b) Trong các điểm A(2; 0), B(−1; −1), C(frac{3}{2}; 1), D(frac{3}{2}; frac{13}{2}) điểm nào thuộc d1, điểm nào thuộc d2?Câu 3. Viết phương trình tổng quát của đường thẳng d biếta) d đi qua điểm A(−2; 5) và có VTPT −→n (−1; 2)....
Đọc tiếp
Câu 1. Cho tam giác ABC với A(1; 2), B(−2; 5) và C(0; 1). Gọi H, K lần lượt là chân đường cao kẻ từ
các đỉnh A, B. Hãy chỉ ra một véc-tơ pháp tuyến của mỗi đường thằng AH, BK.
Câu 2. Cho hai đường thẳng d1 : −3x + y − 2 = 0 và d2 : 2x − 3 = 0.
a) Hãy chỉ ra một VTPT của d1, d2.
b) Trong các điểm A(2; 0), B(−1; −1), C(\(\frac{3}{2}\); 1), D(\(\frac{3}{2}\); \(\frac{13}{2}\)) điểm nào thuộc d1, điểm nào thuộc d2?
Câu 3. Viết phương trình tổng quát của đường thẳng d biết
a) d đi qua điểm A(−2; 5) và có VTPT −→n = (−1; 2).
b) d đi qua điểm A(−5; 2) và vuông góc với đường thẳng BC biết tọa độ điểm B(1; 1) và
C(2; 3).
c) d đi qua điểm A(−1; 1) và song song với đường thẳng d': −4x − y + 2 = 0.
a.Tìm các giá trị của m để đường thẳng y = 2x - m2 - m đi qua điểm A(1 ; 0)
b.Tìm m để hai đường thẳng sau cắt nhau tại một điểm thuộc trục hoành:
(d): y = 2x + 4 và (d'): y = x + m - 2
a.
Để đường thẳng đi qua A
\(\Rightarrow2.1-m^2-m=0\Leftrightarrow m^2+m-2=0\)
\(\Rightarrow\left[{}\begin{matrix}m=1\\m=-2\end{matrix}\right.\)
b.
Hoành độ giao điểm của (d) với trục hoành:
\(2x+4=0\Rightarrow x=-2\Rightarrow\) hai đường thẳng cắt nhau tại (-2;0)
(d') đi qua (-2;0) nên:
\(-2+m-2=0\Rightarrow m=4\)
Đúng 3
Bình luận (0)
Trong không gian Oxyz, cho điểm A(1;2;-1), đường thẳng d:
x
-
1
2
y
+
1
1
z
-
2
-
1
và mặt phẳng (P):x+y+2z+10. Điểm B thuộc mặt phẳng (P) thỏa mãn đường thẳng AB vuông góc và cắt đường thẳng...
Đọc tiếp
Trong không gian Oxyz, cho điểm A(1;2;-1), đường thẳng d: x - 1 2 = y + 1 1 = z - 2 - 1 và mặt phẳng (P):x+y+2z+1=0. Điểm B thuộc mặt phẳng (P) thỏa mãn đường thẳng AB vuông góc và cắt đường thẳng d. Tọa độ điểm B là
A. (3;-2;-1)
B. (-3;8;-3)
C. (0;3;-2)
D. (6;-7;0)
Câu 29: Điểm thuộc đường thẳng y 4x - 2 là:A. (0; 2) B . (3; 1) C. (2; 6) D. (1; 6).Câu 30: Đồ thị của hàm số y 2x + 3 là đường thẳng đi qua hai điểm phân biệt sauA. (0; 3) và (3; 0) C. (0; 3) và (1,5; 2)C. (0; 3) và (1; 5) D. (3; 0) và (1,5; 0)Câu 31: Đồ thị của hàm số y ax + b (a ≠ 0) làmột đường cong Parabol.một đường thẳng đi qua hai điểm (0; b) và ((-b)/a;0)một đường thẳng đi qua gốc toạ độ.một đường thẳng đi qua hai điểm (b; 0) và (0; b)Câu 32: Khẳng định nào về hàm số...
Đọc tiếp
Câu 29: Điểm thuộc đường thẳng y = 4x - 2 là:
A. (0; 2) B . (3; 1) C. (2; 6) D. (1; 6).
Câu 30: Đồ thị của hàm số y = 2x + 3 là đường thẳng đi qua hai điểm phân biệt sau
A. (0; 3) và (3; 0) C. (0; 3) và (1,5; 2)
C. (0; 3) và (1; 5) D. (3; 0) và (1,5; 0)
Câu 31: Đồ thị của hàm số y = ax + b (a ≠ 0) là
một đường cong Parabol.
một đường thẳng đi qua hai điểm (0; b) và ((-b)/a;0)
một đường thẳng đi qua gốc toạ độ.
một đường thẳng đi qua hai điểm (b; 0) và (0; b)
Câu 32: Khẳng định nào về hàm số y = x + 3 là sai
A. Cắt Oy tại (0; 3) B. Nghịch biến trên
C. Cắt Ox tại (-3; 0) D. Đồng biến trên
Câu 33: Góc tạo bởi đường thẳng: y =\(\sqrt{3x+1}\) với trục Ox bằng
A. 300 B . 300 C. 450 D. 600.
Cho đường thẳng d : 2x + y -4 = 0 và A(4;1), B(1;-6). Tìm điểm M thuộc d thỏa mãn MA + MB nhỏ nhất