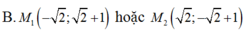Thay tọa độ P, Q vào phương trình \(\Delta\) ta được 2 giá trị cùng dấu \(\Rightarrow\) P, Q nằm cùng phía so với \(\Delta\)
Gọi A là điểm đối xứng với \(P\) qua \(\Delta\Rightarrow AM=PM\)
\(\Rightarrow MP+MQ=AM+MQ\ge AQ\)
Dấu "=" xảy ra khi và chỉ khi A, M, Q thẳng hàng hay M là giao điểm AQ và \(\Delta\)
Phương trình đường thẳng d qua P và vuông góc \(\Delta\) có dạng:
\(1\left(x-1\right)+2\left(y-6\right)=0\Leftrightarrow x+2y-13=0\)
Tọa độ giao điểm H giữa d và \(\Delta\) là nghiệm: \(\left\{{}\begin{matrix}2x-y-1=0\\x+2y-13=0\end{matrix}\right.\) \(\Rightarrow H\left(3;5\right)\)
A đối xứng P qua \(\Delta\) khi và chỉ khi H là trung điểm AP \(\Rightarrow A\left(5;4\right)\)
\(\Rightarrow\overrightarrow{QA}=\left(8;8\right)=8\left(1;1\right)\Rightarrow\) đường thẳng AQ nhận (1;-1) là 1 vtpt
Phương trình AQ:
\(1\left(x+3\right)-1\left(y+4\right)=0\Leftrightarrow x-y-1=0\)
Tọa độ M là nghiệm: \(\left\{{}\begin{matrix}x-y-1=0\\2x-y-1=0\end{matrix}\right.\) \(\Rightarrow M\left(0;-1\right)\)