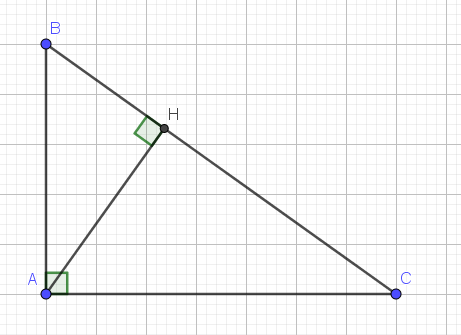
Xác định tung độ góc b. Biết đồ thị hàm số là y=3x+b a/cắt đường thẳng y=x+1 tại một điểm nằm trên trục tung
Bài 4: Đường thẳng song song và đường thẳng cắt nhau
Do đồ thị hàm số cắt đường thẳng y = x + 1 tại một điểm nằm trên trục tung nên b = 1
Đúng 0
Bình luận (0)
CỨu mình vớiiiiii
Cho (d): y= -2x+3 và
(d'):y= (2m+1)x-m+1.
Tìm m để (d) cắt (d') tại một điểm có tung độ bằng 2
Thay y=2 vào y=-2x+3, ta được:
\(-2x+3=2\)
=>\(-2x=2-3=-1\)
=>\(x=\dfrac{1}{2}\)
Thay \(x=\dfrac{1}{2};y=2\) vào y=(2m+1)x-m+1, ta được:
\(\dfrac{1}{2}\left(2m+1\right)-m+1=2\)
=>\(m+\dfrac{1}{2}-m+1=2\)
=>\(\dfrac{3}{2}=2\left(vôlý\right)\)
vậy: \(m\in\varnothing\)
Đúng 1
Bình luận (0)
Giúp mình với ạaaa
Cho hai hàm số bậc nhất
y=(2m-1)x+n+1
y=(5-m)x-1-n
Tìm m để đồ thị hai hàm số trên
a) cắt nhau
b)song song
c) trùng nhau
a: Đặt (d1): \(y=\left(2m-1\right)x+n+1\)
(d2): \(y=\left(5-m\right)x-1-n\)
Để (d1) cắt (d2) thì \(2m-1\ne5-m\)
=>\(3m\ne6\)
=>\(m\ne2\)
b: Để (d1)//(d2) thì \(\left\{{}\begin{matrix}2m-1=5-m\\n+1\ne-1-n\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3m=6\\2n\ne-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=2\\n\ne-1\end{matrix}\right.\)
c: Để \(\left(d1\right)\equiv\left(d2\right)\) thì \(\left\{{}\begin{matrix}2m-1=5-m\\n+1=-n-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3m=6\\2n=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=2\\n=-1\end{matrix}\right.\)
Đúng 2
Bình luận (0)
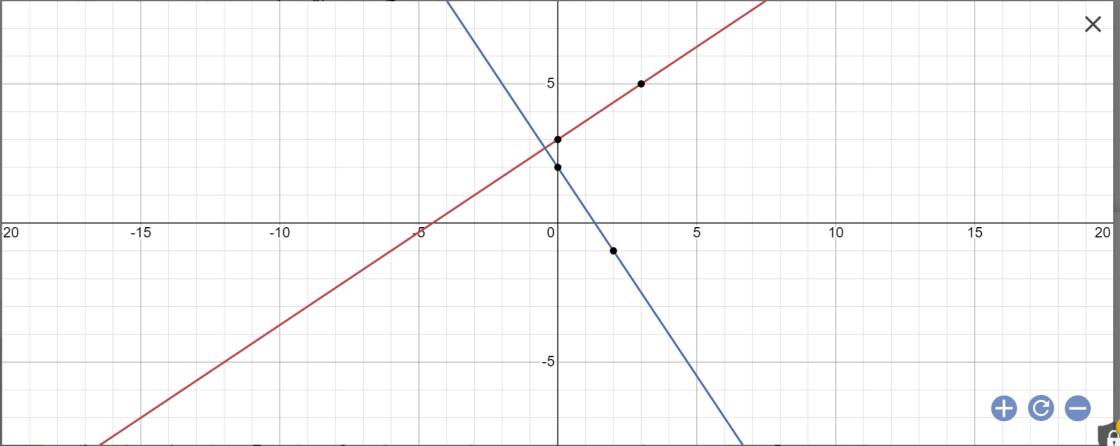
Vẽ đồ thị của các hàm số sau trên cùng một mặt phẳng tọa độ: y=⅔x+3 ; y=-³/²x+2
Bảng giá trị:
| x | -1 | 0 | 1 |
| \(y=\dfrac{2}{3}x+3\) | \(\dfrac{7}{3}\) | 3 | \(\dfrac{11}{3}\) |
| \(y=-\dfrac{3}{2}x+2\) | \(\dfrac{7}{2}\) | 2 | \(\dfrac{1}{2}\) |
Vẽ đồ thị:
Đúng 1
Bình luận (0)
Cho hai hàm số bậc nhất y=2x+3k và y=(2m+1)x+2k-3. Tìm đk đối với m và k để đồ thị của hai hàm số là: a) Hai đường thẳng cắt nhau. b) Hai đường thẳng song song với nhau. c) Hai đường thẳng trùng nhau
a: Để hai đường thẳng này cắt nhau thì \(2m+1< >2\)
=>\(2m\ne1\)
=>\(m\ne\dfrac{1}{2}\)
b: Để hai đường thẳng này song song thì \(\left\{{}\begin{matrix}2m+1=2\\2k-3\ne3k\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2m=1\\-k\ne3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{1}{2}\\k\ne-3\end{matrix}\right.\)
c: Để hai đường thẳng này trùng nhau thì \(\left\{{}\begin{matrix}2m+1=2\\2k-3=3k\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2m=1\\-k=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{1}{2}\\k=-3\end{matrix}\right.\)
Đúng 2
Bình luận (0)
viết phương trình đường thẳng song song với đường thẳng 2x - y = 5 và đi qua điểm (1;3)
Gọi (d): y = ax + b (a ≠ 0) là phương trình đường thẳng cần viết
Do (d) song song với đường thẳng 2x - y = 5 nên a = 2
⇒ (d): y = 2x + b
Do (d) đi qua điểm (1; 3) nên thay x = 1; y = 3 vào (d) ta có:
2.1 + b = 3
⇔ b = 3 - 2
⇔ b = 1
Vậy (d): y = 2x + 1
Đúng 5
Bình luận (0)
Cho đường thẳng △ : y = (m^2 -3)x - m + 1 với m là tham số. Tìm m để △ cắt đường thẳng d3 : y = -2x tại điểm có hoành độ bằng 2
Thay x=2 vào y=-2x, ta được:
\(y=-2\cdot2=-4\)
Thay x=2 và y=-2 vào \(y=\left(m^2-3\right)x-m+1\), ta được:
\(2\left(m^2-3\right)-m+1=-2\)
=>\(2m^2-6-m+1+2=0\)
=>\(2m^2-m-3=0\)
=>\(2m^2-3m+2m-3=0\)
=>(2m-3)(m+1)=0
=>\(\left[{}\begin{matrix}2m-3=0\\m+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{3}{2}\\m=-1\end{matrix}\right.\)
Đúng 1
Bình luận (0)
cho (d) : y=2x-1 (d') :y=x+1 A) vẽ (d) và (d') trên cùng mặt phẳng oxy B) tìm tọa độ giao điểm của (d) và (d')
a) Ta có: (d) \(y=2x-1\)
Hàm số cắt: \(Ox\left(\dfrac{1}{2};0\right);Oy\left(0;-1\right)\)
(d') \(y=x+1\)
Hàm số cắt: \(Ox\left(-1;0\right);Oy\left(0;1\right)\)
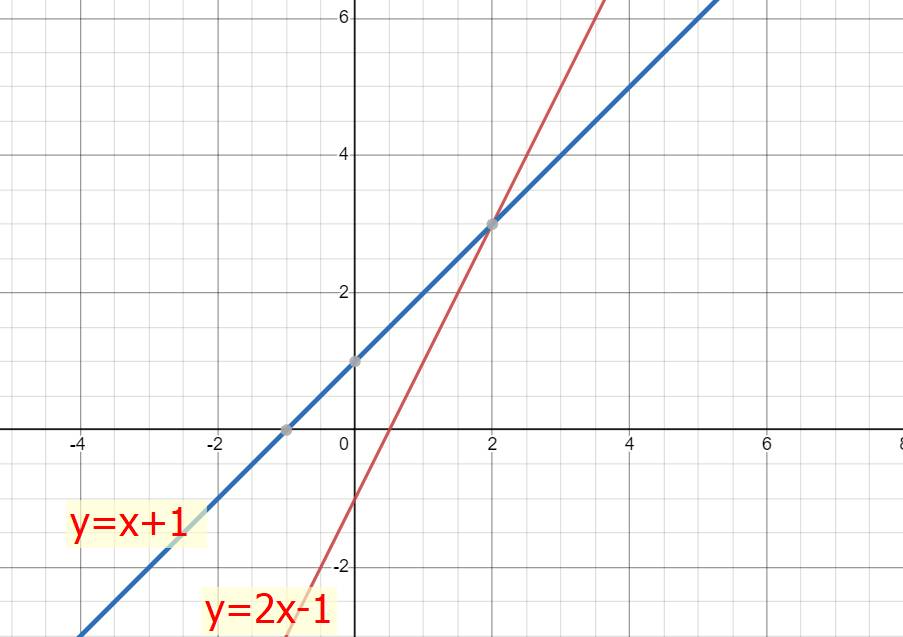
b) Phương trình hoành độ giao điểm cùa (d) và (d')
\(x+1=2x-1\)
\(\Leftrightarrow2x-x=1+1\)
\(\Leftrightarrow x=2\)
Thay x = 2 vào (d) ta có:
\(y=2\cdot2-1=3\)
Vậy tọa độ giao điểm của (d) và (d') là \(A\left(2;3\right)\)
Đúng 2
Bình luận (0)
viết phương trình đường thẳng d1 vuông góc d2 và cắt (d3) y=2x+1 tại tung độ =5
d2 là đường thẳng nào vậy bạn?
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A , Đường cao AH; biết HB = 3cm , HC = 4cm . Tính AB, AH
Lời giải:
a.
Áp dụng hệ thức lượng trong tam giác vuông ta có:
$AH^2=BH.CH=3.4=12$
$\Rightarrow AH=\sqrt{12}=2\sqrt{3}$ (cm)
$AB^2=BH.BC=BH(BH+CH)=3(3+4)=21$
$\Rightarrow AB=\sqrt{21}$ (cm)
Đúng 0
Bình luận (0)