chứng minh rằng: x-x2-1<0 với mọi số thực thuộc x
KL
Những câu hỏi liên quan
Bài 1: Chứng minh rằng hai phân thức sau bằng nhau
a)x2+2x+1/x2+x=x+1/x
b)x-3/x=x2-4x+3/x2-x
a) Ta có: \(\dfrac{x^2+2x+1}{x^2+x}\)
\(=\dfrac{\left(x+1\right)^2}{x\left(x+1\right)}\)
\(=\dfrac{x+1}{x}\)
b) Ta có: \(\dfrac{x^2-4x+3}{x^2-x}\)
\(=\dfrac{\left(x-1\right)\left(x-3\right)}{x\left(x-1\right)}\)
\(=\dfrac{x-3}{x}\)
Đúng 1
Bình luận (0)
cho x/z = z/y. chứng minh rằng (x2 + z2)/(y2 + z2) = x/ycho x/z = z/y. chứng minh rằng (x2 + z2)/(y2 + z2) = x/y
chứng minh rằng x2>2(x-1) với mọi số thực x
x2 > 2( x - 1 )
<=> x2 - 2x + 2 > 0
<=> ( x2 - 2x + 1 ) + 1 > 0
<=> ( x - 1 )2 + 1 > 0 ( luôn đúng ∀ x ∈ R )
Vậy bđt ban đầu được chứng minh
Đúng 1
Bình luận (0)
Chứng minh rằng x2 – x + 1 > 0 với mọi số thực x
Ta có:
\(x^2-x+1\)
\(=x^2-2\cdot\dfrac{1}{2}\cdot x+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\)
Mà: \(\left(x-\dfrac{1}{2}\right)^2\ge0\forall x\) và \(\dfrac{3}{4}>0\)
Nên: \(x^2-x+1>0\)
Đúng 2
Bình luận (0)
\(x^2-x+1\)
\(=x^2-\dfrac{1}{2}.x-\dfrac{1}{2}.x+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=x\left(x-\dfrac{1}{2}\right)-\dfrac{1}{2}\left(x-\dfrac{1}{2}\right)+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)\left(x-\dfrac{1}{2}\right)+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\) với mọi x ( đpcm )
Đúng 1
Bình luận (0)
\(x^2-x+1=x^2-2.x.\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\\ Mà:\left(x-\dfrac{1}{2}\right)^2>0\forall x\in R\\ Vậy:\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\in R\\ Vậy:x^2-x+1>0\forall x\in R\)
Đúng 2
Bình luận (0)
Chứng minh rằng: x 2 + 2 y 2 + 2 x y + 1 > 0 ; ∀ x , y
4. Tìm giá trị lớn nhất của các biểu thức a. A = 5 – 8x – x2 b. B = 5 – x2 + 2x – 4y2 – 4y 5. a. Cho a2 + b2 + c2 = ab + bc + ca chứng minh rằng a = b = c b. Tìm a, b, c biết a2 – 2a + b2 + 4b + 4c2 – 4c + 6 = 0 6. Chứng minh rằng: a. x2 + xy + y2 + 1 > 0 với mọi x, y b. x2 + 4y2 + z2 – 2x – 6z + 8y + 15 > 0 Với mọi x, y, z 7. Chứng minh rằng: x2 + 5y2 + 2x – 4xy – 10y + 14 > 0 với mọi x, y.
Cho x, y là hai số thực thỏa mãn
x
y
+
(
1
+
x
2
)
(
1
+
y
2
)
1.
Chứng minh rằng
x
1
+
y
2
+
y
1
+
x
2...
Đọc tiếp
Cho x, y là hai số thực thỏa mãn x y + ( 1 + x 2 ) ( 1 + y 2 ) = 1. Chứng minh rằng x 1 + y 2 + y 1 + x 2 = 0.
x y + ( 1 + x 2 ) ( 1 + y 2 ) = 1 ⇔ ( 1 + x ) 2 ( 1 + y ) 2 = 1 − x y ⇒ ( 1 + x 2 ) ( 1 + y 2 ) = 1 - x y 2 ⇔ 1 + x 2 + y 2 + x 2 y 2 = 1 − 2 x y + x 2 y 2 ⇔ x 2 + y 2 + 2 x y = 0 ⇔ x + y 2 = 0 ⇔ y = − x ⇒ x 1 + y 2 + y 1 + x 2 = x 1 + x 2 − x 1 + x 2 = 0
Đúng 0
Bình luận (0)
Chứng minh rằng không có số hữu tỉ nào thoả mãn: a) x2 = 7 b) x2 – 3x = 1 c) x + với x khác 1 và -1.
Chứng minh rằng biểu thức
Q
x
2
-
1
1
x
-
1
-
1
x
+
1
+
1
luôn dương với
x
≠
±
1
Đọc tiếp
Chứng minh rằng biểu thức Q = x 2 - 1 1 x - 1 - 1 x + 1 + 1 luôn dương với x ≠ ± 1
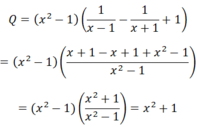
Do x2≥ 0 ∀ x ≠ ±1 nên Q=x2 + 1 ≥ 1 ∀ x ≠ ±1
Đúng 0
Bình luận (0)
Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của biến x:A (x - 1)(
x
2
+ x + 1) +
(
x
-
2
)
3
- 2(x + 1)(
x
2
- x +1) + 6
(
x
-...
Đọc tiếp
Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của biến x:
A = (x - 1)( x 2 + x + 1) + ( x - 2 ) 3 - 2(x + 1)( x 2 - x +1) + 6 ( x - 1 ) 2 .
Thực hiện khai triển hằng đẳng thức
A = ( x 3 – 1) + ( x 3 – 6 x 2 + 12x – 8) – 2( x 3 + 1) + 6( x 2 – 2x + 1).
Rút gọn A = -5 không phụ thuộc biến x.
Đúng 0
Bình luận (0)



