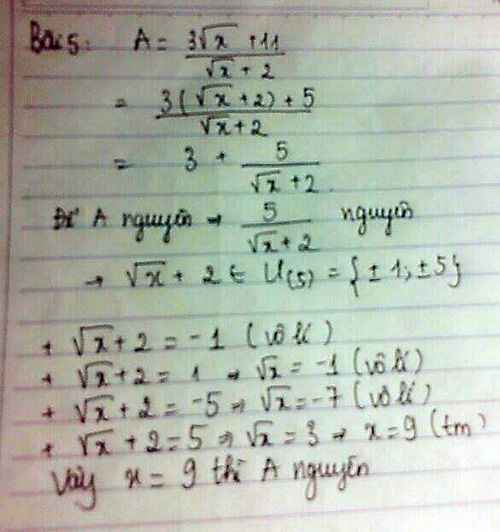cho số hữu tỉ \(P=\dfrac{x+2}{x-3}\) . Tìm x để P=0; P>0; P<0
GT
Những câu hỏi liên quan
Tìm x thuộc Z để \(\dfrac{3-x}{x+10}\)
a,là số hữu tỉ dương
b,là số hữu tỉ âm
c, bằng 0
a: x là số dương
=>(3-x)/(x+10)>0
=>(x-3)/(x+10)<0
=>-10<x<3
b: x<0
=>(3-x)/(x+10)>0
=>x>3 hoặc x<-10
c: x=0
=>3-x=0
=>x=3
Đúng 1
Bình luận (0)
Cho số hữu tỉ
x= \(\dfrac{a+5}{-12}\)
a, Khi a = -2 thì x là số hữu tỉ dương hay âm
b, Khi a= -9 thì x là số hữu tỉ dương hay âm
c , Tìm giác trị của a để x= 0
d, So sánh x với -1,8 khi a= -37
a) Khi a = -2 thì x = (-2 + 5)/(-12) = 3/(-12) = -1/4
Vậy x là số hữu tỉ âm
b) Khi a = -9 thì x = (-9 + 5)/(-12) = (-4)/(-12) = 1/3
Vậy x là số hữu tỉ dương
c) Để x = 0 thì a + 5 = 0
a = -5
d) Khi a = -37 thì
x = (-37 + 5)/(-12)
= (-32)/(-12)
= 8/3 > 0
Mà 0 > -1,8
Vậy x > -1,8 khi a = -37
Đúng 3
Bình luận (0)
a) Tìm số tự nhiên x sao cho: 2x+2x+3=72
b)Tìm x nguyên để số hữu tỉ \(\dfrac{x-2}{x+1}\) có giá trị nguyên
c) Tìm GTNN của biểu thức: P=|2x+7|+\(\dfrac{2}{5}\)
a) 2ˣ + 2ˣ⁺³ = 72
2ˣ.(1 + 2³) = 72
2ˣ.9 = 72
2ˣ = 72 : 9
2ˣ = 8
2ˣ = 2³
x = 3
b) Để số đã cho là số nguyên thì (x - 2) ⋮ (x + 1)
Ta có:
x - 2 = x + 1 - 3
Để (x - 2) ⋮ (x + 1) thì 3 ⋮ (x + 1)
⇒ x + 1 ∈ Ư(3) = {-3; -1; 1; 3}
⇒ x ∈ {-4; -2; 0; 2}
Vậy x ∈ {-4; -2; 0; 2} thì số đã cho là số nguyên
c) P = |2x + 7| + 2/5
Ta có:
|2x + 7| ≥ 0 với mọi x ∈ R
|2x + 7| + 2/5 ≥ 2/5 với mọi x ∈ R
Vậy GTNN của P là 2/5 khi x = -7/2
Đúng 1
Bình luận (0)
Tìm các số hữu tỉ x, biết :
a)\(\dfrac{-5}{x-3}\)<0
b)\(\dfrac{3-x}{x^2+1}\)≥0
c)\(\dfrac{\left(x-1\right)^2}{x-2}\)<0
\(a,\dfrac{-5}{x-3}< 0\Leftrightarrow x-3>0\left(-5< 0\right)\Leftrightarrow x>3\\ b,\dfrac{3-x}{x^2+1}\ge0\Leftrightarrow3-x\ge0\left(x^2+1>0\right)\Leftrightarrow x\le3\\ c,\dfrac{\left(x-1\right)^2}{x-2}< 0\Leftrightarrow x-2< 0\left[\left(x-1\right)^2\ge0\right]\Leftrightarrow x< 2\)
Đúng 2
Bình luận (0)
Tìm các số hữu tỉ x để \(\dfrac{3\sqrt{x}+11}{\sqrt{x}+2}\)là số nguyên
ĐK: \(x\ge0\)
\(A=\dfrac{3\sqrt{x}+11}{\sqrt{x}+2}\Leftrightarrow A\sqrt{x}+2A=3\sqrt{x}+11\)
\(\Leftrightarrow\left(A-3\right)\sqrt{x}=11-2A\left(1\right)\)
TH1: \(A=3\Rightarrow\) Không tồn tại x thỏa mãn.
TH2: \(A\ne3\)
\(\left(1\right)\Leftrightarrow\sqrt{x}=\dfrac{11-2A}{A-3}\ge0\)
\(\Rightarrow3< A\le\dfrac{11}{2}\)
Vậy \(3< A\le\dfrac{11}{2}\) thì \(A\in Z\).
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
a)Tìm 3 số hữu tỉ x sao cho: x.(x-1/3)<0
b)Tìm 2 số hữu tỉ x và y (y # 0) sao cho: x+y=x.y=x:y
a/ x.(x-1/3)<0
mà x > x-1/3
=> x>0 ; x-1/3 < 0
=> x>0 ; x<1/3
=> 0<x<1/3, x thuộc Q
chọn ba số x là : 1/4 ; 1/5; 1/6
b/
x+y = x.y= x:y
x+y = x.y
=> x= x.y-y = y.[x-1]
=> x:y= x-1 [1]
=> x+y = x:y = x-1
=> y= -1 thay vào [1]
=> x: [-1] = x-1
=> -x = x-1
=> 2x = 1
=> x= 1/2
Vậy x= 1/2 ; y= -1
Đúng 0
Bình luận (0)
a)x(x-1/3)<0
Do x>x-1/3
=>x>0 x-1/3<0
<=>0<x<1/3
=>0<x<4/12
=>x={1/12;2/12;3/12;...}
Bạn bảo tìm 3 số nên mk tìm nấy chứ có vô số x
b)xy=x:y
=>y.y=x:x=1
=>y=1 hoặc y=-1
*)y=1
=>x+1=x
<=>x-x=1
<=>0=1(L)
*)y=-1
=>x-1=-x
<=>x+x=1
<=>2x=1
<=>x=1/2
Vậy y=-1 x=1/2
Đúng 0
Bình luận (0)
a)Tìm 3 số hữu tỉ x sao cho: x.(x-1/3)<0
b)Tìm 2 số hữu tỉ x và y (y # 0) sao cho: x+y=x.y=x:y
a/ x.(x-1/3)<0
mà x > x-1/3
=> x>0 ; x-1/3 < 0
=> x>0 ; x<1/3
=> 0<x<1/3, x thuộc Q
chọn ba số x là : 1/4 ; 1/5; 1/6
b/
x+y = x.y= x:y
x+y = x.y
=> x= x.y-y = y.[x-1]
=> x:y= x-1 [1]
=> x+y = x:y = x-1
=> y= -1 thay vào [1]
=> x: [-1] = x-1
=> -x = x-1
=> 2x = 1
=> x= 1/2
Vậy x= 1/2 ; y= -1
Đúng 0
Bình luận (0)
Cho x, y, z là các số hữu tỉ khác 0 thoả mãn x+y=z
Cmr: \(A=\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}}\) là một số hữu tỉ.
Ta có: \(x+y=z\Rightarrow x=z-y\)
\(A=\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}}=\sqrt{\dfrac{x^2y^2+y^2z^2+x^2z^2}{x^2y^2z^2}}\)
\(=\sqrt{\dfrac{\left(z-y\right)^2y^2+y^2z^2+\left(z-y\right)^2z^2}{x^2y^2z^2}}\)
\(=\sqrt{\dfrac{y^4+y^2z^2-2y^3z+y^2z^2+z^4+y^2z^2-2yz^3}{x^2y^2z^2}}\)
\(=\sqrt{\dfrac{\left(y^4+2y^2z^2+z^4\right)-2yz\left(y^2+z^2\right)+y^2z^2}{x^2y^2z^2}}\)
\(=\sqrt{\dfrac{\left(y^2+z^2\right)^2-2yz\left(y^2+z^2\right)+y^2z^2}{x^2y^2z^2}}\)
\(=\sqrt{\dfrac{\left(y^2+z^2-yz\right)^2}{x^2y^2z^2}}=\left|\dfrac{y^2+z^2-yz}{xyz}\right|\)
Là một số hữu tỉ do x,y,z là số hữu tỉ
Đúng 0
Bình luận (0)
Tìm số hữu tỉ x để biểu thức P = \(\dfrac{x^2-4x}{x^2+2}\) có giá trị là một số nguyên dương.
Để P là số nguyên dương thì x^2-4x>=0 và x^2-4x chia hết cho x^2+2
=>x^2+2-4x-2 chia hết cho x^2+2 và (x>=4 hoặc x<=0)
=>-4x-2 chia hết cho x^2+2 và (x>=4 hoặc x<=0)
=>4x+2 chia hết cho x^2+2 và (x>=4 hoặc x<=0)
=>16x^2-4 chia hết cho x^2+2 và (x>=4 hoặc x<=0)
=>16x^2+32-36 chia hết cho x^2+2 và (x>=4 hoặc x<=0)
=>\(x^2+2\in\left\{2;3;4;6;9;12;18;36\right\}\) và (x>=4 hoặc x<=0)
=>\(x\in\left\{0;4;\sqrt{34};-\sqrt{34};-1;-\sqrt{2};-2;-\sqrt{7};-\sqrt{10};-4\right\}\)
Đúng 2
Bình luận (0)
Khi đề yêu cầu P nguyên mà ko có điều kiện x nguyên thì phương pháp tốt nhất luôn là tìm miền giá trị của P từ đó lọc ra những số nguyên rồi tìm ngược lại x
\(P=\dfrac{x^2-4x}{x^2+2}=\dfrac{-\left(x^2+2\right)+2x^2-4x+2}{x^2+2}=-1+\dfrac{2\left(x-1\right)^2}{x^2+2}\ge-1\)
\(P=\dfrac{2\left(x^2+2\right)-x^2-4x-4}{x^2+2}=2-\dfrac{\left(x+2\right)^2}{x^2+2}\le2\)
\(\Rightarrow-1\le P\le2\)
Mà \(P\) nguyên dương \(\Rightarrow P=\left\{1;2\right\}\)
- Với \(P=1\Rightarrow\dfrac{x^2-4x}{x^2+2}=1\Rightarrow-4x=2\Rightarrow x=-\dfrac{1}{2}\)
- Với \(P=2\Rightarrow\dfrac{x^2-4x}{x^2+2}=2\Rightarrow x^2+4x+4=0\Rightarrow x=-2\)
Vậy \(x=\left\{-2;-\dfrac{1}{2}\right\}\)
Đúng 1
Bình luận (0)