Cần gấp câu e,f
KG
Những câu hỏi liên quan
cần gấp ạ câu d , e , f, g, h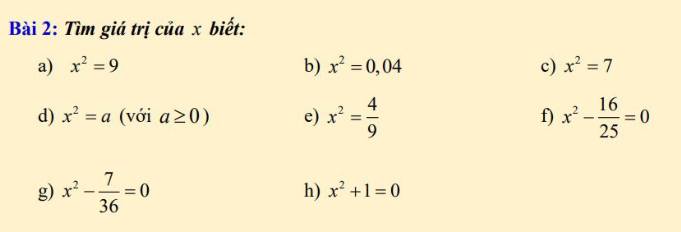
d) \(x^2=a\left(a\ge0\right)\)
\(\Rightarrow x=\sqrt{a}\)
e) \(x^2=\dfrac{4}{9}\)
\(\Rightarrow x^2=\left(\pm\dfrac{2}{3}\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-\dfrac{2}{3}\end{matrix}\right.\)
f) \(x^2-\dfrac{16}{25}=0\)
\(\Rightarrow x^2=\dfrac{16}{25}\)
\(\Rightarrow x^2=\left(\pm\dfrac{4}{5}\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{4}{5}\\x=-\dfrac{4}{5}\end{matrix}\right.\)
g) \(x^2-\dfrac{7}{36}=0\)
\(\Rightarrow x^2=\dfrac{7}{36}\)
\(\Rightarrow x^2=\left(\pm\sqrt{\dfrac{7}{36}}\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}x=\sqrt{\dfrac{7}{36}}\\x=-\sqrt{\dfrac{7}{36}}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{\sqrt{7}}{6}\\x=-\dfrac{\sqrt{7}}{6}\end{matrix}\right.\)
h) Ta có: \(x^2\ge0\forall x\)
\(\Rightarrow x^2+1\ge1>0\forall x\)
mà \(x^2+1=0\)
nên không tìm được giá trị nào của x thoả mãn đề bài.
Đúng 2
Bình luận (0)
Cần gấp đáp án bài 2 câu e;f và bài 3![]()

Cần gấp đáp án bài 2 câu e;f và bài 3
![]()

P=(2-5x)3x-(x+2)(x-2)
= 6x - 15x^2 - x^2 + 2^2
=6x - 16x^2 + 4
=2(3x - 8x^2 +2)
N=(x^2-3x-2)(x-1)-x(2x+1)
= x^3-3x^2-2x-x^2+3x+2-2x^2-x
=x^3-6x^2+2
=x^2(x-6)+2
Đúng 0
Bình luận (1)
Thay x=-4 vào P ta có
P=2(-12-128+2)
=2.-142
=-284
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giải giúp mk câu 1 a, b, c, d, e, f nha mik cần gấp
Em đưa cả ngữ liệu và đề bài đầy đủ lên đây để thầy cô và các bạn trong cộng đồng có thể hỗ trợ nhé!
Đúng 0
Bình luận (0)
Cần gấp câu f ạ
ĐK: \(x>0\)
\(P=\left(\dfrac{1}{\sqrt{x}}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right):\dfrac{\sqrt{x}}{x+\sqrt{x}}\)
\(=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}+\dfrac{x}{\sqrt{x}\left(\sqrt{x}+1\right)}\right).\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}}\)
\(=\dfrac{x+\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}.\left(\sqrt{x}+1\right)\)
\(=\dfrac{x+\sqrt{x}+1}{\sqrt{x}}=\sqrt{x}+\dfrac{1}{\sqrt{x}}+1\)
f, Áp dụng BĐT Cosi:
\(P=\sqrt{x}+\dfrac{1}{\sqrt{x}}+1\ge2\sqrt{\sqrt{x}.\dfrac{1}{\sqrt{x}}}+1=3\)
\(minP=3\Leftrightarrow x=1\)
Đúng 1
Bình luận (0)
a: Ta có: \(P=\left(\dfrac{1}{\sqrt{x}}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right):\dfrac{\sqrt{x}}{x+\sqrt{x}}\)
\(=\dfrac{x+\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}}\)
\(=\dfrac{x+\sqrt{x}+1}{\sqrt{x}}\)
b: Để P=-1 thì \(x+\sqrt{x}+1=-\sqrt{x}\)
\(\Leftrightarrow x+2\sqrt{x}+1=0\)
\(\Leftrightarrow\left(\sqrt{x}+1\right)^2=0\)(vô lý)
c: Thay \(x=16\) vào P, ta được:
\(P=\dfrac{16+4+1}{4}=\dfrac{21}{4}\)
Đúng 0
Bình luận (0)
mọi người giúp mik làm bài này với!!Đặt câu có sử dụng quan hệ từ hoặc cặp quan hệ từ sau : a. Vàb. Cònc. Nênd. Nếu…….thì……e. Vì ……nên…..f. Nhưngg. Củah. Đểmik đang cần gấp!!
Đọc tiếp
mọi người giúp mik làm bài này với!!
Đặt câu có sử dụng quan hệ từ hoặc cặp quan hệ từ sau :
a. Và
b. Còn
c. Nên
d. Nếu…….thì……
e. Vì ……nên…..
f. Nhưng
g. Của
h. Để
mik đang cần gấp!!
 giúp mik câu 2 f mik cần gấp
giúp mik câu 2 f mik cần gấp
Câu 2
a) (-105) + x = -217
x = -217 + 105
x = -112
b) x - 67 = -23
x = -23 + 67
x = 44
c) 4(3 - x) = 28
3 - x = 28 : 4
3 - x = 7
x = 3 - 7
x = -4
d) 5[x + (-81)] = 400
x - 81 = 400 : 5
x - 81 = 80
x = 80 + 81
x = 161
e) 140 : (x + 108) = 7
x + 108 = 140 : 7
x + 108 = 20
x = 20 - 108
x = -88
f) -27 + (-x) = -104
-27 - x = -104
x = -27 - (-104)
x = 77
Đúng 1
Bình luận (0)
Giúp mình làm mấy câu này với, mình đang cần gấp
d) 2x2 (x - y) + 2y(y - x)
e) 5a2b(a - 2b) - 2a(2b - a)
f) 4x2y(x - y) + 9xy2(x - y)
g) 50x2 (x - y)2 - 8y2 (y - x)2
Mình cần rất gấp nên mong các bạn giúp, xin cảm ơn
d. 2x2(x - y) + 2y(y - x)
= 2x2(x - y) - 2y(x - y)
= (2x2 - 2y)(x - y)
= 2(x2 - y)(x - y)
e. 5a2b(a - 2b) - 2a(2b - a)
= 5a2b(a - 2b) + 2a(a - 2b)
= (5a2b + 2a)(a - 2b)
= a(5ab + 2)(a - 2b)
f. 4x2y(x - y) + 9xy2(x - y)
= (4x2y + 9xy2)(x - y)
= xy(4x + 9y)(x - y)
g. 50x2(x - y)2 - 8y2(y - x)2
= 50x2(x2 - 2xy + y2) - 8y2(y2 - 2xy + x2)
= 50x2(x2 - 2xy + y2) - 8y2(x2 - 2xy + y2)
= 50x2(x - y)2 - 8y2(x - y)2
= (50x2 - 8y2)(x - y)2
= 2(25x2 - 4y2)(x - y)2.
Đúng 0
Bình luận (2)
g: Ta có: \(50x^2\left(x-y\right)^2-8y^2\left(y-x\right)^2\)
\(=2\left(x-y\right)^2\left(25x^2-4y^2\right)\)
\(=2\left(x-y\right)^2\left(5x-2y\right)\left(5x+2y\right)\)
Đúng 0
Bình luận (0)
giúp e giải gấp 2 câu này với ạ e cảm ơn vì hiện tại e cần gấp





