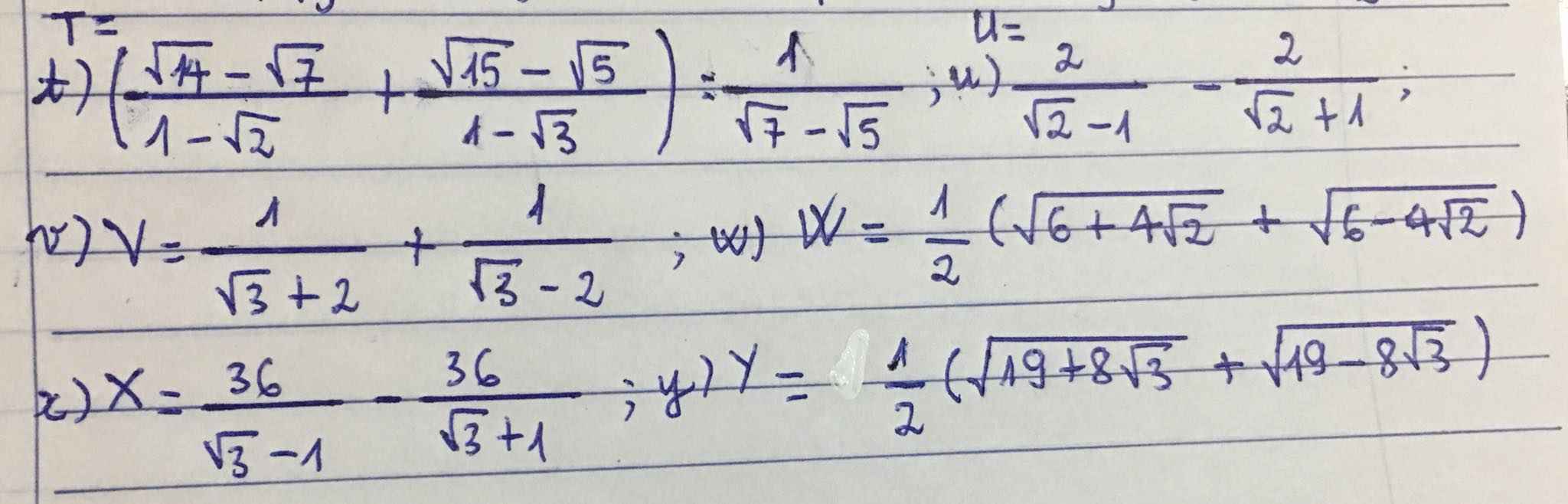ĐK: \(x>0\)
\(P=\left(\dfrac{1}{\sqrt{x}}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right):\dfrac{\sqrt{x}}{x+\sqrt{x}}\)
\(=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}+\dfrac{x}{\sqrt{x}\left(\sqrt{x}+1\right)}\right).\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}}\)
\(=\dfrac{x+\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}.\left(\sqrt{x}+1\right)\)
\(=\dfrac{x+\sqrt{x}+1}{\sqrt{x}}=\sqrt{x}+\dfrac{1}{\sqrt{x}}+1\)
f, Áp dụng BĐT Cosi:
\(P=\sqrt{x}+\dfrac{1}{\sqrt{x}}+1\ge2\sqrt{\sqrt{x}.\dfrac{1}{\sqrt{x}}}+1=3\)
\(minP=3\Leftrightarrow x=1\)
a: Ta có: \(P=\left(\dfrac{1}{\sqrt{x}}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right):\dfrac{\sqrt{x}}{x+\sqrt{x}}\)
\(=\dfrac{x+\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}}\)
\(=\dfrac{x+\sqrt{x}+1}{\sqrt{x}}\)
b: Để P=-1 thì \(x+\sqrt{x}+1=-\sqrt{x}\)
\(\Leftrightarrow x+2\sqrt{x}+1=0\)
\(\Leftrightarrow\left(\sqrt{x}+1\right)^2=0\)(vô lý)
c: Thay \(x=16\) vào P, ta được:
\(P=\dfrac{16+4+1}{4}=\dfrac{21}{4}\)





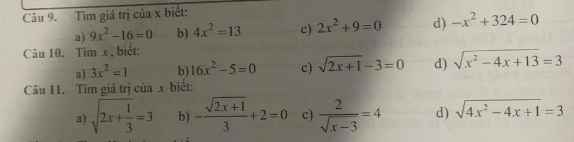

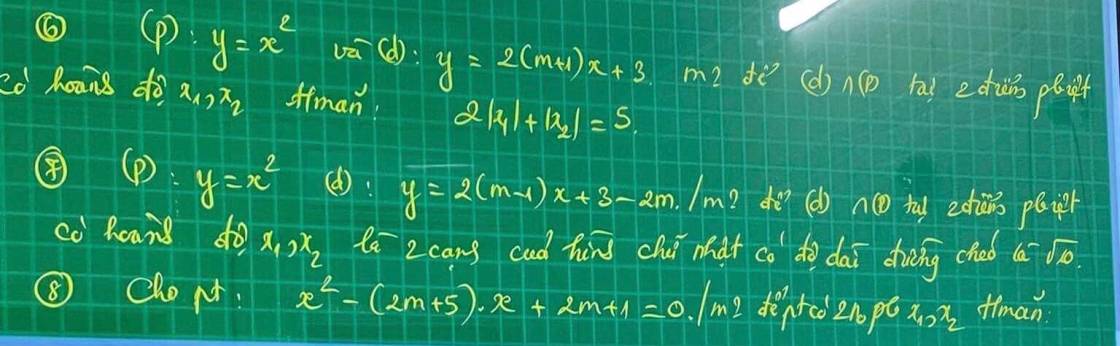

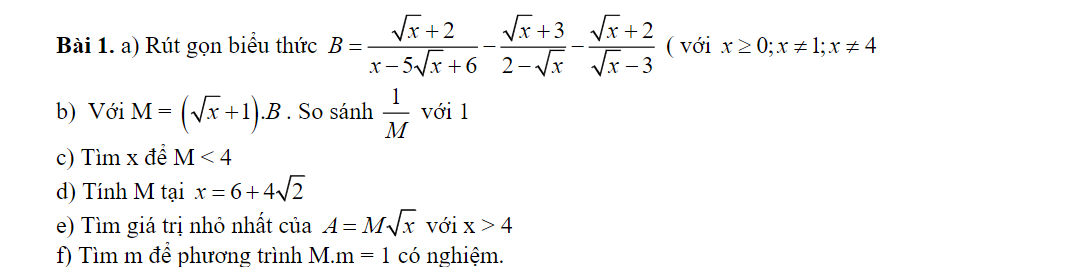 câu e và f cần giúp đỡ vs ạ
câu e và f cần giúp đỡ vs ạ