Dựng tam giác ABC, biết BC = 6 cm, \(\widehat{A}=40^o\) và đường cao AH = 4 cm.
SK
Những câu hỏi liên quan
(Bài 49 SGK toán 9 tr.87) Dựng tam giác ABC, biết BC = 6 cm, \(\widehat{A}=40^\circ\) và đường cao AH = 4cm.
Trình tự dựng gồm 3 bước:
- Dựng đoạn thẳng BC = 6cm
- Dựng cung chứa góc 40o trên đoạn thẳng BC.
- Dựng đường thẳng xy song song với BC và cách BC một khoảng là 4cm như sau:
Trên đường trung trực d của đoạn thẳng BC lấy đoạn HH' = 4cm (dùng thước có chia khoảng mm). Dựng đường thẳng xy vuông góc với HH' tại H
Gọi giao điểm xy và cung chứa góc là ,
. Khi đó tam giác ABC hoặc A'BC đều thỏa yêu cầu của đề toán

Cách dựng:
+ Dựng đoạn thẳng BC = 6cm.
+ Dựng cung chứa góc 40º trên đoạn thẳng BC (tương tự bài 46) :
Dựng tia Bx sao cho 
Dựng tia By ⊥ Bx.
Dựng đường trung trực của BC cắt By tại O.
Dựng đường tròn (O; OB).
Cung lớn BC chính là cung chứa góc 40º dựng trên đoạn BC.
+ Dựng đường thẳng d song song với BC và cách BC một đoạn 4cm:
Lấy D là trung điểm BC.
Trên đường trung trực của BC lấy D’ sao cho DD’ = 4cm.
Dựng đường thẳng d đi qua D’ và vuông góc với DD’.
+ Đường thẳng d cắt cung lớn BC tại A.
Ta được ΔABC cần dựng.
Chứng minh:
+ Theo cách dựng có BC = 6cm.
+ A ∈ cung chứa góc 40º dựng trên đoạn BC

+ A ∈ d song song với BC và cách BC 4cm
⇒ AH = DD’ = 4cm.
Vậy ΔABC thỏa mãn yêu cầu đề bài.
Biện luận: Do d cắt cung lớn BC tại hai điểm nên bài toán có hai nghiệm hình.

hình đây
Xem thêm câu trả lời
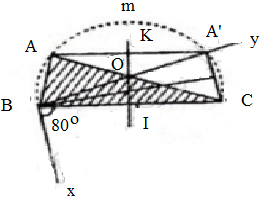
Dựng \(\Delta ABC\), biết BC = 6 cm, \(\widehat{BAC}=80^o,\) đường cao AH có độ dài là 2 cm.
Trình tự dựng gồm các bước sau:
- Dựng đoạn thẳng BC = 6cm
- Dựng cung chứa góc 80 trên đoạn thẳng BC (cung BmC).
- Trên đường vuông góc với BC tại I(I là trung điểm BC), chọn điểm K sao cho IK = 2cm. Từ K dựng đường thẳng vuông góc với IK. Đường thẳng này cắt cung chứa góc BmC tại A và A'.
ΔABC (hoặc ΔA'BC) là tam giác thỏa mãn yêu cầu đề bài.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A đường cao AH biết AB = 6 cm BC = 10 cm a) Tính độ dài đường cao AH và số đo B^ của tam giác ABC b) tính diện tích tam giác AHB
a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=10^2-6^2=64\)
=>\(AC=\sqrt{64}=8\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot10=6\cdot8=48\)
=>AH=48/10=4,8(cm)
Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}=\dfrac{4}{5}\)
nên \(\widehat{B}\simeq53^0\)
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2\)
=>\(BH\cdot10=6^2=36\)
=>BH=36/10=3,6(cm)
ΔAHB vuông tại H
=>\(S_{HAB}=\dfrac{1}{2}\cdot HA\cdot HB=\dfrac{1}{2}\cdot4,8\cdot3,6=8,64\left(cm^2\right)\)
Đúng 2
Bình luận (0)
a) Để tính độ dài đường cao \(AH\) và số đo \(\angle B\), chúng ta có thể sử dụng các quy tắc trong tam giác vuông.
Chúng ta biết rằng trong tam giác vuông, độ dài của đường cao \(AH\) từ đỉnh vuông \(A\) xuống cạnh huyền \(BC\) có thể được tính bằng công thức:
\[AH = \frac{1}{2} \times BC\]
Trong trường hợp này:
\[AH = \frac{1}{2} \times 10 \, \text{cm} = 5 \, \text{cm}\]
Số đo của góc \(\angle B\) có thể được tính bằng cách sử dụng hàm tan trong tam giác vuông:
\[\tan B = \frac{AH}{AB}\]
\[\angle B = \arctan\left(\frac{AH}{AB}\right)\]
Trong trường hợp này:
\[\tan B = \frac{5}{6}\]
\[\angle B = \arctan\left(\frac{5}{6}\right)\]
Bạn có thể sử dụng máy tính để tính toán giá trị chính xác của \(\angle B\).
b) Để tính diện tích tam giác \(AHB\), chúng ta sử dụng công thức diện tích tam giác:
\[S_{AHB} = \frac{1}{2} \times \text{độ dài } AH \times \text{độ dài } AB\]
Trong trường hợp này:
\[S_{AHB} = \frac{1}{2} \times 5 \, \text{cm} \times 6 \, \text{cm} = 15 \, \text{cm}^2\]
Vậy, độ dài của đường cao \(AH\) là \(5 \, \text{cm}\), số đo của góc \(\angle B\) có thể được tính, và diện tích tam giác \(AHB\) là \(15 \, \text{cm}^2\).
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AH24 cm và HC18 cm.
Tính: BH, ,BC,AC,AB và diện tích tam giác ABC
Bài 2: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB 12 cm và BC20 cm.
Tính: BH, ,AC,HC,AH và diện tích tam giác ABC
Bài 3: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB3 cm và AC4 cm.
Tính: BH, ,BC,HC,AH và diện tích tam giác ABC
Bài 4: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AC15 cm và AH 12 cm.
Tính: BH, ,BC,A...
Đọc tiếp
Bài 1: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AH=24 cm và HC=18 cm. Tính: BH, ,BC,AC,AB và diện tích tam giác ABC Bài 2: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB= 12 cm và BC=20 cm. Tính: BH, ,AC,HC,AH và diện tích tam giác ABC Bài 3: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB=3 cm và AC=4 cm. Tính: BH, ,BC,HC,AH và diện tích tam giác ABC Bài 4: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AC=15 cm và AH =12 cm. Tính: BH, ,BC,AB,AH và diện tích tam giác ABC Bài 5:Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB=20 cm và HC=9cm. Tính: BH, ,BC,AC,AH và diện tích tam giác ABC
Bài 5:
Ta có: \(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH\left(BH+9\right)=400\)
\(\Leftrightarrow BH^2+25HB-16HB-400=0\)
\(\Leftrightarrow BH=16\left(cm\right)\)
hay BC=25(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AC=15\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)
Đúng 3
Bình luận (0)
Cho tam giác ABC có AB = 6 cm, AC = 4,5 cm, BC = 7,5 cm
a) Chứng minh tam giác ABC vuông tại A. Tính các góc \(\widehat{B},\widehat{C}\) và đường cao AH của tam giác
b) Tìm tập hợp các điểm M sao cho \(S_{ABC}=S_{BMC}\)
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
Xét ΔABC vuông tại A có \(\sin B=\dfrac{AC}{BC}=\dfrac{4}{5}\)
nên \(\widehat{B}=53^0\)
=>\(\widehat{C}=37^0\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
hay AH=4,8(cm)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = 6 cm, AC = 4,5 cm, BC = 7,5 cm
a) Chứng minh tam giác ABC vuông tại A. Tính các góc \(\widehat{B},\widehat{C}\) và đường cao AH của tam giác
b) Tìm tập hợp các điểm M sao cho \(S_{ABC}=S_{BMC}\)
a. Ta có: AB2 = 62 = 36
AC2 = 4,52 = 20,25
BC2 = 7,52 = 56,25
Vì AB2 + AC2 = 36 + 20,25 = 56,25 = BC2 nên tam giác ABC vuông tại A (theo định lí đảo Pi-ta-go)
Kẻ AH ⊥ BC
Ta có: AH.BC = AB.AC
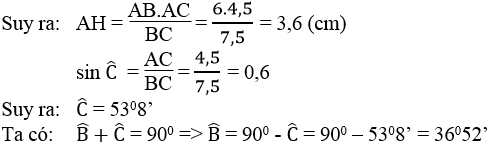 b. Tam giác ABC và tam giác MBC có chung cạnh đáy BC, đồng thời SABC = SMBC nên khoảng cách từ M đến BC bằng khoảng cách từ A đến BC. Vậy M thay đổi cách BC một khoảng bằng AH nên M nằm trên hai đường thẳng x và y song song với BC cách BC một khoảng bằng AH.
b. Tam giác ABC và tam giác MBC có chung cạnh đáy BC, đồng thời SABC = SMBC nên khoảng cách từ M đến BC bằng khoảng cách từ A đến BC. Vậy M thay đổi cách BC một khoảng bằng AH nên M nằm trên hai đường thẳng x và y song song với BC cách BC một khoảng bằng AH.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, kẻ đường cao AH và phân giác BE (H thuộc BC, E thuộc AC) Kẻ AD vuông góc BE ( D thuộc BE) a) CM ADHB nội tiếp trong 1 đường tròn. Xác định tâm O của đường tròn đób) CM widehat{EAD} widehat{HBD}và OD // HBc) biết góc ABC60 độ , và AB a ( a0) Tính theo a phần diện tích tam giác ABC nằm ngoài đường tròn O
Đọc tiếp
Cho tam giác ABC vuông tại A, kẻ đường cao AH và phân giác BE (H thuộc BC, E thuộc AC) Kẻ AD vuông góc BE ( D thuộc BE)
a) CM ADHB nội tiếp trong 1 đường tròn. Xác định tâm O của đường tròn đó
b) CM \(\widehat{EAD}\)= \(\widehat{HBD}\)và OD // HB
c) biết góc ABC=60 độ , và AB = a ( a>0) Tính theo a phần diện tích tam giác ABC nằm ngoài đường tròn O
Bài 1 Cho tam giác ABC vuông tại A có đường cao AH .biết BH = 9 cm ,HC = 16 cm .tính AH; AC ;số đo góc ABC (số đo góc làm tròn đến độ)
bài 2 Cho tam giác ABC vuông tại A , đường cao AH. biết AB = 3 cm ,AC = 4 cm. Tính độ dài các cạnh BC, AH và số đo góc ACB (làm tròn đến độ)
Bài 1:
AH=12cm
AC=20cm
\(\widehat{ABC}=37^0\)
Đúng 0
Bình luận (0)
cho một tam giác vuông abc vuông tại a ,đường cao ah . cho biết ab/ac =3/4 và ah=6 cm . tính bc, ch
giải hệ sau để tìm AB,AC
+1/AH^2=1/AB^2+1/AC^2
+AB^2 + AC^2 =BC^2
tìm đc AB,AC rùi thì Pitago là tìm đc BH,CH thôi
chúc thành công
Đúng 0
Bình luận (0)