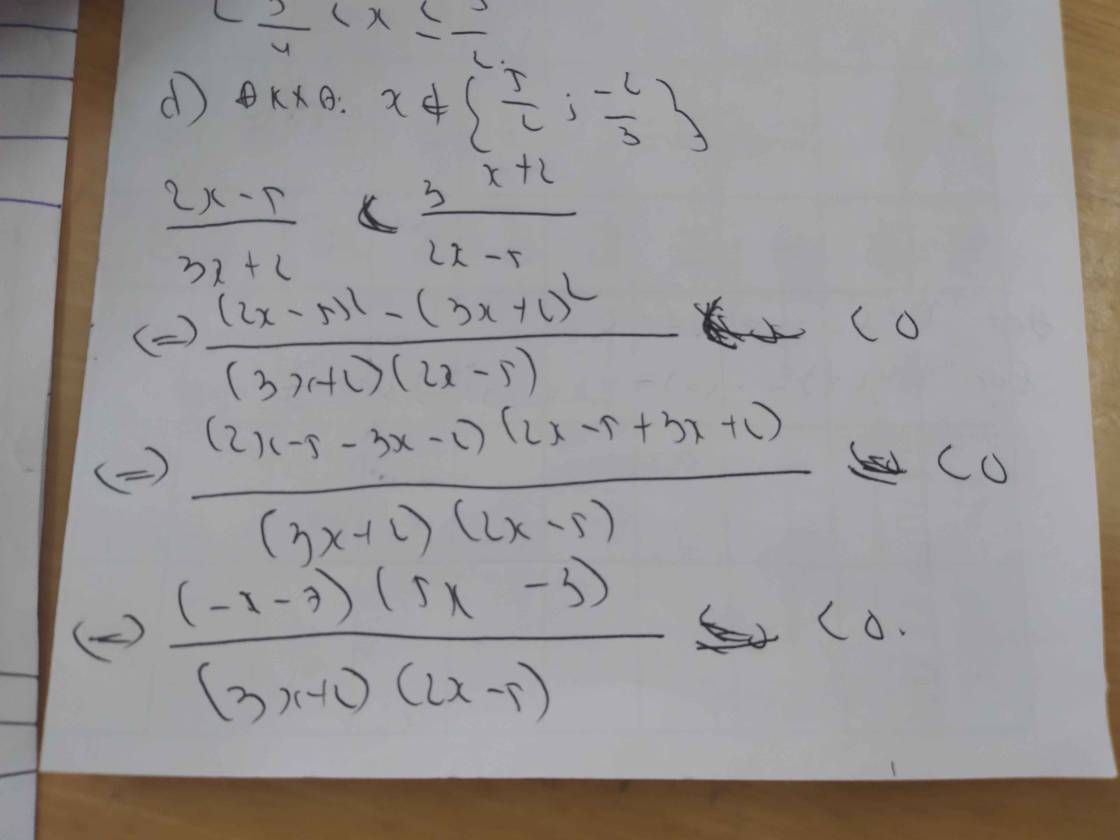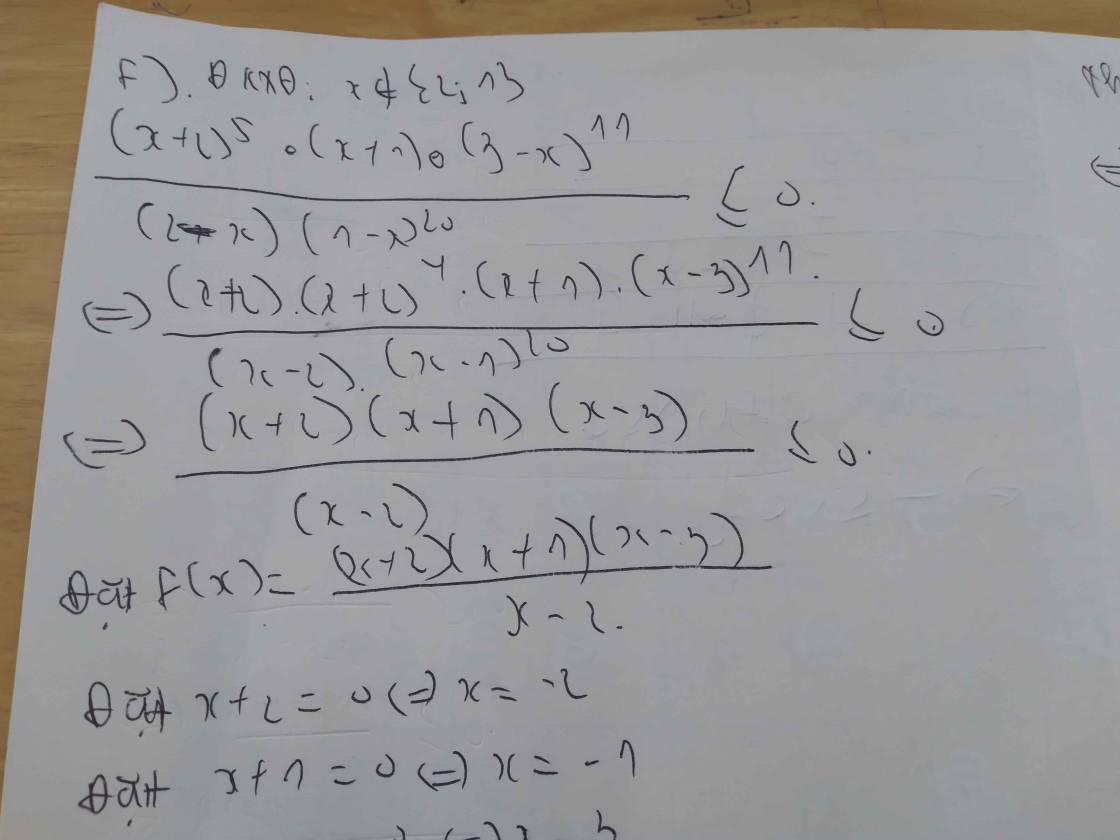Số dư của \(f\left(x\right)=-2x^5+70x^3-4x^2+x-1\) cho \(x-6\) là _______
PL
Những câu hỏi liên quan
a/Tìm số dư trong phép chia f(x)=1+x^2+x^4+x^6+...+x^100 : g(x) = (x+1)
b/tìm m để f(x)= 1+2m+x^2+x^4+x^6+...+x^100 : (x+1)
c/ Cm rằng : với m =571 thì f(x) = 2x^5 - 70x^3+4x^2 - x+1 chia hết cho x-6
GIÚP VỚI NHA! ĐANG CẦN GẤP! THANHKS MỌI NGƯỜI AHJHJ
a) \(g\left(x\right)=x+1=x-\left(-1\right)\)
Áp dụng định lý Bê-du có số dư của \(f\left(x\right)\)cho \(g\left(x\right)\)là :
\(f\left(-1\right)=1+\left(-1\right)^2+\left(-1\right)^4+....+\left(-1\right)^{100}\)
\(=1+1+1+...+1\)
( \(\frac{100-0}{2}+1=51\)số \(1\))
\(=51\)
Vậy ...
Đúng 0
Bình luận (0)
b) Thoạt trông khó nhưng rất đơn giản.
Tương tự phần a, áp dụng định lý Bê du có :
\(f\left(-1\right)=0\)
\(\Rightarrow51+2m=0\)
\(\Rightarrow m=-\frac{51}{2}\)
Vậy ....
c) Đề không rõ ràng.
Đúng 0
Bình luận (0)
Cho fleft(xright)x^2+2x^3-7x^5-9-6x^7+x^3+x^2+x^5-4x^2+3x^7
gleft(xright)x^5+2x^3-5x^8-x^7+x^3+4x^2-5x^7+x^4-4x^2-x^6-12
hleft(xright)x+4x^5-5x^6-x^7+4x^3+x^2-2x^7+x^6-4x^2-7x^7+x
a) Thu gọn và sắp xếp các đa thức trên theo lũy thừa tăng của biến
b) Tính fleft(xright)+gleft(xright)-hleft(xright)
Đọc tiếp
Cho \(f\left(x\right)=x^2+2x^3-7x^5-9-6x^7+x^3+x^2+x^5-4x^2+3x^7\)
\(g\left(x\right)=x^5+2x^3-5x^8-x^7+x^3+4x^2-5x^7+x^4-4x^2-x^6-12\)
\(h\left(x\right)=x+4x^5-5x^6-x^7+4x^3+x^2-2x^7+x^6-4x^2-7x^7+x\)
a) Thu gọn và sắp xếp các đa thức trên theo lũy thừa tăng của biến
b) Tính \(f\left(x\right)+g\left(x\right)-h\left(x\right)\)
a) Thu gọn, sắp xếp các đa thức theo lũy thừa tăng của biến
= -9 - 2x2 + 3x3 - 6x5 - 3x7
b) Tính -9 - 2x2 + 3x3 - 6x5 - 3x7 ) + (-12 + 3x3 + x4 + x5 - x6 - 6x7 - 5x8 ) - (2x - 3x2 + 4x3 +4x5 -4x6 - 10x7)
= - 9 - 2x2 + 3x3 - 6x5 - 3x7 -12 + 3x3 + x4 + x5 - x6 - 6x7 - 5x8 - 2x + 3x2 - 4x3 - 4x5 + 4x6 + 10x7
= -21 - 2x + x2 + 2x3 + x4 - 9x5 + 3x6 + x7 - 5x8
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của các biểu thức sauAx^2-4x+1 B4x^2+4x+11 Cleft(x-1right)left(x+3right)left(x+2right)left(x+6right)D2x^2+y^2-2xy+2x-4y+9 Tìm giá trị lớn nhất của các biểu thức sauE5-8x-x^2F4x-x^2+1
Đọc tiếp
Tìm giá trị nhỏ nhất của các biểu thức sau
A=\(x^2-4x+1\) \(B=4x^2+4x+11\)
\(C=\left(x-1\right)\left(x+3\right)\left(x+2\right)\left(x+6\right)\)
\(D=2x^2+y^2-2xy+2x-4y+9\)
Tìm giá trị lớn nhất của các biểu thức sau
\(E=5-8x-x^2\)
\(F=4x-x^2+1\)
Xét dấu f(x) biết:
1) f(x) = \(\left(3x^2-x-2\right)\left(4x^2-7x-2\right)\)
2) f(x) = \(\frac{2x^2-x-15}{3x-2}\)
3) f(x) = \(\frac{5}{2x-1}+\frac{3}{5-2x}\)
4) f(x) = \(\left(5-2x\right)^2\left(x+2\right)\)
5) f(x) = \(\frac{\left(x-1\right)^2\left(3-2x\right)}{x^2+x-6}\)
Cho hàm số yfleft(xright) có đạo hàm liên tục trên R, thỏa mãn: 2fleft(2xright)+fleft(1-2xright)12x^2. Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x1 là:A. y4x-2B. y2x+2C. y2x-6D. y4x-6
Đọc tiếp
Cho hàm số \(y=f\left(x\right)\) có đạo hàm liên tục trên R, thỏa mãn: \(2f\left(2x\right)+f\left(1-2x\right)=12x^2\). Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ \(x=1\) là:
A. \(y=4x-2\)
B. \(y=2x+2\)
C. \(y=2x-6\)
D. \(y=4x-6\)
Bài 1 Xét dấu biểu thức sau
1 , fleft(xright)2x^2-x+1
2 , fleft(xright)-2x^2+5x+7
3 , fleft(xright)9x^2-12x+4
4 , fleft(xright)2x^2+2x+5
5 , fleft(xright)2x^2+2sqrt{2}x+1
6 , fleft(xright)-4x^2-4x+1
7 , fleft(xright)sqrt{3}x+left(sqrt{3}+1right)x+1
8 , fleft(xright)x^2+left(sqrt{5}-1right)x-sqrt{5}
9 , fleft(xright)x^2-left(sqrt{7}-1right)+sqrt{3}
10 , fleft(xright)left(1-sqrt{2}right)x^2-2x+1+sqrt{2}
Đọc tiếp
Bài 1 Xét dấu biểu thức sau
1 , \(f\left(x\right)=2x^2-x+1\)
2 , \(f\left(x\right)=-2x^2+5x+7\)
3 , \(f\left(x\right)=9x^2-12x+4\)
4 , \(f\left(x\right)=2x^2+2x+5\)
5 , \(f\left(x\right)=2x^2+2\sqrt{2}x+1\)
6 , \(f\left(x\right)=-4x^2-4x+1\)
7 , \(f\left(x\right)=\sqrt{3}x+\left(\sqrt{3}+1\right)x+1\)
8 , \(f\left(x\right)=x^2+\left(\sqrt{5}-1\right)x-\sqrt{5}\)
9 , \(f\left(x\right)=x^2-\left(\sqrt{7}-1\right)+\sqrt{3}\)
10 , \(f\left(x\right)=\left(1-\sqrt{2}\right)x^2-2x+1+\sqrt{2}\)
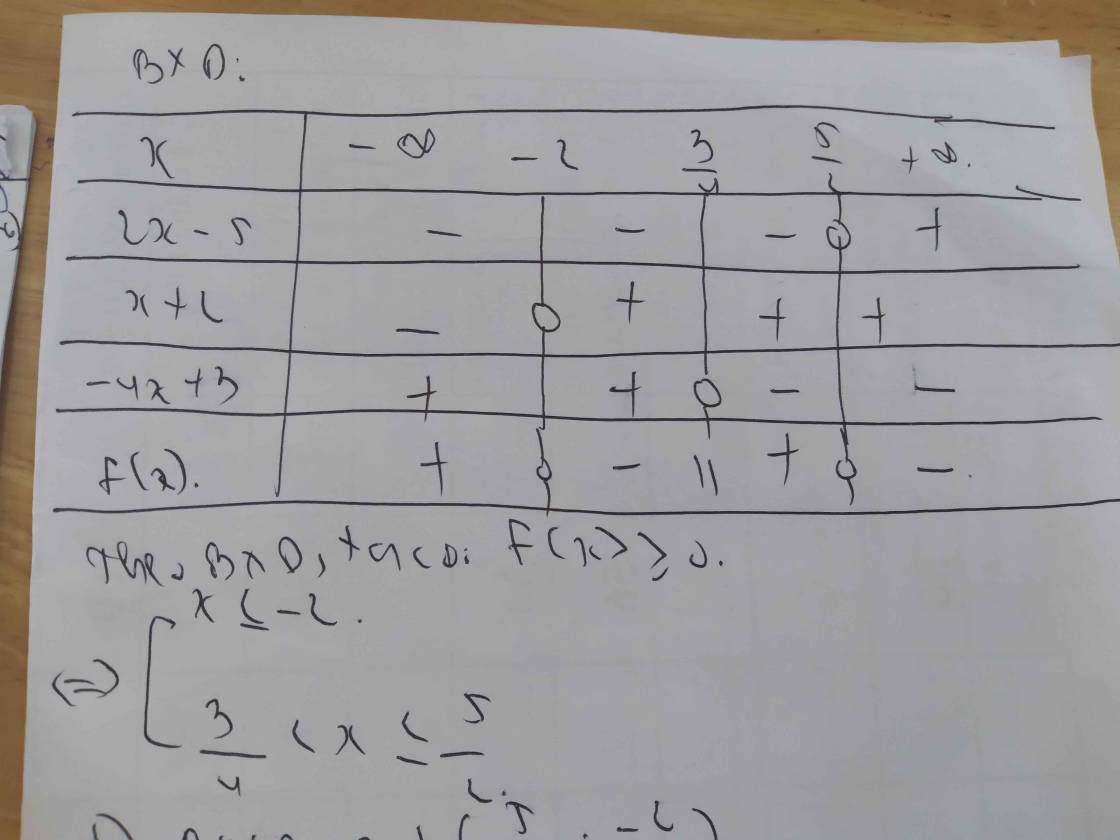
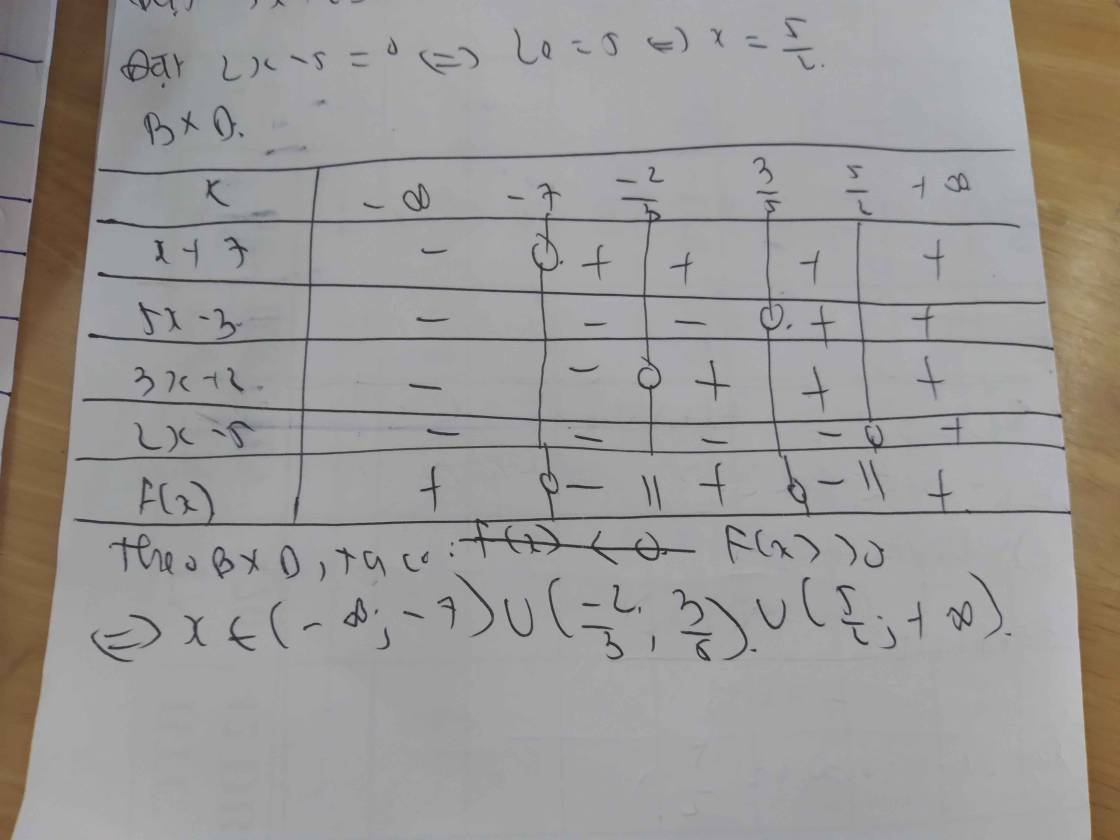
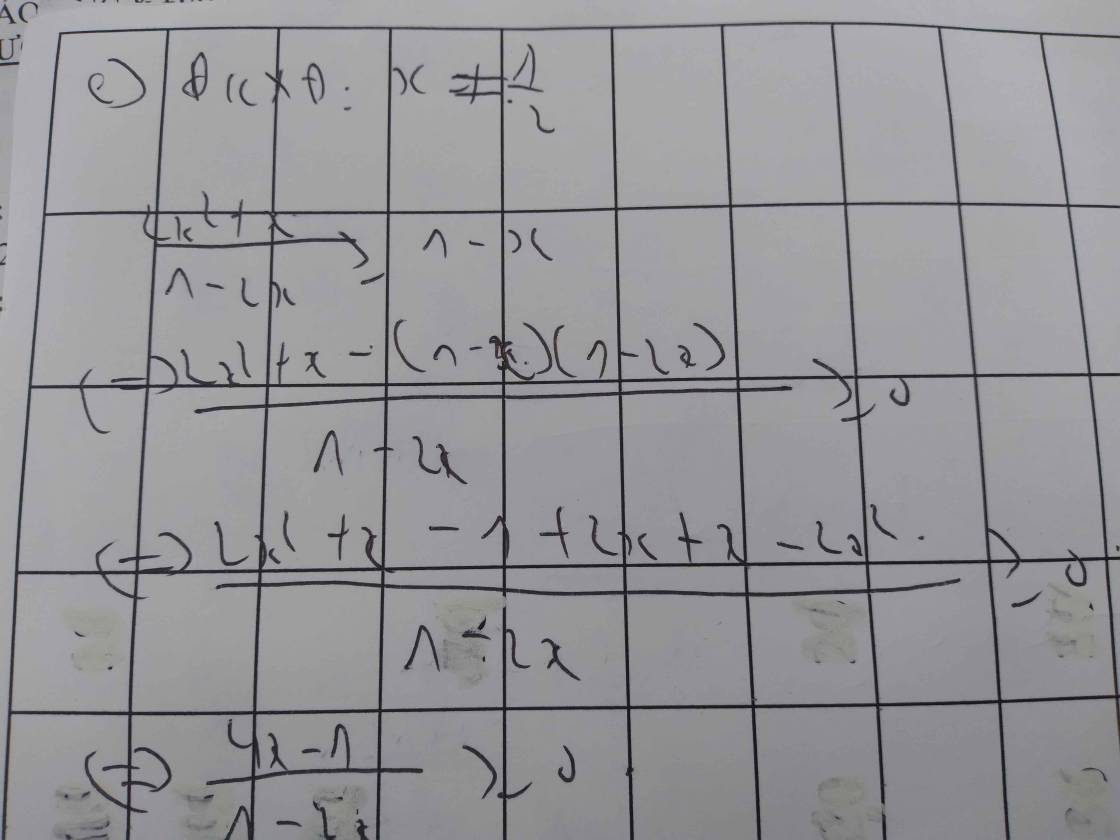
Giải các bất phương trình saua/ (x+1).(x-1).(3x-6)0b/ dfrac{x+3}{x-2}le0c/ dfrac{left(2x-5right).left(x+2right)}{-4x+3}ge0d/ dfrac{2x-5}{3x+2} dfrac{3x+2}{2x-5}e/ dfrac{2x^2+x}{1-2x}ge1-xf/ dfrac{left(2+xright)^5.left(x+1right).left(3-xright)^{11}}{left(2-xright).left(1-xright)^{20}}le0
Đọc tiếp
Giải các bất phương trình sau
a/ (x+1).(x-1).(3x-6)>0
b/ \(\dfrac{x+3}{x-2}\le0\)
c/ \(\dfrac{\left(2x-5\right).\left(x+2\right)}{-4x+3}\ge0\)
d/ \(\dfrac{2x-5}{3x+2}< \dfrac{3x+2}{2x-5}\)
e/ \(\dfrac{2x^2+x}{1-2x}\ge1-x\)
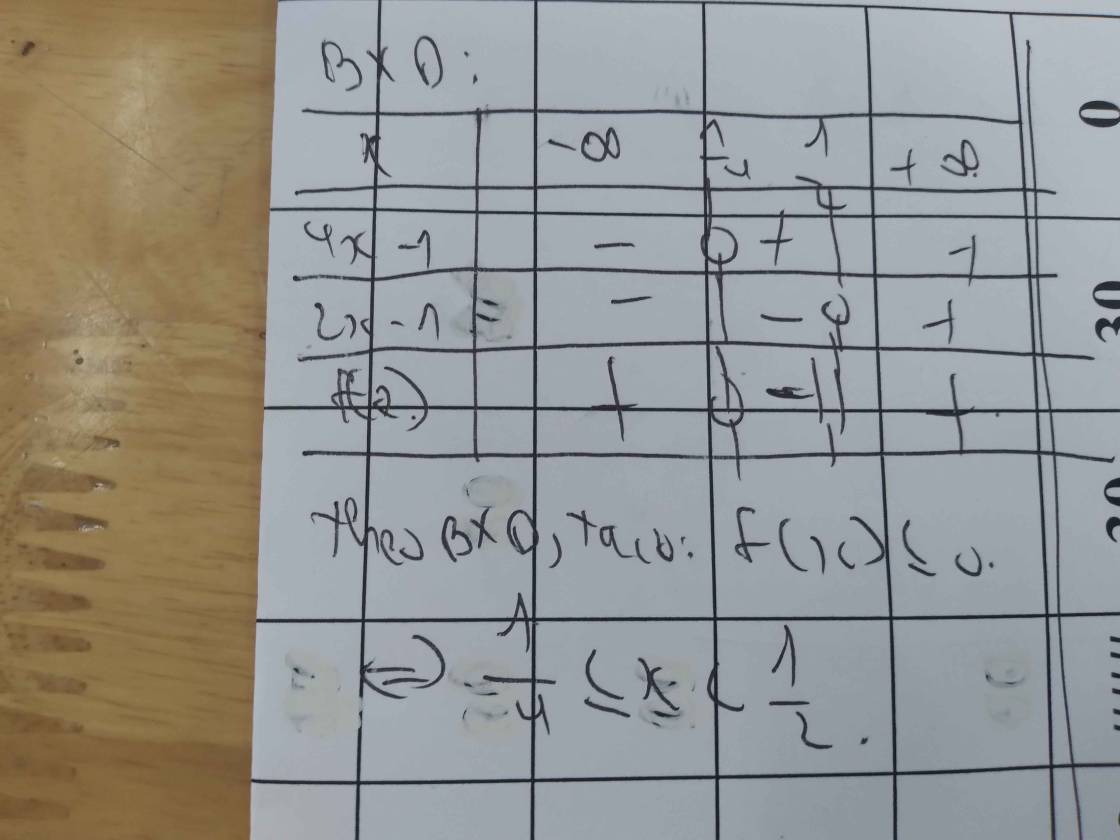
f/ \(\dfrac{\left(2+x\right)^5.\left(x+1\right).\left(3-x\right)^{11}}{\left(2-x\right).\left(1-x\right)^{20}}\le0\)
a) \(\left(x+1\right)\left(x-1\right)\left(3x-6\right)>0\)
Lập bảng xét dấu ta được kết quả :
\(Bpt\Leftrightarrow\left[{}\begin{matrix}-1< x< 1\\x>2\end{matrix}\right.\)
b) \(\dfrac{x+3}{x-2}\le0\)
Lập bảng xét dấu ta được kết quả :
\(Bpt\Leftrightarrow-3\le x< 2\)
d) \(\dfrac{2x-5}{3x+2}< \dfrac{3x+2}{2x-5}\)
\(\Leftrightarrow\dfrac{2x-5}{3x+2}-\dfrac{3x+2}{2x-5}< 0\)
\(\Leftrightarrow\dfrac{\left(2x-5\right)^2-\left(3x+2\right)^2}{\left(3x+2\right)\left(2x-5\right)}< 0\)
\(\Leftrightarrow\dfrac{\left(2x-5+3x+2\right)\left(2x-5-3x-2\right)}{\left(3x+2\right)\left(2x-5\right)}< 0\)
\(\Leftrightarrow\dfrac{-\left(5x-3\right)\left(x+7\right)}{\left(3x+2\right)\left(2x-5\right)}< 0\)
Lập bảng xét dấu ta được kết quả :
\(Bpt\Leftrightarrow\left[{}\begin{matrix}-7< x< -\dfrac{2}{3}\\\dfrac{5}{3}< x< \dfrac{5}{2}\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Giải các bất phương trình saua/ (x+1).(x-1).(3x-6)0b/ dfrac{x+3}{x-2}le0c/ dfrac{left(2x-5right).left(x+2right)}{-4x+3}ge0d/ dfrac{2x-5}{3x+2} dfrac{3x+2}{2x-5}e/ dfrac{2x^2+x}{1-2x}ge1-xf/ dfrac{left(2+xright)^5.left(x+1right).left(3-xright)^{11}}{left(2-xright).left(1-xright)^{20}}le0
Đọc tiếp
Giải các bất phương trình sau
a/ (x+1).(x-1).(3x-6)>0
b/ \(\dfrac{x+3}{x-2}\le0\)
c/ \(\dfrac{\left(2x-5\right).\left(x+2\right)}{-4x+3}\ge0\)
d/ \(\dfrac{2x-5}{3x+2}< \dfrac{3x+2}{2x-5}\)
e/ \(\dfrac{2x^2+x}{1-2x}\ge1-x\)
f/ \(\dfrac{\left(2+x\right)^5.\left(x+1\right).\left(3-x\right)^{11}}{\left(2-x\right).\left(1-x\right)^{20}}\le0\)
Bài 3 : Xét dấu biểu thức sau :
1 , fleft(xright)frac{x-7}{4x^2-19x+12}
2 , fleft(xright)frac{11x+3}{-x^2+5x-7}
3 , fleft(xright)frac{3x-2}{x^3-3x^2+2}
4 , fleft(xright)frac{x^2+4x-12}{sqrt{6}x^2+3x+sqrt{2}}
5 , fleft(xright)frac{x^2-3x-2}{-x^2+x-1}
6 , fleft(xright)frac{x^3-5x+4}{x^4-4x^3+8x-5}
7 , fleft(xright)frac{left(x+3right)left(x-2right)left(-2x^2+x-1right)}{left(2x-5right)left(x^2+3x-10right)}
8 , fleft(xright)left(-x^2+x-1right)left(6x^2-5x+1right)
9 , fleft(xright)frac{x^2-...
Đọc tiếp
Bài 3 : Xét dấu biểu thức sau :
1 , \(f\left(x\right)=\frac{x-7}{4x^2-19x+12}\)
2 , \(f\left(x\right)=\frac{11x+3}{-x^2+5x-7}\)
3 , \(f\left(x\right)=\frac{3x-2}{x^3-3x^2+2}\)
4 , \(f\left(x\right)=\frac{x^2+4x-12}{\sqrt{6}x^2+3x+\sqrt{2}}\)
5 , \(f\left(x\right)=\frac{x^2-3x-2}{-x^2+x-1}\)
6 , \(f\left(x\right)=\frac{x^3-5x+4}{x^4-4x^3+8x-5}\)
7 , \(f\left(x\right)=\frac{\left(x+3\right)\left(x-2\right)\left(-2x^2+x-1\right)}{\left(2x-5\right)\left(x^2+3x-10\right)}\)
8 , \(f\left(x\right)=\left(-x^2+x-1\right)\left(6x^2-5x+1\right)\)
9 , \(f\left(x\right)=\frac{x^2-x-2}{-x^2+3x+4}\)
10 , \(f\left(x\right)=\left(x^2-5x+4\right)\left(2-5x+2x^2\right)\)
1.
\(f\left(x\right)=\frac{x-7}{\left(x-4\right)\left(4x-3\right)}\)
Vậy:
\(f\left(x\right)\) ko xác định tại \(x=\left\{\frac{3}{4};4\right\}\)
\(f\left(x\right)=0\Rightarrow x=7\)
\(f\left(x\right)>0\Rightarrow\left[{}\begin{matrix}\frac{3}{4}< x< 4\\x>7\end{matrix}\right.\)
\(f\left(x\right)< 0\Rightarrow\left[{}\begin{matrix}x< \frac{3}{4}\\4< x< 7\end{matrix}\right.\)
2.
\(f\left(x\right)=\frac{11x+3}{-\left(x-\frac{5}{2}\right)^2-\frac{3}{4}}\)
Vậy:
\(f\left(x\right)=0\Rightarrow x=-\frac{3}{11}\)
\(f\left(x\right)>0\Rightarrow x< -\frac{3}{11}\)
\(f\left(x\right)< 0\Rightarrow x>-\frac{3}{11}\)
3.
\(f\left(x\right)=\frac{3x-2}{\left(x-1\right)\left(x^2-2x-2\right)}\)
Vậy:
\(f\left(x\right)\) ko xác định khi \(x=\left\{1;1\pm\sqrt{3}\right\}\)
\(f\left(x\right)=0\Rightarrow x=\frac{2}{3}\)
\(f\left(x\right)>0\Rightarrow\left[{}\begin{matrix}x< 1-\sqrt{3}\\\frac{2}{3}< x< 1\\x>1+\sqrt{3}\end{matrix}\right.\)
\(f\left(x\right)< 0\Rightarrow\left[{}\begin{matrix}1-\sqrt{3}< x< \frac{2}{3}\\1< x< 1+\sqrt{3}\end{matrix}\right.\)
4.
\(f\left(x\right)=\frac{\left(x-2\right)\left(x+6\right)}{\sqrt{6}\left(x+\frac{\sqrt{6}}{4}\right)^2+\frac{8\sqrt{2}-3\sqrt{6}}{8}}\)
Vậy:
\(f\left(x\right)=0\Rightarrow x=\left\{-6;2\right\}\)
\(f\left(x\right)>0\Rightarrow\left[{}\begin{matrix}x< -6\\x>2\end{matrix}\right.\)
\(f\left(x\right)< 0\Rightarrow-6< x< 2\)
5.
\(f\left(x\right)=\frac{x^2-3x-2}{-\left(x-\frac{1}{2}\right)^2-\frac{3}{4}}\)
Vậy:
\(f\left(x\right)=0\Rightarrow x=\frac{3\pm\sqrt{17}}{2}\)
\(f\left(x\right)>0\Rightarrow\frac{3-\sqrt{17}}{2}< x< \frac{3+\sqrt{17}}{2}\)
\(f\left(x\right)< 0\Rightarrow\left[{}\begin{matrix}x< \frac{3-\sqrt{17}}{2}\\x>\frac{3+\sqrt{17}}{2}\end{matrix}\right.\)
6.
\(f\left(x\right)=\frac{\left(x-1\right)\left(x^2+x-4\right)}{\left(x-1\right)^2\left(x^2-2x-5\right)}=\frac{x^2+x-4}{\left(x-1\right)\left(x^2-2x-5\right)}\)
Vậy:
\(f\left(x\right)\) ko xác định khi \(x=\left\{1;1\pm\sqrt{6}\right\}\)
\(f\left(x\right)=0\Rightarrow x=\left\{\frac{-1\pm\sqrt{17}}{2}\right\}\)
\(f\left(x\right)>0\Rightarrow\left[{}\begin{matrix}\frac{-1-\sqrt{17}}{2}< x< 1-\sqrt{6}\\1< x< \frac{-1+\sqrt{17}}{2}\\x>1+\sqrt{6}\end{matrix}\right.\)
\(f\left(x\right)< 0\Rightarrow\left[{}\begin{matrix}x< \frac{-1-\sqrt{17}}{2}\\1-\sqrt{6}< x< 1\\\frac{-1+\sqrt{17}}{2}< x< 1+\sqrt{6}\end{matrix}\right.\)
Xem thêm câu trả lời