Giải và biện luận pT tham số m
mx2-(m+1)x+2>=0
Giải và biện luận theo tham số m các phương trình sau
m x 2 + ( 2 m - 1 ) x + m - 2 = 0
m = 0 phương trình trở thành
-x - 2 = 0 ⇒ x = -2
m ≠ 0 phương trình đã cho là phương trình bậc hai, có Δ = 4m + 1
Với m < -1/4 phương trình vô nghiệm;
Với m ≥ -1/4 nghiệm của phương trình là
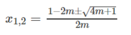
Giair và biện luận các bất PT sau theo tham số m:
1) x + 3m > 3 + mx
2) \(25m^2-2x< m^2x-25\)
3) \(3x-m^2\ge mx-4m+3\)
4) \(m\left(x-m\right)\ge3x-9\)
1. \(x+3m>3+mx.\Leftrightarrow x+3m-3-mx>0.\\ \Leftrightarrow\left(1-m\right)x+3m-3>0.\\ \Leftrightarrow\left(1-m\right)x>-3m+3.\left(1\right)\)
+) Nếu \(1-m=0.\Leftrightarrow m=1.\) Thay vào (1):
\(0x>-3.1+3.\Leftrightarrow0x>0\) (vô lý).
\(\Rightarrow\) Bất phương trình vô nghiệm.
+) Nếu \(1-m>0.\Leftrightarrow m< 1.\)
Khi đó (1) có nghiệm: \(x>\dfrac{-3m+3}{1-m}.\Leftrightarrow x>\dfrac{-3\left(m-1\right)}{-\left(m-1\right)}.\Leftrightarrow x>3.\)
+) Nếu \(1-m< 0.\Leftrightarrow m>1.\)
Khi đó (1) có nghiệm: \(x< \dfrac{-3m+3}{1-m}.\Leftrightarrow x< 3.\)
1/ x=3 , m=1
bl : tìm nghiệm , tạo khoảng thử nghiệm
2/ \(m=\pm\sqrt{-\dfrac{25-2x}{25-x}}\)
\(x=\dfrac{25\left(1+m^2\right)}{2+m^2}\)
3/ x=-m+1
m = \(\left\{{}\begin{matrix}3\\-x+1\end{matrix}\right.\)
4/ m= \(\left\{{}\begin{matrix}x-3\\3\end{matrix}\right.\)
x= m+3
giải và biện luận pt chứa tham số m a) m(x-1)=5-(m-1)x b) m(mx-1)=x+1
a) Ta có: \(m\left(x-1\right)=5-\left(m-1\right)x\)
\(\Leftrightarrow mx-m-5+mx-x=0\)
\(\Leftrightarrow\left(2m-1\right)x=5\)
-Nếu \(2m-1\ne0\Leftrightarrow m\ne\dfrac{1}{2}\) :pt có dạng \(x=\dfrac{5}{2m-1}\)
=>pt có nghiệm \(x=\dfrac{5}{2m-1}\)
-Nếu \(2mm-1=0\Leftrightarrow m=\dfrac{1}{2}\):pt có dạng \(0x=5\)
\(\Rightarrow\) PT vô nghiệm
Kết luận: Nếu \(m\ne\dfrac{1}{2}\) thì pt có nghiệm \(x=\dfrac{5}{2m-1}\)
Nếu \(m=\dfrac{1}{2}\) thì pt vô nghiệm
d) Ta có: \(m\left(mx-1\right)=x+1\)
\(\Leftrightarrow\left(m^2-1\right)x=m+1\)
\(\Leftrightarrow\left(m-1\right)\left(m+1\right)x=m+1\)
-Nếu\(m=1\) : pt \(\Leftrightarrow0x=2\): pt vô nghiệm
-Nếu\(m\ne1\): pt\(\Leftrightarrow x=\dfrac{1}{m-1}\)
+nếu \(m=-1\): pt \(0x=0\) : pt có vô số nghiệm \(x\) thuộc R
+ nếu \(m\ne-1\): pt \(\Leftrightarrow x=\dfrac{1}{m-1}\)
Kết luận: Nếu \(m=1\) thì pt vô nghiệm
Nếu \(m\ne1\) ,\(m\ne1\) thì pt có nghiệm \(x=\dfrac{1}{m-1}\)
Nếu \(m=-1\) thì pt có vô số nghiệm \(x\) thuộc R
a: =>mx-m=5-mx+x
=>mx-m-5+mx-x=0
=>x(m+m-1)=m+5
=>x(2m-1)=m+5
Để phương trình vô nghiệm thì 2m-1=0
=>m=1/2
Để phương trình có nghiệm duy nhất thì 2m-1<>0
=>m<>1/2
b: =>m^2x-m-x-1=0
=>x(m^2-1)=m+1
Để phương trình có vô số nghiệm thì m+1=0
=>m=-1
Để phương trìnhvô nghiệm thì m-1=0
=>m=1
Để phương trình có nghiệm duy nhất thì m^2-1<>0
=>m<>1 và m<>-1
câu 2 cho pt bậc hai ẩn x(m là tham số ):\(x^2+2\left(m-1\right)x-2m+5=0\)
1)giải và biện luận số nghiệm của\(x_1;x_2\) của (m) theo tham số m
2)tìm m sao cho \(x_{1;}x_2\) thoả mãn:
a)\(\dfrac{x_1}{x_2}+\dfrac{x_2}{x_1}=2\)
b)\(x_1+x_2+2x_1x_2\le6\)
a, \(\Delta'=\left(m-1\right)^2-\left(-2m+5\right)=m^2-2m+1+2m-5=m^2-4\)
Để pt vô nghiệm thì \(m^2-4< 0\Leftrightarrow-2< m< 2\)
Để pt có nghiệm kép thì \(m^2-4=0\Leftrightarrow m=\pm2\)
Để pt có 2 nghiệm phân biệt thì \(m^2-4>0\Leftrightarrow\left[{}\begin{matrix}m< -2\\m>2\end{matrix}\right.\)
2, Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=2m-2\\x_1x_2=-2m+5\end{matrix}\right.\)
\(a,ĐKXĐ:x_1,x_2\ne0\\ \dfrac{x_1}{x_2}+\dfrac{x_2}{x_1}=2\\ \Leftrightarrow\dfrac{x_1^2+x_2^2}{x_1x_2}=2\\ \Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=0\\ \Leftrightarrow\left(2m-2\right)^2-4\left(-2m+5\right)=0\\ \Leftrightarrow4m^2-8m+4+8m-20=0\\ \Leftrightarrow4m^2-16=0\\ \Leftrightarrow m=\pm2\)
\(b,x_1+x_2+2x_1x_2\le6\\ \Leftrightarrow2m-2+2\left(-2m+5\right)\le6\\ \Leftrightarrow2m-2-4m+10-6\le0\\ \Leftrightarrow-2m+2\le0\\ \Leftrightarrow m\ge1\)
1. Cho f(x) và g(x) có đạo hàm trên R. Tính đạo hàm của
a, y=f(x3)-g(x2)
b, y=\(\sqrt{f^3\left(x\right)+g^3\left(x\right)}\)
2. Cho f(x)=\(\dfrac{m-1}{4}\)x4 + \(\dfrac{m-2}{3}\)x3-mx2+3x-1. Giải và biện luận pt: f'(x)=0
1a.
\(y'=3x^2.f'\left(x^3\right)-2x.g'\left(x^2\right)\)
b.
\(y'=\dfrac{3f^2\left(x\right).f'\left(x\right)+3g^2\left(x\right).g'\left(x\right)}{2\sqrt{f^3\left(x\right)+g^3\left(x\right)}}\)
2.
\(f'\left(x\right)=\left(m-1\right)x^3+\left(m-2\right)x^2-2mx+3=0\)
Để ý rằng tổng hệ số của vế trái bằng 1 nên pt luôn có nghiệm \(x=1\), sử dụng lược đồ Hooc-ne ta phân tích được:
\(\Leftrightarrow\left(x-1\right)\left[\left(m-1\right)x^2+\left(2m-3\right)x-3\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\\left(m-1\right)x^2+\left(2m-3\right)x-3=0\left(1\right)\end{matrix}\right.\)
Xét (1), với \(m=1\Rightarrow x=-3\)
- Với \(m\ne1\Rightarrow\Delta=\left(2m-3\right)^2+12\left(m-1\right)=4m^2-3\)
Nếu \(\left|m\right|< \dfrac{\sqrt{3}}{2}\Rightarrow\) (1) vô nghiệm \(\Rightarrow f'\left(x\right)=0\) có đúng 1 nghiệm
Nếu \(\left|m\right|>\dfrac{\sqrt{3}}{2}\Rightarrow\left(1\right)\) có 2 nghiệm \(\Rightarrow f'\left(x\right)=0\) có 3 nghiệm
Giải và biện luận theo tham số m pt: m2 (x - 1) -2mx-9= m(x-6)
giải và biện luận pt : \(\left(m^2+2\right)x=x-2m\) ( m là tham số )
phương trình \(\Leftrightarrow\) \(\left(m^2+1\right)x=-2m\) \(\Leftrightarrow\) \(x=-\frac{2m}{m^2+1}\)
đây là nghiệm duy nhất cần tìm
giải và biện luận pt:
\(\left(m^2-1\right)x^2-2\left(m-1\right)x+1=0\)
Với \(m=-1\Leftrightarrow4x+1=0\Leftrightarrow x=-\dfrac{1}{4}\)
Với \(m=1\Leftrightarrow1=0\Leftrightarrow x\in\varnothing\)
Với \(m\ne\pm1\)
\(\Delta=4\left(m-1\right)^2-4\left(m^2+1\right)\\ \Delta=4m^2-8m+4-4m^2-4\\ \Delta=-8m\)
PT vô nghiệm \(\Leftrightarrow-8m< 0\Leftrightarrow m>0\)
PT có nghiệm kép \(\Leftrightarrow-8m=0\Leftrightarrow m=0\)
Khi đó \(x=\dfrac{2\left(m-1\right)}{2\left(m^2-1\right)}=\dfrac{1}{m+1}\)
PT có 2 nghiệm phân biệt \(\Leftrightarrow-8m>0\Leftrightarrow m< 0\)
Khi đó \(\left[{}\begin{matrix}x_1=\dfrac{2\left(m-1\right)-\sqrt{-8m}}{2\left(m^2-1\right)}\\x_2=\dfrac{2\left(m-1\right)+\sqrt{-8m}}{2\left(m^2+1\right)}\end{matrix}\right.\)
Giải và biện luận tham số nghiệm Pt theo tham số m:
a, \(\text{(m - 3)x - 4 = 0}\)
b, \(\text{(m^2 + 1)x + 2 + = 0}\)
c, \(\left(m^2-4\right)x-3=0\)
d, \(\left(m^2-9\right)x+3=m\)