§3. Dấu của nhị thức bậc nhất

a. 

Khi \(m=2\) BPT tương đương:

\(x^2+6>0\) (luôn đúng)

Vậy nghiệm của BPT là \(x\in R\)

b.

(1) nghiệm đúng với mọi x khi và chỉ khi:

\(\Delta'=\left(m-2\right)^2-\left(m+4\right)< 0\)

\(\Leftrightarrow m^2-5m< 0\)

\(\Rightarrow0< m< 5\)

\(f\left(x\right)=x.x.\left(3-2x\right)\le\left(\dfrac{x+x+3-2x}{3}\right)^3=1\)

\(f\left(x\right)_{max}=1\)

D.1

B

D là đáp án đúng (do tập xác định của BPT bằng rỗng)

B

\(\dfrac{1}{1-x}\ge2=>2\left(1-x\right)\le1\\ =>2-2x\le1\\ =>2x\le1\\ =>x\le\dfrac{1}{2}\)

\(\dfrac{1}{1-x}-2\ge0\Leftrightarrow\dfrac{1-2+2x}{1-x}\ge0\Leftrightarrow\dfrac{2x-1}{x-1}\le0\)

TH1 : \(\left\{{}\begin{matrix}2x-1< 0\\x-1>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< \dfrac{1}{2}\\x>1\end{matrix}\right.\)( vô lí ) 

TH2 : \(\left\{{}\begin{matrix}2x-1>0\\x-1< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>\dfrac{1}{2}\\x< 1\end{matrix}\right.\Leftrightarrow\dfrac{1}{2}< x< 1\)

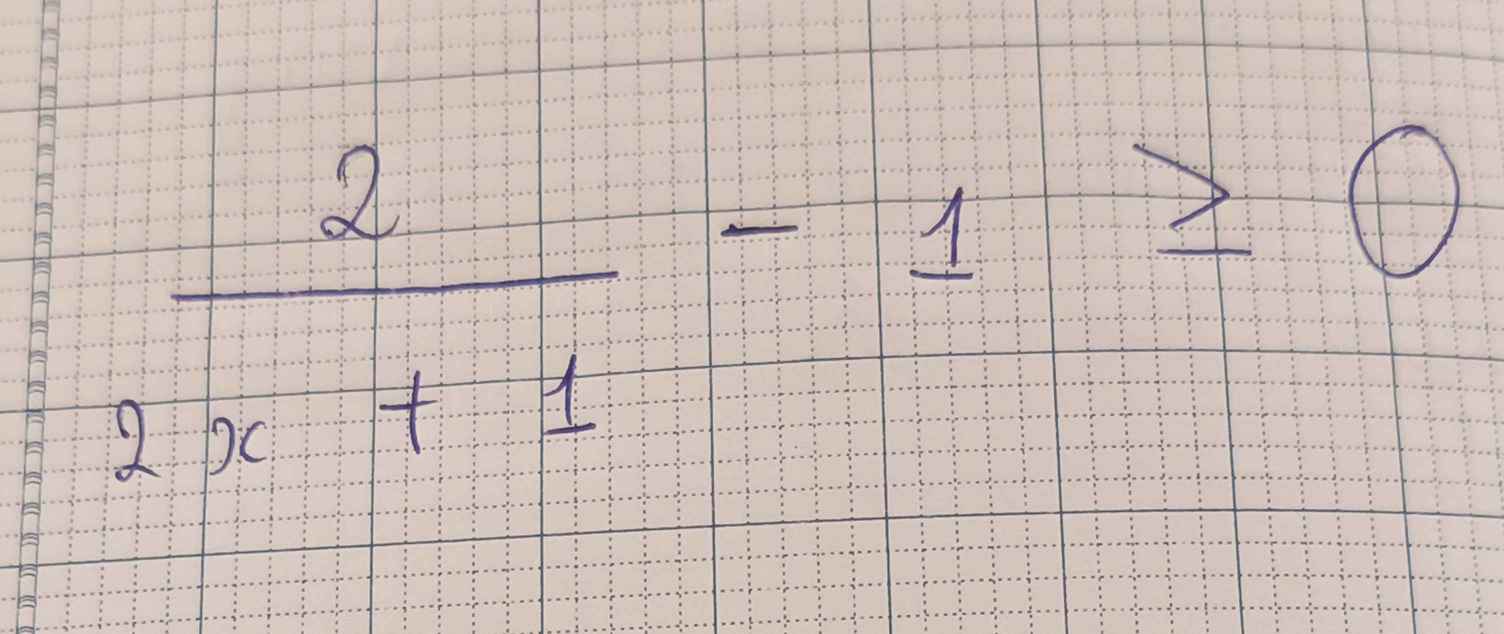
\(\dfrac{2}{2x+1}-1\ge0\Leftrightarrow\dfrac{2}{2x+1}-\dfrac{2x+1}{2x+1}\ge0\)

\(\Leftrightarrow\dfrac{2-\left(2x+1\right)}{2x+1}\ge0\)

\(\Leftrightarrow\dfrac{1-2x}{2x+1}\ge0\)

\(\Rightarrow-\dfrac{1}{2}< x\le\dfrac{1}{2}\)

\(a)\left(x-2\right)\left(x^2+2x-3\right)\ge0.\)

Đặt \(f\left(x\right)=\left(x-2\right)\left(x^2+2x-3\right).\)

Ta có: \(x-2=0.\Leftrightarrow x=2.\\ x^2+2x-3=0.\Leftrightarrow\left[{}\begin{matrix}x=1.\\x=-3.\end{matrix}\right.\)

Bảng xét dấu:

x                   \(-\infty\)       -3       1       2     \(+\infty\)

\(x-2\)                    -      |    -   |   -   0   +

\(x^2+2x-3\)         +     0    -   0  +   |    +

\(f\left(x\right)\)                     -     0    +  0   -  0   +

Vậy \(f\left(x\right)\ge0.\Leftrightarrow x\in\left[-3;1\right]\cup[2;+\infty).\)

\(b)\dfrac{x^2-9}{-x+5}< 0.\)

Đặt \(g\left(x\right)=\dfrac{x^2-9}{-x+5}.\)

Ta có: \(x^2-9=0.\Leftrightarrow\left[{}\begin{matrix}x=3.\\x=-3.\end{matrix}\right.\)

\(-x+5=0.\Leftrightarrow x=5.\)

Bảng xét dấu:

x            \(-\infty\)      -3       3        5       \(+\infty\)

\(x^2-9\)            +   0   -   0   +   |    +

\(-x+5\)          +    |   +   |    +  0    -

\(g\left(x\right)\)              +    0   -   0   +  ||    -

Vậy \(g\left(x\right)< 0.\Leftrightarrow x\in\left(-3;3\right)\cup\left(5;+\infty\right).\)