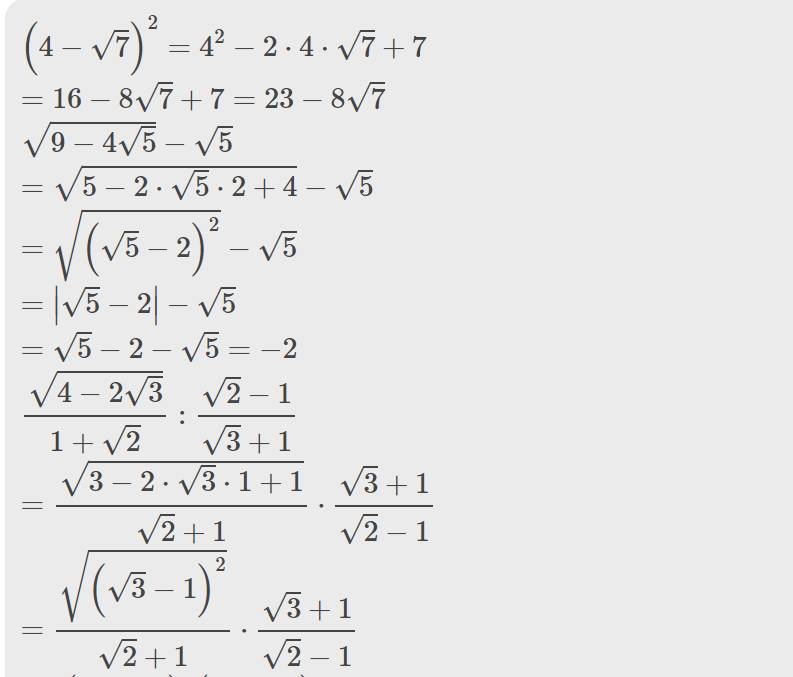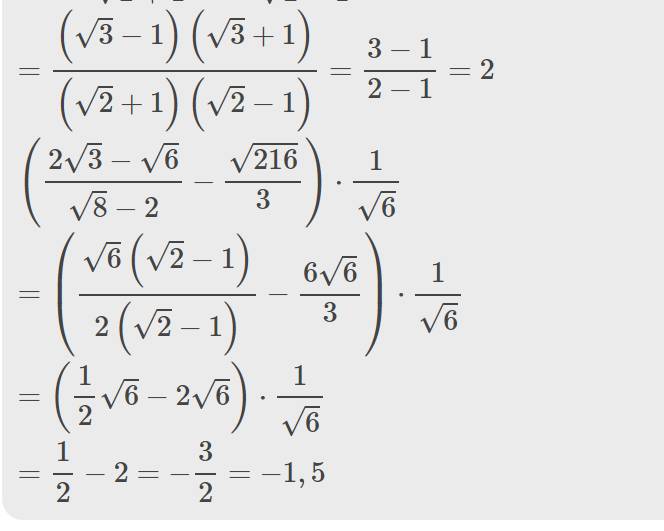Chứng minh (4–√7)²=23–8√7
NA
Những câu hỏi liên quan
Chứng minh rằng : 23-8√7=(4-√7) 2 2 là mũ hai
\(\left(4-\sqrt{7}\right)^2=4^2-2\cdot4\cdot\sqrt{7}+7=23-8\sqrt{7}\)
Đúng 0
Bình luận (0)
Chứng minh đẳng thức:
\(\sqrt{9-4\sqrt{5}}-\sqrt{5}=-2\)
\(\sqrt{23+8\sqrt{7}}-\sqrt{7=4}\)
\(\sqrt{\sqrt{5}^2-2.2\sqrt{5}+4}-\sqrt{5}=\sqrt{\left(\sqrt{5}-2\right)^2}-\sqrt{5}=\sqrt{5}-2-\sqrt{5}=-2\left(dpcm\right)\)\(\sqrt{23+8\sqrt{7}}-\sqrt{7}=\sqrt{\sqrt{7}^2+2.4\sqrt{7}+16}-\sqrt{7}\)\(=\sqrt{\left(\sqrt{7}+4\right)^2}-\sqrt{7}=\sqrt{7}+4-\sqrt{7}=4\left(DPCM\right)\)
Đúng 0
Bình luận (0)
Chứng minh :
a) \(9+4\sqrt{5}=\left(\sqrt{5}+2\right)^2\)
b) \(\sqrt{9-4\sqrt{5}}-\sqrt{5}=-2\)
c) \(\left(4-\sqrt{7}\right)^2=23-8\sqrt{7}\)
d) \(\sqrt{23+8\sqrt{7}}-\sqrt{7}=4\)
a) \(9+4\sqrt{5}=4+4\sqrt{5}+5=2^2+2\cdot2\sqrt{5}+\left(\sqrt{5}\right)^2=\left(\sqrt{5}+2\right)^2\left(ĐPCM\right)\)
Đúng 0
Bình luận (0)
a) \(9+4\sqrt{5}=\left(\sqrt{5}\right)^2+2.\sqrt{5}.2+2^2=\left(\sqrt{5}+2\right)^2\left(đpcm\right)\)
b)\(\sqrt{9-4\sqrt{5}}-\sqrt{5}=\sqrt{\left(\sqrt{5}-2\right)^2}-\sqrt{5}=\sqrt{5}-2-\sqrt{5}=-2\left(đpcm\right)\)
c)\(\left(4-\sqrt{7}\right)^2=16-8\sqrt{7}+7=23-8\sqrt{7}\left(đpcm\right)\)
d)\(\sqrt{23+8\sqrt{7}}-\sqrt{7}=\sqrt{\left(4+\sqrt{7}\right)^2}-\sqrt{7}=4+\sqrt{7}-\sqrt{7}=4\left(đpcm\right)\)
Đúng 0
Bình luận (0)
chứng minh
\(9+4\sqrt{5}=\left(\sqrt{5}+2\right)^2\)
\(\sqrt{23+8\sqrt{7}}-\sqrt{7}=4\)
Chứng minh: 23 + 8 7 - 7 = 4
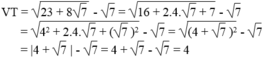
Vế trái bằng vế phải nên đẳng thức được chứng minh.
Đúng 0
Bình luận (0)
Chứng minh đẳng thức
\(\left(4-\sqrt{7}\right)^2=23-8\sqrt{7}\)
\(\sqrt{9-4\sqrt{5}}-\sqrt{5}=-2\)
\(\dfrac{\sqrt{4-2\sqrt{3}}}{1+\sqrt{2}}:\dfrac{\sqrt{2}-1}{\sqrt{3}+1}=2\)
\(\left(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\dfrac{\sqrt{216}}{3}\right).\dfrac{1}{\sqrt{6}}=-1,5\)
\(\left(4-\sqrt{7}\right)^2=4^2-2\cdot4\cdot\sqrt{7}+7\)
\(=16-8\sqrt{7}+7=23-8\sqrt{7}\)
\(\sqrt{9-4\sqrt{5}}-\sqrt{5}\)
\(=\sqrt{5-2\cdot\sqrt{5}\cdot2+4}-\sqrt{5}\)
\(=\sqrt{\left(\sqrt{5}-2\right)^2}-\sqrt{5}\)
\(=\left|\sqrt{5}-2\right|-\sqrt{5}\)
\(=\sqrt{5}-2-\sqrt{5}=-2\)
\(\dfrac{\sqrt{4-2\sqrt{3}}}{1+\sqrt{2}}:\dfrac{\sqrt{2}-1}{\sqrt{3}+1}\)
\(=\dfrac{\sqrt{3-2\cdot\sqrt{3}\cdot1+1}}{\sqrt{2}+1}\cdot\dfrac{\sqrt{3}+1}{\sqrt{2}-1}\)
\(=\dfrac{\sqrt{\left(\sqrt{3}-1\right)^2}}{\sqrt{2}+1}\cdot\dfrac{\sqrt{3}+1}{\sqrt{2}-1}\)
\(=\dfrac{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}{\left(\sqrt{2}+1\right)\left(\sqrt{2}-1\right)}=\dfrac{3-1}{2-1}=2\)
\(\left(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\dfrac{\sqrt{216}}{3}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\left(\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}-\dfrac{6\sqrt{6}}{3}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\left(\dfrac{1}{2}\sqrt{6}-2\sqrt{6}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\dfrac{1}{2}-2=-\dfrac{3}{2}=-1,5\)
Đúng 1
Bình luận (0)
Chứng minh đẳng thức
\(\left(4-\sqrt{7}\right)^2=23-8\sqrt{7}\)
\(\sqrt{9-4\sqrt{5}}-\sqrt{5}=-2\)
\(\dfrac{\sqrt{4-2\sqrt{3}}}{1+\sqrt{2}}:\dfrac{\sqrt{2}-1}{\sqrt{3}-1}=2\)
\(\left(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\dfrac{\sqrt{216}}{3}\right).\dfrac{1}{\sqrt{6}}=-1,5\)
Chứng minh:
a. 9+4\(\sqrt{5}\)= (\(\sqrt{5}\)+2)2
b. \(\sqrt{23+8\sqrt{ }7}\) - \(\sqrt{7}\) = 4
a. 9+4\(\sqrt{5}\)=(\(\sqrt{5}\)+2)2
VT: 9+4\(\sqrt{5}\)=2\(^2\)+2.2.\(\sqrt{5}\)+(\(\sqrt{5}\))\(^2\)=(2+\(\sqrt{5}\))\(^2\)=VP
b. \(\sqrt{23+8\sqrt{7}}\)-\(\sqrt{7}\)=4
\(\Leftrightarrow\)\(\sqrt{4^2+2.4\sqrt{7}+\left(\sqrt{7}\right)^2}\)-\(\sqrt{7}\)=4
\(\Leftrightarrow\)\(\sqrt{4+\sqrt{7}}^2\)-\(\sqrt{7}\)=4
\(\Leftrightarrow\)4+\(\sqrt{7}\)-\(\sqrt{7}\)=4
\(\Leftrightarrow\)4=4
\(\Rightarrow\)VT=VP
\(\sqrt{5}\)\(\sqrt{5}\)
Đúng 0
Bình luận (1)
Chứng minh rang
E = 1+7^4+7^8+7^12 +...+7^36 . chứng minh E chia het cho 35
Ta có \(7^4\) chia hết cho 7; \(7^8\) chia hết cho 7; ... \(7^{36}\) chia hết cho 7
\(\Rightarrow7^4+7^8+...+7^{36}\) chia hết cho 7
Mà 1 không chia hết cho 7
\(\Rightarrow E=1+7^4+7^8+...+7^{36}\) không chia hết cho 7
Mà 35 chia hết cho 7
\(\Rightarrow E\) không chia hết cho 35
\(\Rightarrow\) Đề sai for sure!
Đúng 0
Bình luận (0)