log5 = a. Tính log\(\dfrac{1}{64}\) theo a
HD
Những câu hỏi liên quan
Cho log5 a. Tính log 25000 theo a A.
5
a
B.
5
a
2
C.
2
a
2
+
1
D.
2
a
+
3
Đọc tiếp
Cho log5 = a. Tính log 25000 theo a
A. 5 a
B. 5 a 2
C. 2 a 2 + 1
D. 2 a + 3
Đáp án D
Ta có log25000 = log25 + log1002log5 + 3 = 2a + 3
Đúng 0
Bình luận (0)
1. cho a=log3 2 và b=log3 5. tính các logarit sau theo a, b; A=log3 80, B=log3 37,5
2. cho log10 3=a, log5=b. tính C=log30 8 theo a, b
3. cho log27 5=a, log8 7=b, log2 3=c. tính D log6 35 theo a, b, c
Bài 1:
\(A=\log_380=\log_3(2^4.5)=\log_3(2^4)+\log_3(5)\)
\(=4\log_32+\log_35=4a+b\)
\(B=\log_3(37,5)=\log_3(2^{-1}.75)=\log_3(2^{-1}.3.5^2)\)
\(=\log_3(2^{-1})+\log_33+\log_3(5^2)=-\log_32+1+2\log_35\)
\(=-a+1+2b\)
Đúng 0
Bình luận (0)
Bài 2:
\(\log_{30}8=\frac{\log 8}{\log 30}=\frac{\log (2^3)}{\log (10.3)}=\frac{3\log2}{\log 10+\log 3}\)
\(=\frac{3\log (\frac{10}{5})}{1+\log 3}=\frac{3(\log 10-\log 5)}{1+\log 3}=\frac{3(1-b)}{1+a}\)
Đúng 0
Bình luận (0)
Bài 3:
\(\log_{27}5=a; \log_87=b; \log_23=c\)
\(\Leftrightarrow \frac{\ln 5}{\ln 27}=a; \frac{\ln 7}{\ln 8}=b; \frac{\ln 3}{\ln 2}=c\)
\(\Leftrightarrow \frac{\ln 5}{\ln (3^3)}=a; \frac{\ln 7}{\ln (2^3)}=b; \ln 3=c\ln 2\)
\(\Leftrightarrow \frac{\ln 5}{3\ln 3}=a; \frac{\ln 7}{3\ln 2}=b; \ln 3=c\ln 2\)
\(\Rightarrow \frac{\ln 5}{3c\ln 2}=a; \frac{\ln 7}{3\ln 2}=b\)
\(\Rightarrow \ln 35=\ln 5+\ln 7=3ac\ln 2+3b\ln 2\)
Do đó:
\(D=\log_6 35=\frac{\ln 35}{\ln 6}=\frac{\ln 35}{\ln 2+\ln 3}=\frac{\ln 35}{\ln 2+c\ln 2}=\frac{3ac\ln 2+3b\ln 2}{\ln 2+c\ln 2}\)
\(=\frac{3ac+3b}{1+c}\)
Đúng 0
Bình luận (0)
Tính :
a) \(\left(\dfrac{1}{9}\right)^{\dfrac{1}{2}\log^4_3}\)
b) \(10^{3-\log5}\)
c) \(2\log_{27}\log1000\)
d) \(3\log_2\log_416+\log_{\dfrac{1}{2}}2\)
a) \(\left(\dfrac{1}{9}\right)^{\dfrac{1}{2}log^4_3}=\left(3^{-2}\right)^{\dfrac{1}{2}log^4_3}=\left(3^{log^4_3}\right)^{-2.\dfrac{1}{2}}=4^{-1}=\dfrac{1}{4}\);
b) \(10^{3-log5}=\dfrac{10^3}{10^{log5}}=\dfrac{10^3}{5}=200\);
c) \(2log^{log1000}_{27}=2log^3_{3^3}=\dfrac{2}{3}log^3_3=\dfrac{2}{3}\);
d) \(3log_2^{log_4^{16}}+log^2_{\dfrac{1}{2}}=3log^2_2-log^2_2=3-1=2\).
Đúng 0
Bình luận (0)
Cho
log
5
a
. Tính
log
25000
theo a. A. 5a B.
5
a
2
C.
2
a
2
+
1
D.
2
a
+
3
Đọc tiếp
Cho log 5 = a . Tính log 25000 theo a.
A. 5a
B. 5 a 2
C. 2 a 2 + 1
D. 2 a + 3
Biết phương trình log5\(\dfrac{2\sqrt{x}+1}{x}\) = 2.log3\(\left(\dfrac{\sqrt{x}}{2}-\dfrac{1}{2\sqrt{x}}\right)\) có một nghiệm dạng x= a + b\(\sqrt{2}\) trong đó a,b là các số nguyên. Tính 2a+b
Bài này e rằng quá khó để tự luận do vấn đề cơ số
Nhưng tinh ý 1 chút thì giải trắc nghiệm đơn giản:
\(\dfrac{\sqrt{x}}{2}-\dfrac{1}{2\sqrt{x}}=\dfrac{x-1}{2\sqrt{x}}\)
Để ý rằng \(x-1-2\sqrt{x}=x-\left(2\sqrt{x}+1\right)\)
Do đó pt luôn có nghiệm thỏa mãn: \(x-2\sqrt{x}-1=0\Rightarrow x=3+2\sqrt{2}\)
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của tham số m để bất phương trình \(\log5+\log\left(x^2+1\right)\ge\log\left(mx^2+4x+m\right)\) đúng với mọi \(x\)?
A. 0
B. 1
C. 2
D. 4
\(log\left(5\left(x^2+1\right)\right)\ge log\left(mx^2+4x+m\right)\)
- BPT đúng \(\forall x\Rightarrow log\left(mx^2+4x+m\right)\) xác định \(\forall x\in R\)
\(\Rightarrow mx^2+4x+m>0\) \(\forall x\in R\)
\(\Rightarrow\left\{{}\begin{matrix}a=m>0\\\Delta'=4-m^2< 0\end{matrix}\right.\) \(\Rightarrow m>2\) (1)
- Lại có \(x^2+1\ge1\) \(\forall x\)
\(\Rightarrow5\left(x^2+1\right)\ge mx^2+4x+m\)
\(\Leftrightarrow5\left(x^2+1\right)-4x\ge m\left(x^2+1\right)\)
\(\Leftrightarrow5-\dfrac{4x}{x^2+1}\ge m\)
Đặt \(f\left(x\right)=5-\dfrac{4x}{x^2+1}\Rightarrow f\left(x\right)\ge m\) \(\forall x\Leftrightarrow m\le min\left(f\left(x\right)\right)\)
Ta có \(f\left(x\right)=3+2-\dfrac{4x}{x^2+1}=3+\dfrac{2\left(x-1\right)^2}{x^2+1}\ge3\)
\(\Rightarrow min\left(f\left(x\right)\right)=3\Rightarrow m\le3\) (2)
Kết hợp (1), (2) \(\Rightarrow2< m\le3\Rightarrow m=3\)
Vậy có 1 giá trị nguyên duy nhất của m để BPT đúng với mọi x
Đáp án B
Đúng 0
Bình luận (0)
Đặt a log2 3; b log5 6. Tính T log15 6 theo a, b.
Đọc tiếp
Đặt a = log2 3; b = log5 6. Tính T = log15 6 theo a, b.
![]()
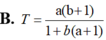
![]()
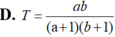
Tính giá trị của biểu thức sau: \(log^2_{\dfrac{1}{a}}a^2+log_{a^2}a^{\dfrac{1}{2}}\) (1≠a>0)
A. \(\dfrac{17}{4}\)
B. \(\dfrac{13}{4}\)
C. \(-\dfrac{11}{4}\)
D. -\(\dfrac{15}{4}\)
\(=\left(log_{a^{-1}}a^2\right)^2+\dfrac{1}{2}.\dfrac{1}{2}log_aa\)
\(=\left(-1.2.log_aa\right)^2+\dfrac{1}{4}=4+\dfrac{1}{4}=\dfrac{17}{4}\)
Đúng 0
Bình luận (0)
Đặt \({\log _2}5 = a,{\log _3}5 = b\). Khi đó, \({\log _6}5\) tính theo \(a\) và \(b\) bằng
A. \(\frac{{ab}}{{a + b}}\).
B. \(\frac{1}{{a + b}}\).
C. \({a^2} + {b^2}\).
D. \(a + b\).
\(log_65=\dfrac{1}{log_56}=\dfrac{1}{log_52+log_53}=\dfrac{1}{a+b}\)
=>Chọn B
Đúng 0
Bình luận (0)





