Đáp án B

chắc như mọi người nói

a: vecto AB=(1;3)

vecto AC=(9;-3)

Vì vecto AB*vecto AC=1*9+3*(-3)=0

nên ΔABC vuông tại A

b: ABCD là hình chữ nhật

=>vecto AB=vecto DC

=>10-x=1 và -2-y=3

=>x=9 và y=-5

\(C\in CK\Rightarrow C\left(x;-\dfrac{3}{8}x-\dfrac{13}{8}\right)\)

\(\Rightarrow\overrightarrow{BC}=\left(x+4;-\dfrac{3}{8}x-\dfrac{53}{8}\right)\)

AH có VTPT là \(\overrightarrow{n}=\left(5;3\right)\)

Do \(AH\) vuông góc \(BC\Rightarrow\overrightarrow{BC}=k\overrightarrow{n}\)

\(\Rightarrow\left\{{}\begin{matrix}x+4=5k\\-\dfrac{3}{8}x-\dfrac{53}{8}=3k\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{361}{39}\\k=-\dfrac{41}{39}\end{matrix}\right.\Rightarrow C\left(-\dfrac{361}{39};\dfrac{24}{13}\right)\).

\(A\in AH\Rightarrow A\left(x;-\dfrac{5}{3}x+\dfrac{4}{3}\right)\)

\(\Rightarrow\overrightarrow{BA}=\left(x+4;-\dfrac{5}{3}x-\dfrac{11}{3}\right)\)

\(CK\) có VTPT \(\overrightarrow{n}=\left(3;8\right)\)

Do \(CK\) vuông góc \(AB\Rightarrow\overrightarrow{BA}=k\overrightarrow{n}\)

\(\Rightarrow\left\{{}\begin{matrix}x+4=3k\\-\dfrac{5}{3}x-\dfrac{11}{3}=8k\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{43}{13}\\k=\dfrac{3}{13}\end{matrix}\right.\Rightarrow A\left(-\dfrac{43}{13};\dfrac{89}{13}\right)\).

*  Do đỉnh C thuộc trục Ox nên C(a;0). 

G thuộc trục Oy nên G(0; b).

* G là trọng tâm tam giác ABC  nên:

x G = x A + ​ x B + ​ x C 3 y G = y A + ​ y B + ​ y C 3 ⇒ 0 = − 2 + ​ 6 + ​ a 3 b = 2 + ​ ( − 4 ) + ​ 0 3 ⇔ a = − 4 b = − 2 3

Tọa độ trọng tâm tam giác ABC là  G ​ 0 ;    − 2 3

Đáp án B

Bạn coi lại đề, 2 đường thẳng xuất phát từ B nhưng lại song song với nhau, điều này hoàn toàn vô lý

Tham khảo:

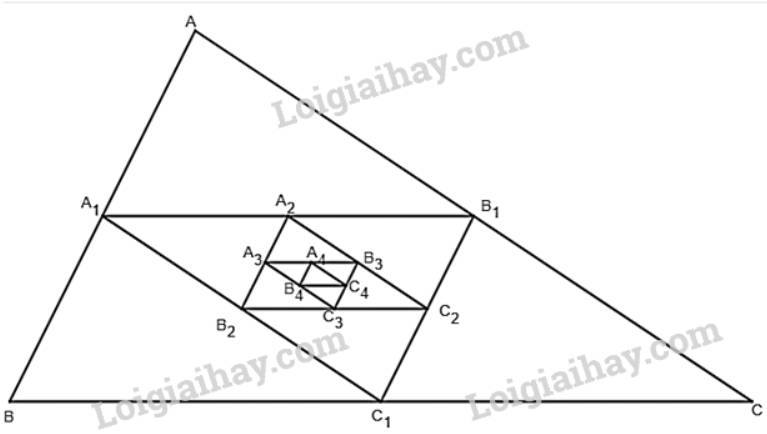
+) \(\left( {{{\rm{p}}_{\rm{n}}}} \right)\) là dãy số chu vi của các tam giác theo thứ tự \({\rm{ABC}},{{\rm{A}}_1}\;{{\rm{B}}_1}{{\rm{C}}_1}, \ldots \)

Ta có:

 \({{\rm{p}}_2} = {p_{\Delta {A_1}{B_1}{C_1}}} = \frac{a}{2} + \frac{a}{2} + \frac{a}{2} = \frac{1}{2} \cdot (3a) = \frac{1}{2} \cdot {p_1}\)

\(\begin{array}{l}{{\rm{p}}_3} = {p_{\Delta {A_2}{B_2}{C_2}}} = \frac{a}{4} + \frac{a}{4} + \frac{a}{4} = {\left( {\frac{1}{2}} \right)^2} \cdot (3a) = {\left( {\frac{1}{2}} \right)^2} \cdot {p_1}\\ \ldots \\{p_{\Delta {A_n}{B_n}{C_n}}} = {\left( {\frac{1}{2}} \right)^{n - 1}} \cdot {p_1}\\...\end{array}\)

\( \Rightarrow \mathop {\lim }\limits_{n \to \infty } {p_n} = \mathop {\lim }\limits_{n \to \infty } \left( {{{\left( {\frac{1}{2}} \right)}^{n - 1}} \cdot (3a)} \right) = \mathop {\lim }\limits_{n \to \infty } {\left( {\frac{1}{2}} \right)^{n - 1}} \cdot \mathop {\lim }\limits_{n \to \infty } (3a) = 0.3a = 0.\)

+)\(\left( {{{\rm{S}}_n}} \right)\) là dãy số diện tích của các tam giác theo thứ tự \({\rm{ABC}},{{\rm{A}}_1}\;{{\rm{B}}_1}{{\rm{C}}_1}, \ldots \)

Gọi \(h\) là chiều cao của tam giác \({\rm{ABC}}\) và \({\rm{h}} = \frac{{a\sqrt 3 }}{2}\).

Ta có:

\(\begin{array}{l}{{\rm{S}}_3} = {S_{\Delta {A_2}{B_2}{C_2}}} = \frac{1}{2} \cdot \frac{a}{4} \cdot \frac{h}{4} = {\left( {\frac{1}{4}} \right)^2} \cdot \left( {\frac{1}{2}ah} \right) = {\left( {\frac{1}{4}} \right)^2} \cdot {S_1}\\ \ldots \\{S_{\Delta {A_n}{B_n}{C_n}}} = {\left( {\frac{1}{4}} \right)^{n - 1}} \cdot {S_1}\\ \ldots \end{array}\)

\( \Rightarrow \mathop {\lim }\limits_{n \to \infty } {S_n} = \mathop {\lim }\limits_{n \to \infty } \left( {{{\left( {\frac{1}{4}} \right)}^{n - 1}} \cdot {S_1}} \right) = \mathop {\lim }\limits_{n \to \infty } {\left( {\frac{1}{4}} \right)^{n - 1}} \cdot \mathop {\lim }\limits_{n \to \infty } \left( {\frac{1}{2}ah} \right) = 0 \cdot \frac{1}{2}ah = 0\).

b) +) Ta có \(\left( {{{\rm{p}}_{\rm{n}}}} \right)\) là một cấp số nhân lùi vô hạn với số hạng đầu \({{\rm{p}}_1}\) = 3a và công bội \({\rm{q}} = \frac{1}{2}\) thỏa mãn \(|q| < 1\) có tổng:

\({p_1} + {p_2} +  \ldots  + {p_n} +  \ldots  = \frac{{3a}}{{1 - \frac{1}{2}}} = 6a\)

+) Ta có \(\left( {{{\rm{S}}_n}} \right)\) là một cấp số nhân lùi vô hạn với số hạng đầu \({{\rm{S}}_1} = \frac{1}{2}ah\) và công bội \(q = \frac{1}{4}\) thỏa mãn \(|q| < 1\) có tổng:

\({S_1} + {S_2} +  \ldots  + {S_n} +  \ldots  = \frac{{\frac{1}{2}ah}}{{1 - \frac{1}{4}}} = \frac{2}{3}ah = \frac{2}{3}a.\frac{{a\sqrt 3 }}{2} = \frac{{{a^2}\sqrt 3 }}{3}\)

Theo tính chất góc ngoài tam giác = tổng 2 góc trong không kề với nó. 

Ta có 

( B + C ):( A + C ):( A + B ) = 4:5:6 

=> ( B + C )/4 = ( A + C )/5 = ( A + B )/6 

Theo tính chất tỉ lệ thức kết hợp với tổng 3 góc trong tam giác = 360 độ. 

=> ( B + C )/4 = ( B + C + A + C + A + B )/( 4 + 5 + 6 ) = 360/15 = 24 

=> B + C = 96 (1) 

Tương tự ta có 

A + C = 120 (2) 

A + B = 144 (3) 

Kết hợp (1);(2);(3) ta có 

A = 84; B = 60; C = 36 

=> A:B:C = 84:60:36 = 7:5:3

I. Nội qui tham gia "Giúp tôi giải toán"

1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;

2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.

3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.

Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.