Tại sao x^2-16>0 lại bằng x>4;x
TC
Những câu hỏi liên quan
căn (5x-4)=2-x tại sao không đặt đk là 5x-4>=0 mà lại đặt 2-x>=0
Xem chi tiết
Pt xác định khi:
\(\left\{{}\begin{matrix}5x-4\ge0\\2-x\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{4}{5}\\x\le2\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{4}{5}\le x\le2\)
Nhưng trong TH này cậu phải làm cả hai nhé !
Đúng 1
Bình luận (0)
\(\sqrt[]{5x-4}=2-x\)
Phải lấy điều kiện \(2-x\ge0\) vì phương trình trên có dạng :
\(\sqrt[]{A}=B\) nên khi đặt điều kiện \(B\ge0\) thì chắc chắn \(\sqrt[]{A}\ge0\)
Nên không cần điều kiện \(A\ge0\) mà chỉ cần điều kiện \(B\ge0\) hay \(2-x\ge0\) là đủ.
Đúng 0
Bình luận (2)
1.Tìm giá trị của x sao cho hai biểu thức có giá trị bằng nhau: 0,35x+3/4x và 4+x/10+x-39
2.Tìm giá trị của x sao cho biểu thức sau có giá trị bằng 6: (1+x)^3+(1-x)^3-6x(x+1)
3. Giải các phương trình sau:
a,,(7x-2x)(2x-1)(x+3)=0
b,(4x-1)(x-3)-(x-3)(5x+2)=0
c, (x+4)(5x+9)-x^2+16=0
Bài 2:
(1 + x)3 + (1 - x)3 - 6x(x + 1) = 6
<=> x3 + 3x2 + 3x + 1 - x3 + 3x2 - 3x + 1 - 6x2 - 6x = 6
<=> -6x + 2 = 6
<=> -6x = 6 - 2
<=> -6x = 4
<=> x = -4/6 = -2/3
Bài 3:
a) (7x - 2x)(2x - 1)(x + 3) = 0
<=> 10x3 + 25x2 - 15x = 0
<=> 5x(2x - 1)(x + 3) = 0
<=> 5x = 0 hoặc 2x - 1 = 0 hoặc x + 3 = 0
<=> x = 0 hoặc x = 1/2 hoặc x = -3
b) (4x - 1)(x - 3) - (x - 3)(5x + 2) = 0
<=> 4x2 - 13x + 3 - 5x2 + 13x + 6 = 0
<=> -x2 + 9 = 0
<=> -x2 = -9
<=> x2 = 9
<=> x = +-3
c) (x + 4)(5x + 9) - x2 + 16 = 0
<=> 5x2 + 9x + 20x + 36 - x2 + 16 = 0
<=> 4x2 + 29x + 52 = 0
<=> 4x2 + 13x + 16x + 52 = 0
<=> 4x(x + 4) + 13(x + 4) = 0
<=> (4x + 13)(x + 4) = 0
<=> 4x + 13 = 0 hoặc x + 4 = 0
<=> x = -13/4 hoặc x = -4
Lê Nhật Hằng cảm ơn bạn nha
Tại sao khi giải pt asin²x +bsinxcosx +c.cos²x=d thì lại đặt cosx bằng 0 nữa vậy ạ. Mình chỉ đặt cos x khác 0 là được mà.
Như vậy sẽ có rất nhiều trường hợp thiếu nghiệm, đó là khi \(a=d\) (mất 1/2 số điểm đó em)
Ví dụ: giải phương trình
\(2sin^2x+3sinx.cosx+cos^2x=2\)
Trường hợp này ko xét \(cosx=0\) là mất nửa số điểm rồi (mất hẳn 1 họ nghiệm)
Đúng 1
Bình luận (0)
Cho phân thức A= x²+8x+16/ x²-16 a) Tìm điều kiện xác định của A. b) Rút gọn phân thức. c) Tìm giá trị của x để phân thức A có giá trị bằng 3. d ) Có giá trị nào của x để giá trị của phân thức A bằng 0 hay không? Tại sao?
Lời giải:
a. ĐKXĐ: $x^2-16\neq 0\Leftrightarrow (x-4)(x+4)\neq 0$
$\Leftrightarrow x\neq \pm 4$
b. $A=\frac{x^2+8x+16}{x^2-16}=\frac{(x+4)^2}{(x-4)(x+4)}=\frac{x+4}{x-4}$
c. $A=3\Leftrightarrow \frac{x+4}{x-4}=3$
$\Rightarrow x+4=3(x-4)$
$\Leftrightarrow -2x+16=0$
$\Leftrightarrow x=8$ (tm)
d.
$A=0\Leftrightarrow \frac{x+4}{x-4}=0\Leftrightarrow x+4=0\Leftrightarrow x=-4$
Mà theo ĐKXĐ thì $x\neq \pm 4$ nên không tồn tại $x$ để $A=0$
Đúng 2
Bình luận (0)
Với x>0, GTNN của biểu thức
\(A=\dfrac{\left(x+16\right)\left(x+9\right)}{x}\) là ...... (tại sao kq lại là 49 ak??)
Thank you very very much!!!
BĐT AM-GM để xem à
\(A=\dfrac{\left(x+16\right)\left(x+9\right)}{x}=\dfrac{x^2+25x+144}{x}=x+25+\dfrac{144}{x}\)
Áp dụng BĐT AM-GM cho 2 số không âm
\(x+\dfrac{144}{x}\ge2\sqrt{\dfrac{x.144}{x}}\)
\(x+\dfrac{144}{x}\ge24\)
\(x+\dfrac{144}{x}+25\ge49\)
\(A\ge49\)
\(Min_A=49\)
Đúng 0
Bình luận (0)
\(A=\dfrac{x^2+25x+\left(3.4\right)^2}{x}=\dfrac{x^2+\left[49x-24x\right]+\left(3.4\right)^2}{x}=\dfrac{x^2-24x+\left(3.4\right)^2+49x}{x}\)\(A=\dfrac{\left(x-12\right)^2}{x}+49\ge49\)
Đúng 0
Bình luận (0)
Rút gọn biểu thức B=(√x/√x+4 + 4/√x-4) : x+16/√x+2 ( với x lớn hơn hoặc bằng 0; x#16)
Ta có: \(B=\left(\frac{\sqrt{x}}{\sqrt{x}+4}+\frac{4}{\sqrt{x}-4}\right):\frac{x+16}{\sqrt{x}+2}\)
\(=\left(\frac{\sqrt{x}\left(\sqrt{x}-4\right)}{\left(\sqrt{x}+4\right)\left(\sqrt{x}-4\right)}+\frac{4\left(\sqrt{x}+4\right)}{\left(\sqrt{x}-4\right)\left(\sqrt{x}+4\right)}\right)\cdot\frac{\sqrt{x}+2}{x+16}\)
\(=\frac{x-4\sqrt{x}+4\sqrt{x}+16}{\left(\sqrt{x}-4\right)\left(\sqrt{x}+4\right)}\cdot\frac{\sqrt{x}+2}{x+16}\)
\(=\frac{x+16}{x-16}\cdot\frac{\sqrt{x}+2}{x+16}\)
\(=\frac{\sqrt{x}+2}{x-16}\)
Đúng 0
Bình luận (0)
a) C = ( x - 1).( x - 2).( 3 - x). Tìm x sao cho C < 0
b) D = ( x^2 - 4). ( 16 - x^2 ). Tìm x sao cho D > hoặc = 0
cái này dùng bảng xét dấu là nhanh nhất. mình làm mẫu cho một cái, bạn xem rồi tự tìm hiểu nha. nếu vẫn k hiểu thì liên hệ mình giải nốt cho. bảng xét dấu này lấy nghiệm của từng nhân tử rồi theo quy tắc phải cùng, trái khác để xét dấu
D= (x-2)(x+2).(4-x)(4+x)
a) C<0
nhìn bảng xét dấu ta có thể thấy rằng tích này âm trong 2 trường hợp: \(1\le x\le2\)và x>3
tương tự làm với câu 2 nha
Đúng 0
Bình luận (0)
a) C = ( x - 1).( x - 2).( 3 - x). Tìm x sao cho C < 0
b) D = ( x^2 - 4). ( 16 - x^2 ). Tìm x sao cho D > hoặc = 0
a) C < 0 <=>
hoặc x - 1 < 0 => x < 1
hoặc x - 2 < 0 => x < 2
hoặc x - 3 < 0 => x < 3
Vậy x < 3 thỏa mãn đề bài.
Đúng 0
Bình luận (0)
Chỉ mình chỗ khoanh tròn màu đỏ: + Tại sao ra 2 trường hợp 0x1 ; x1 + dfrac{1}{sqrt{x}-1}le-1 ( làm sao ra được như này) + sqrt{x}-10 có phải từ x1 rồi lấy căn 2 vế rồi chuyển vế đúng không + Và tại sao gọi là hàm số và tại sao lại không tìm được GTLN + Còn GTNN thì sẽ như thế nào
Đọc tiếp
Chỉ mình chỗ khoanh tròn màu đỏ:
+ Tại sao ra 2 trường hợp 0<x<1 ; x>1
+ \(\dfrac{1}{\sqrt{x}-1}\le-1\) ( làm sao ra được như này)
+ \(\sqrt{x}-1>0\) có phải từ x>1 rồi lấy căn 2 vế rồi chuyển vế đúng không
+ Và tại sao gọi là hàm số và tại sao lại không tìm được GTLN
+ Còn GTNN thì sẽ như thế nào
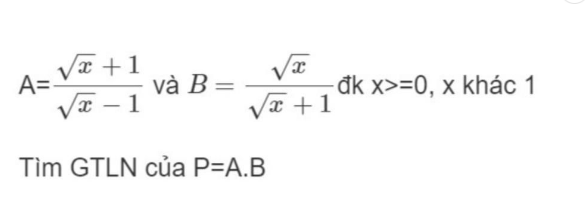

Đơn giản là em đang xem một lời giải sai. Việc khẳng định $P\leq 0$ hoặc $P>0$ rồi kết luận hàm số không có GTLN là sai.
Bởi vậy những câu hỏi ở dưới là vô nghĩa.
Việc gọi $P$ là hàm số lên lớp cao hơn em sẽ được học, còn bây giờ chỉ cần gọi đơn giản là phân thức/ biểu thức.
Hàm số, có dạng $y=f(x)$ biểu diễn mối liên hệ giữa biến $x$ với biến phụ thuộc $y$. Mỗi giá trị của $x$ ta luôn xác định được một giá trị tương ứng của $y$.
Đúng 0
Bình luận (0)
$P=AB=\frac{\sqrt{x}}{\sqrt{x}-1}=1+\frac{1}{\sqrt{x}-1}$
Để $P_{\max}$ thì $\frac{1}{\sqrt{x}-1}$ max
Điều này xảy ra khi $\sqrt{x}-1$ min và có giá trị dương
$\Leftrightarrow x>1$ và $x$ nhỏ nhất
Trong tập số thực thì em không thể tìm được số lớn hơn 1 mà nhỏ nhất được. Như kiểu $1,00000000000000000000....$ (vô hạn đến không biết khi nào thì kết thúc)
Do đó $P$ không có max
Min cũng tương tự, $P$ không có min.
Đúng 0
Bình luận (3)



