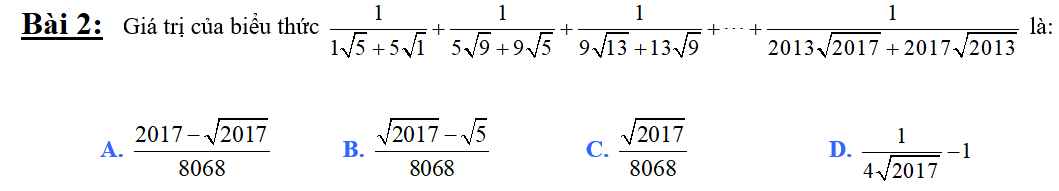
Làm chi tiết giúp e với ạ
MN GIÚP E CÂU 5 VỚI Ạ. GIẢI CHI TIẾT CÁCH LÀM DÙM E VỚI Ạ.

Câu 5:
\(\Leftrightarrow-x^2+7x-9+2x-9=0\)
\(\Leftrightarrow x^2-9x+18=0\)
=>x=3
=>Chọn A
Giúp e làm chi tiết với ạ
câu 27 cái đầu là on cái sau là in
28B
21. đúng ra là any of those who
bạn chọn B
MN GIÚP E BÀI 2,7,8 VỚI Ạ. GIẢI CHI TIẾT CÁCH LÀM DÙM E.
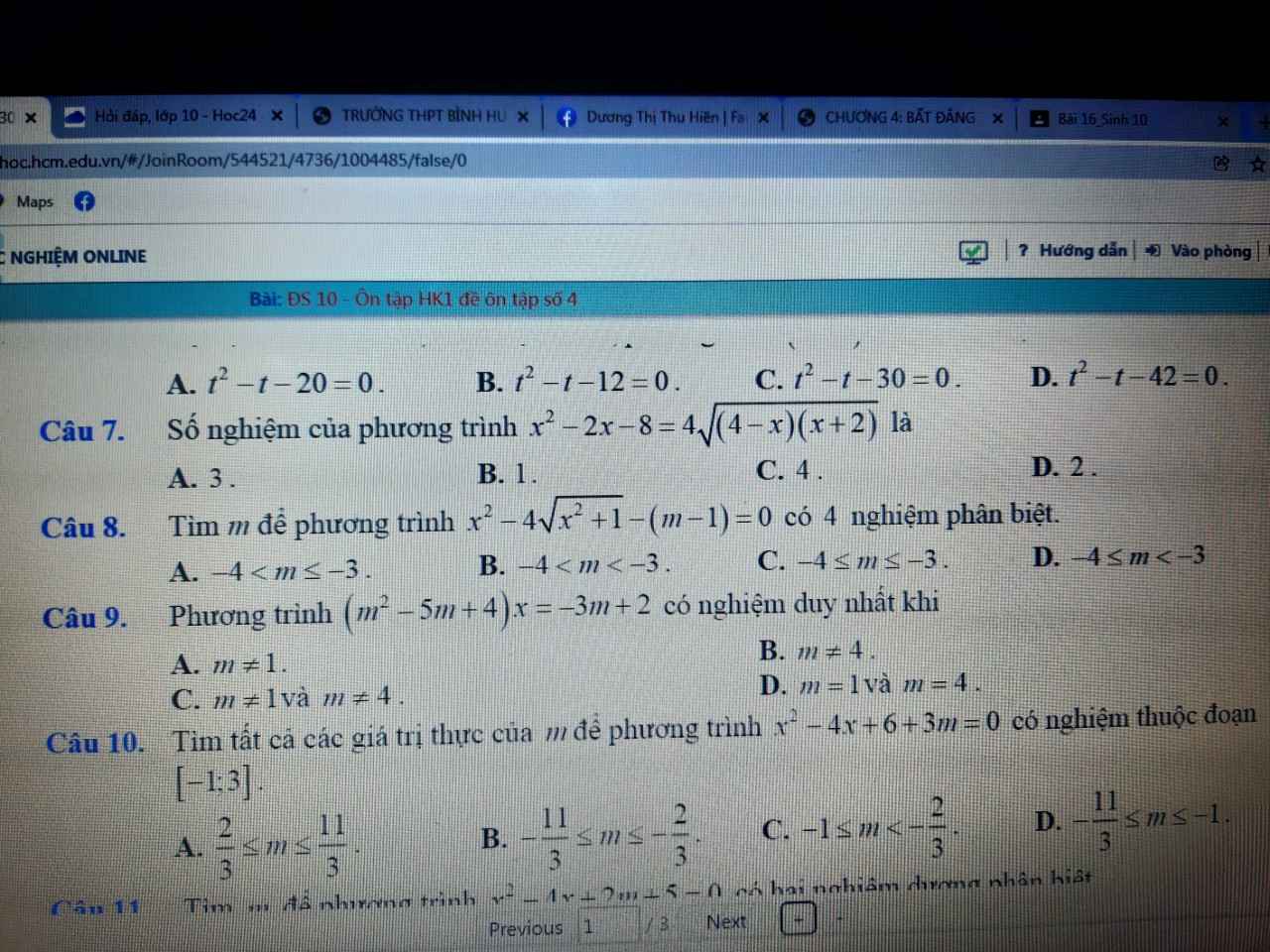
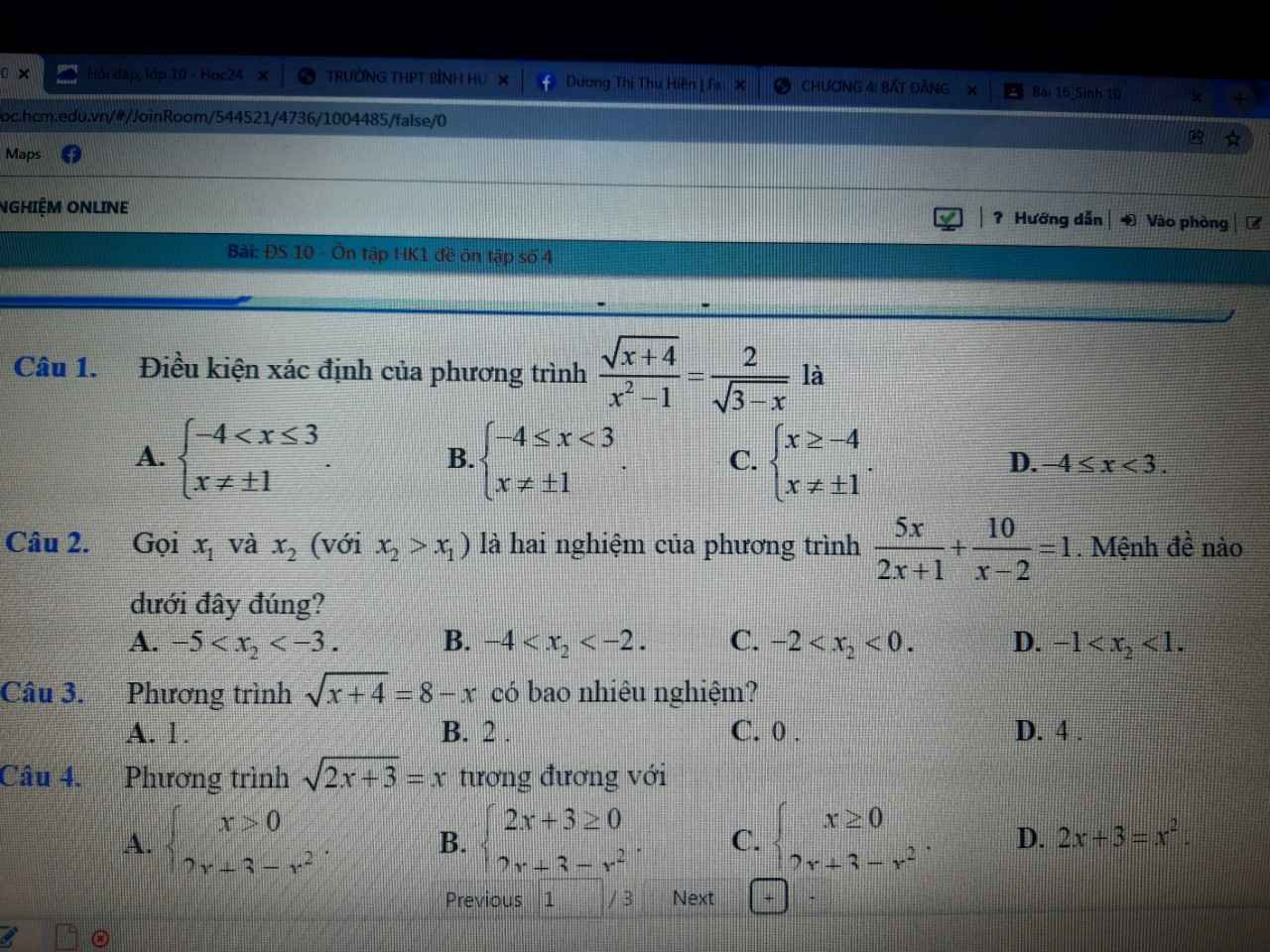
Hhduwhbsbbsxhhdjzbe ủbxuhxuenxurbxurn run ư nếu xiên Yến rũ EU. Hẹn
rung bình có phương và chiều trùng với vectơ độ dời
loading...
Độ lớn của vận tốc trung bình được tính như sau:
∣
v
t
b
→
∣
=
∣
Δ
r
→
∣
Δ
t
=
12
1
=
12
∣
v
tb
∣=
Δt
∣
Δr
∣
=
1
12
=12 (m/s)
(Do tam giác tạo bởi các vectơ
r
1
→
,
r
2
→
,
Δ
r
→
r
1
,
r
2
,
Δr
đều)
Đúng(18)
giải chi tiết câu 16 đầu tiên cách làm và đáp án giúp e với ạ e đang cần gấp
Ta có : \(f\left(2\right)=2a+b-6\)
\(\lim\limits_{x\rightarrow2^+}\dfrac{x-\sqrt{x+2}}{x^2-4}=\lim\limits_{x\rightarrow2^+}\dfrac{x^2-x-2}{\left(x-2\right)\left(x+2\right)\left(x+\sqrt{x+2}\right)}\)
\(=\lim\limits_{x\rightarrow2^+}\dfrac{x+1}{\left(x+2\right)\left(x+\sqrt{x+2}\right)}=\dfrac{3}{16}\)
\(\lim\limits_{x\rightarrow2^-}x^2+ax+3b=4+2a+3b\)
H/s liên tục tại điểm x = 2 \(\Leftrightarrow\dfrac{3}{16}=2a+3b+4=2a+b-6\)
Suy ra : \(a=\dfrac{179}{32};b=-5\) => t = a + b = 19/32 . Chọn C
Giúp e làm câu 8 chi tiết đi ạ
\(f\left(x\right)=x^5+x^3\Rightarrow f'\left(x\right)=5x^4+3x^2\)
\(f'\left(2\right)=5.2^4+3.2^2=92\)
\(f\left(x\right)=x^5+x^3\)
=>\(f'\left(x\right)=5x^4+3x^2\)
=>\(f'\left(2\right)=5.2^4+3.2^2\)
\(f'\left(2\right)=5.16+3.4=92\)
Giúp e làm chi tiết câu 21, 22 đi ạ
21.
Giới hạn đã cho hữu hạn khi và chỉ khi \(a=1\)
Khi đó:
\(\lim\limits_{x\rightarrow+\infty}\left(x-\sqrt{x^2+bx+2}\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{x^2-\left(x^2+bx+2\right)}{x+\sqrt{x^2+bx+2}}=\lim\limits_{x\rightarrow+\infty}\dfrac{-bx-2}{x+\sqrt{x^2+bx+2}}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{-b-\dfrac{2}{x}}{1+\sqrt{1+\dfrac{b}{x}+\dfrac{2}{x^2}}}=\dfrac{-b}{2}\)
\(\Rightarrow-\dfrac{b}{2}=4\Rightarrow b=-8\)
\(\Rightarrow a+b=1-8=-7\)
22.
B sai, do các cạnh bên của chóp đều tạo với đáy các góc bằng nhau
 vẽ hình với làm chi tiết giúp ạ e cảm ơn gấp 15 phú nữa là phải báo cáo vơiz cô rôid
vẽ hình với làm chi tiết giúp ạ e cảm ơn gấp 15 phú nữa là phải báo cáo vơiz cô rôid
a: ΔABC vuông tại A
mà AM là trung tuyến
nên MA=MB=MC=BC/2
Xét ΔMAB có MA=MB và \(\widehat{MBA}=60^0\)
nên ΔMAB đều
b: ΔBAM đều
mà BH là đường cao
nên H là trung điểm của AM
Xét ΔHNM vuông tại H và ΔHBA vuông tại H có
HM=HA
\(\widehat{HMN}=\widehat{HAB}\)(MN//AB)
Do đó: ΔHNM=ΔHBA
=>HN=HB
=>H là trung điểm của BN
Xét tứ giác ABMN có
H là trung điểm chung của AM và BN
BM=BA
Do đó: ABMN là hình thoi
c: ABMN là hình thoi
=>\(\widehat{NMB}=180^0-\widehat{MBA}=180^0-60^0=120^0\)
Xét ΔMNB có \(cosNMB=\dfrac{MN^2+MB^2-BN^2}{2\cdot MN\cdot MB}\)
\(\Leftrightarrow\dfrac{AB^2+AB^2-BN^2}{2\cdot AB\cdot AB}=-\dfrac{1}{2}\)
=>\(2AB^2-BN^2=-AB^2\)
=>\(BN^2=3AB^2\)
Xét ΔMAC có \(cosAMC=\dfrac{MA^2+MC^2-AC^2}{2\cdot MA\cdot MC}\)
=>\(\dfrac{AB^2+AB^2-AC^2}{2\cdot AB\cdot AB}=cos120=\dfrac{-1}{2}\)
=>\(2AB^2-AC^2=-AB^2\)
=>\(AC^2=3AB^2\)
=>\(AC^2=BN^2\)
=>AC=BN
Giúp e giải chi tiết với ạ e cảm ơn ạ
Bài 1
a,\(\dfrac{x}{3}\)=\(\dfrac{20}{y}\)=4
b,\(\dfrac{9}{-x}\)=\(\dfrac{y}{5}\)=-3
Mọi người làm chi tiết giúp e với ạ
\(a.\dfrac{12}{3}=\dfrac{20}{5}=4\\ b.\dfrac{9}{-3}=\dfrac{-15}{5}=-3\)
a, Xét \(\dfrac{x}{3}=4\Rightarrow x=12;\dfrac{20}{y}=4\Rightarrow y=\dfrac{20}{4}=5\)
b, \(\dfrac{9}{-x}=-3\Rightarrow-x=-3\Leftrightarrow x=3\)
\(\dfrac{y}{5}=-3\Rightarrow y=-15\)