Cho ΔABC vuông tại A (AB < AC), M là trung điểm của BC. Gọi D là điểm đối xứng của A qua M. C) vẽ K đối xứng với A qua E. Chứng minh: K và D đối xứng qua B.
Bài 11: Hình thoi
làm chi tiết theo chương trình mới lớp 8 ạ
a: ΔABC vuông tại A
mà AM là đường trung tuyến
nên \(AM=MB=MC=\dfrac{BC}{2}\)
Xét ΔBAM có
MA=MB
Do đó: ΔBAM cân tại M
Xét ΔMAB cân tại M có \(\widehat{MBA}=60^0\)
nên ΔMAB đều
b: ΔMAB đều
mà BH là đường cao
nên H là trung điểm của AM
Xét ΔHMN vuông tại H và ΔHAB vuông tại H có
HA=HM
\(\widehat{HMN}=\widehat{HAB}\)
Do đó: ΔHMN=ΔHAB
=>HN=HB
Xét tứ giác ABMN có
H là trung điểm chung của AM và BN
nên ABMN là hình bình hành
=>AN//MB và AN=MB
AN=MB
MB=MC
Do đó: AN=MC
AN//MB
\(M\in BC\)
Do đó: AN//MC
Xét tứ giác AMCN có
AN//CM
AN=CM
Do đó: AMCN là hình bình hành
Hình bình hành AMCN có AC\(\perp\)MN
nên AMCN là hình thoi
c: ABMN là hình bình hành
=>\(\widehat{NMB}+\widehat{MBA}=180^0\)
=>\(\widehat{NMB}=120^0\)
Hình bình hành ABMN có NB\(\perp\)AM
nên ABMN là hình thoi
Xét ΔNMB có \(\dfrac{NB}{sinNMB}=\dfrac{BM}{sinMNB}\)
=>\(\dfrac{NB}{sin120}=\dfrac{BM}{sin30}\)
=>\(NB=BM\cdot\sqrt{3}\)
Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}\)
=>\(\dfrac{AC}{2\cdot BM}=sin60=\dfrac{\sqrt{3}}{2}\)
=>\(AC=BM\cdot\sqrt{3}\)
=>AC=NB
Đúng 1
Bình luận (0)
vẽ hình với làm chi tiết giúp ạ e cảm ơn gấp 15 phú nữa là phải báo cáo vơiz cô rôid
a: ΔABC vuông tại A
mà AM là trung tuyến
nên MA=MB=MC=BC/2
Xét ΔMAB có MA=MB và \(\widehat{MBA}=60^0\)
nên ΔMAB đều
b: ΔBAM đều
mà BH là đường cao
nên H là trung điểm của AM
Xét ΔHNM vuông tại H và ΔHBA vuông tại H có
HM=HA
\(\widehat{HMN}=\widehat{HAB}\)(MN//AB)
Do đó: ΔHNM=ΔHBA
=>HN=HB
=>H là trung điểm của BN
Xét tứ giác ABMN có
H là trung điểm chung của AM và BN
BM=BA
Do đó: ABMN là hình thoi
c: ABMN là hình thoi
=>\(\widehat{NMB}=180^0-\widehat{MBA}=180^0-60^0=120^0\)
Xét ΔMNB có \(cosNMB=\dfrac{MN^2+MB^2-BN^2}{2\cdot MN\cdot MB}\)
\(\Leftrightarrow\dfrac{AB^2+AB^2-BN^2}{2\cdot AB\cdot AB}=-\dfrac{1}{2}\)
=>\(2AB^2-BN^2=-AB^2\)
=>\(BN^2=3AB^2\)
Xét ΔMAC có \(cosAMC=\dfrac{MA^2+MC^2-AC^2}{2\cdot MA\cdot MC}\)
=>\(\dfrac{AB^2+AB^2-AC^2}{2\cdot AB\cdot AB}=cos120=\dfrac{-1}{2}\)
=>\(2AB^2-AC^2=-AB^2\)
=>\(AC^2=3AB^2\)
=>\(AC^2=BN^2\)
=>AC=BN
Đúng 0
Bình luận (0)
ve so do hinh thoi! giai ho mik aj
Cho tam giác ABC có AD là đường phân giác.Từ D kẻ DM//AC (M thuộc AB,N thuộc AC,DN//AB)
CM:Tứ giác AMDN là hình thoi
Xét tứ giác AMDN có
AM//DN
AN//DM
Do đó: AMDN là hình bình hành
Hình bình hành AMDN có AD là phân giác của \(\widehat{MAN}\)
nên AMDN là hình thoi
Đúng 1
Bình luận (0)
cho tam giác ABC kẻ đường cao BD và CE trên tia đối của DB lấy DM=DB.Trên tia đối của tia CE lấy EN=CE.chứng minh tứ giác ABCM và ACBN là hình thoi
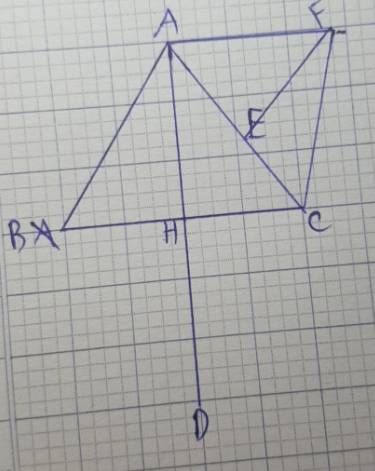
mong mọi người giúp đỡ tôi bài này với , nếu sai hình thì mong mọi người sửa lại giúp cho , xin chân thành cảm ơn
a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
Xét tứ giác ABDC có
H là trung điểm chung của AD và BC
nên ABDC là hình bình hành
Hình bình hành ABDC có AB=AC
nên ABDC là hình thoi
b: H là trung điểm của BC
=>\(HB=HC=\dfrac{BC}{2}=3\left(cm\right)\)
ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AH^2=5^2-3^2=16\)
=>AH=4(cm)
AD=2*AH
=>AD=2*4=8(cm)
c:
Xét tứ giác AHCF có
E là trung điểm chung của AC và HF
nên AHCF là hình bình hành
Hình bình hành AHCF có \(\widehat{AHC}=90^0\)
nên AHCF là hình chữ nhật
=>AH\(\perp\)AF và HC\(\perp\)FC
d: ABDC là hình thoi
=>\(\widehat{BAC}=\widehat{BDC}=60^0\)
ABDC là hình thoi
=>\(\widehat{ABD}+\widehat{BAC}=180^0\)
=>\(\widehat{ABD}=120^0\)
ABDC là hình thoi
=>\(\widehat{ABD}=\widehat{ACD}=120^0\)
Đúng 0
Bình luận (0)
mong mọi người giúp đỡ tôi bài này với , nếu sai hình thì mong mọi người sửa lại giúp cho , xin chân thành cảm ơn
a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
Xét tứ giác ABDC có
H là trung điểm chung của AD và BC
nên ABDC là hình bình hành
Hình bình hành ABDC có AB=AC
nên ABDC là hình thoi
b: H là trung điểm của BC
=>\(HB=HC=\dfrac{BC}{2}=3\left(cm\right)\)
ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AH^2=5^2-3^2=16\)
=>AH=4(cm)
AD=2*AH
=>AD=2*4=8(cm)
c:
Xét tứ giác AHCF có
E là trung điểm chung của AC và HF
nên AHCF là hình bình hành
Hình bình hành AHCF có \(\widehat{AHC}=90^0\)
nên AHCF là hình chữ nhật
=>AH\(\perp\)AF và HC\(\perp\)FC
d: ABDC là hình thoi
=>\(\widehat{BAC}=\widehat{BDC}=60^0\)
ABDC là hình thoi
=>\(\widehat{ABD}+\widehat{BAC}=180^0\)
=>\(\widehat{ABD}=120^0\)
ABDC là hình thoi
=>\(\widehat{ABD}=\widehat{ACD}=120^0\)
Đúng 0
Bình luận (0)
a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
Xét tứ giác ABDC có
H là trung điểm chung của AD và BC
nên ABDC là hình bình hành
Hình bình hành ABDC có AB=AC
nên ABDC là hình thoi
b: H là trung điểm của BC
=>\(HB=HC=\dfrac{BC}{2}=3\left(cm\right)\)
ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AH^2=5^2-3^2=16\)
=>AH=4(cm)
AD=2*AH
=>AD=2*4=8(cm)
c:
Xét tứ giác AHCF có
E là trung điểm chung của AC và HF
nên AHCF là hình bình hành
Hình bình hành AHCF có \(\widehat{AHC}=90^0\)
nên AHCF là hình chữ nhật
=>AH\(\perp\)AF và HC\(\perp\)FC
d: ABDC là hình thoi
=>\(\widehat{BAC}=\widehat{BDC}=60^0\)
ABDC là hình thoi
=>\(\widehat{ABD}+\widehat{BAC}=180^0\)
=>\(\widehat{ABD}=120^0\)
ABDC là hình thoi
=>\(\widehat{ABD}=\widehat{ACD}=120^0\)
Đúng 0
Bình luận (0)