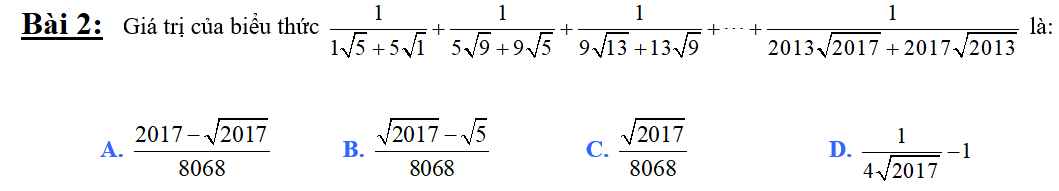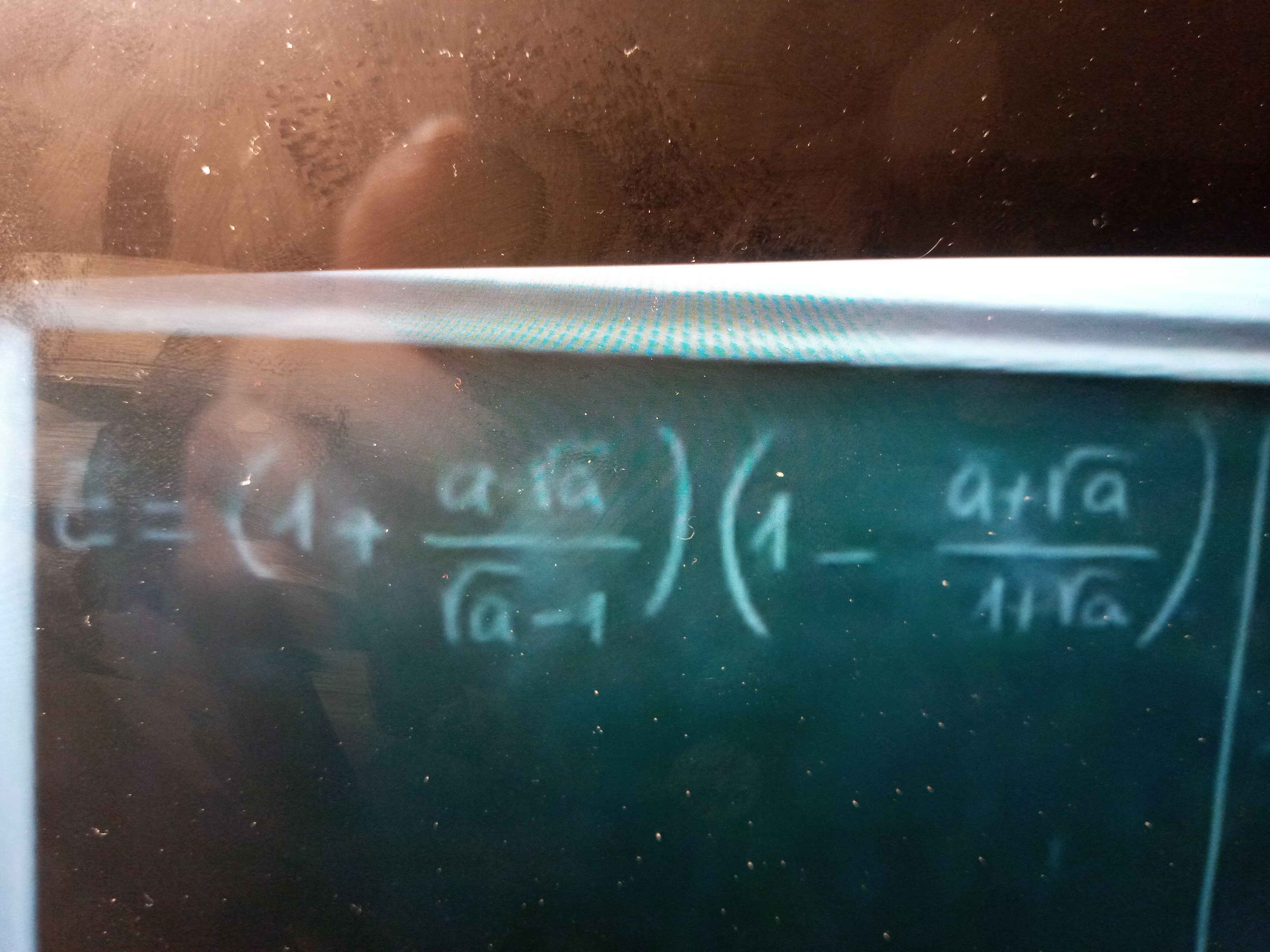Với \(n>0;n\in N:\dfrac{1}{n\sqrt{n+4}+\left(n+4\right)\sqrt{n}}=\dfrac{1}{\sqrt{n\left(n+4\right)}\left(\sqrt{n}+\sqrt{n+4}\right)}=\dfrac{\sqrt{n+4}-\sqrt{n}}{\sqrt{n\left(n+4\right)}\left(n+4-n\right)}=\dfrac{1}{4}\left(\dfrac{1}{\sqrt{n}}-\dfrac{1}{\sqrt{n+4}}\right)\) (1)
Áp dụng (1) ta được:
\(\dfrac{1}{1\sqrt{5}+5\sqrt{1}}+\dfrac{1}{5\sqrt{9}+9\sqrt{5}}+...+\dfrac{1}{2013\sqrt{2017}+2017\sqrt{2013}}\)
\(=\dfrac{1}{4}\left(1-\dfrac{1}{\sqrt{5}}+\dfrac{1}{\sqrt{5}}-\dfrac{1}{\sqrt{9}}+...+\dfrac{1}{\sqrt{2013}}-\dfrac{1}{\sqrt{2017}}\right)\)
\(=\dfrac{1}{4}\left(1-\dfrac{1}{\sqrt{2017}}\right)=\dfrac{\sqrt{2017}-1}{4\sqrt{2017}}=\dfrac{2017-\sqrt{2017}}{8068}\)
Ý A
Đúng 2
Bình luận (1)
