Cho phép tịnh tiến T\(\overrightarrow{v}\) có \(\overrightarrow{v}\)=(-2;3). Tìm m để phép tịnh tiến T\(\overrightarrow{v}\) biến d: mx-(m+1)y-2=0 thành chính nó
NM
Những câu hỏi liên quan
cho 2 phép tịnh tiến T\(\overrightarrow{u}\) và T\(\overrightarrow{v}\) . Với điểm M bất kỳ , T\(\overrightarrow{u}\) biến điểm thành điểm M' , T\(\overrightarrow{v}\) biến M' thành M'' . Chứng tỏ rằng phép biến hình biến M thành M'' là một phép tịnh tiến .
M-> M' => VÊCTỚ MM'= VT u
Tv: M' -> M'' => vt M'M'' = v
áp dụng quy tắc 3 diểm => vt MM' +M'M'' = u+v =w
=> với mỗi điểm M qua phép tt theo vecto w se biến M -> M'' => ĐÓ LÀ PHÉP TT
Đúng 0
Bình luận (0)
Cho vectơ overrightarrow{v}, đường thẳng d vuông góc với giá của overrightarrow{v}. Gọi d là ảnh của d qua phép tịnh tiến theo vectơ dfrac{1}{2}overrightarrow{v}. Chứng minh rằng phép tịnh tiến theo vectơ overrightarrow{v} là kết quả của việc thực hiện liên tiếp phép đối xứng qua các đường thẳng d và d ?
Đọc tiếp
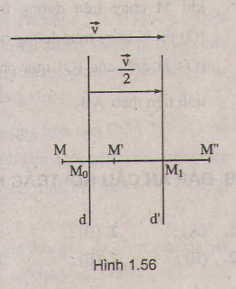
Cho vectơ \(\overrightarrow{v}\), đường thẳng d vuông góc với giá của \(\overrightarrow{v}\). Gọi d' là ảnh của d qua phép tịnh tiến theo vectơ \(\dfrac{1}{2}\overrightarrow{v}\). Chứng minh rằng phép tịnh tiến theo vectơ \(\overrightarrow{v}\) là kết quả của việc thực hiện liên tiếp phép đối xứng qua các đường thẳng d và d' ?
Lấy M tùy ý. Gọi (M) = M',
(M') = M''. Ta có
\(\overrightarrow{MM'}=\overrightarrow{MM'}+\overrightarrow{M'M''}=2\overrightarrow{M_oM'}+2\overrightarrow{M'M_1}=2\overrightarrow{M_oM_1}\)\(=2\dfrac{\overrightarrow{v}}{2}=\overrightarrow{v}\).
Vậy M'' = (M) =
(
(M)), với mọi M
Do đó phép tịnh tiến theo vectơ v là kết quả của việc thực hiện liên tiếp phép đối xứng qua các đường thẳng d và d'.
Đúng 0
Bình luận (0)
Trong mp Oxy cho \(\overrightarrow{v}\left(1;2\right)\), d: x - 3y + 6 = 0. Tìm ảnh của d qua phép dời hình có được bằng cách thực hiện liên tiếp phép tịnh tiến theo \(\overrightarrow{v}\) và phép quay tâm O góc \(\dfrac{-\pi}{2}\)
Trong mặt phẳng Oxy, cho elip (E): frac{x^2}{9}+frac{y^2}{4}1. Tìm phương trình của (E) là ảnh của (E) qua phép tịnh tiến theo véctơ overrightarrow{v} trong các trường hợp saua) overrightarrow{v}(4;-3)b) overrightarrow{v}(2;1)c) overrightarrow{v}(-2;1)
Đọc tiếp
Trong mặt phẳng Oxy, cho elip \((E): \frac{x^2}{9}+\frac{y^2}{4}=1\). Tìm phương trình của (E') là ảnh của (E) qua phép tịnh tiến theo véctơ \(\overrightarrow{v}\) trong các trường hợp sau
a) \(\overrightarrow{v}=(4;-3)\)
b) \(\overrightarrow{v}=(2;1)\)
c) \(\overrightarrow{v}=(-2;1)\)
Trong mặt phẳng tọa độ Oxy cho vectơ overrightarrow{v}left(-1;2right). Hai điểm Aleft(3;5right);Bleft(-1;1right) và đường thẳng d có phương trình x-2y+30
a) Tìm tọa độ của các điểm A, B theo thứ tự là ảnh của A, B qua phép tịnh tiến theo overrightarrow{v}
b) Tìm tọa độ của điểm C sao cho A là ảnh của C qua phép tịnh tiến theo overrightarrow{v}
c) Tìm phương trình của đường thẳng d là ảnh của d qua phép tịnh tiến theo overrightarrow{v}
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho vectơ \(\overrightarrow{v}=\left(-1;2\right)\). Hai điểm \(A\left(3;5\right);B\left(-1;1\right)\) và đường thẳng d có phương trình \(x-2y+3=0\)
a) Tìm tọa độ của các điểm A', B' theo thứ tự là ảnh của A, B qua phép tịnh tiến theo \(\overrightarrow{v}\)
b) Tìm tọa độ của điểm C sao cho A là ảnh của C qua phép tịnh tiến theo \(\overrightarrow{v}\)
c) Tìm phương trình của đường thẳng d' là ảnh của d qua phép tịnh tiến theo \(\overrightarrow{v}\)
a) Giả sử A'=(x'; y'). Khi đó \(T_{\overrightarrow{v}}\left(A\right)=A'\Leftrightarrow\left\{{}\begin{matrix}x'=3-1=2\\y'=5+2=7\end{matrix}\right.\)
Do đó: A' = (2;7)
Tương tự B' =(-2;3)
b) Ta có: \(A=T_{\overrightarrow{v}}\left(C\right)\Leftrightarrow C=^T\overrightarrow{-v}\left(A\right)=\left(4;3\right)\)
c) Cách 1. Dùng biểu thức tọa độ của phép tịnh tiến
Gọi M(x;y), M' = \(^T\overrightarrow{v}\) =(x'; y'). Khi đó x' = x-1, y' = y + 2 hay x = x' +1, y= y' - 2. Ta có M ∈ d ⇔ x-2y +3 = 0 ⇔ (x'+1) - 2(y'-2)+3=0 ⇔ x' -2y' +8=0 ⇔ M' ∈ d' có phương trình x-2y+8=0. Vậy \(^T\overrightarrow{v}\) (d) = d'.
Cách 2. Dùng tính chất của phép tịnh tiến
Gọi \(^T\overrightarrow{v}\)(d) =d'. Khi đó d' song song hoặc trùng với d nên phương trình của nó có dạng x-2y+C=0. Lấy một điểm thuộc d chẳng hạn B(-1;1), khi đó \(^T\overrightarrow{v}\) (B) = (-2;3) thuộc d' nên -2 -2.3 +C =0. Từ đó suy ra C = 8.
Đúng 0
Bình luận (0)
a) Giả sử A'=(x'; y'). Khi đó
(A) = A' ⇔
Do đó: A' = (2;7)
Tương tự B' =(-2;3)
b) Ta có A = (C) ⇔ C=
(A) = (4;3)
c)Cách 1. Dùng biểu thức tọa độ của phép tịnh tiến
Gọi M(x;y), M' = =(x'; y'). Khi đó x' = x-1, y' = y + 2 hay x = x' +1, y= y' - 2. Ta có M ∈ d ⇔ x-2y +3 = 0 ⇔ (x'+1) - 2(y'-2)+3=0 ⇔ x' -2y' +8=0 ⇔ M' ∈ d' có phương trình x-2y+8=0. Vậy
(d) = d'
Cách 2. Dùng tính chất của phép tịnh tiến
Gọi (d) =d'. Khi đó d' song song hoặc trùng với d nên phương trình của nó có dạng x-2y+C=0. Lấy một điểm thuộc d chẳng hạn B(-1;1), khi đó
(B) = (-2;3) thuộc d' nên -2 -2.3 +C =0. Từ đó suy ra C = 8
Đúng 0
Bình luận (0)
Giải giúp mình với ạ
Tìm ảnh của đường tròn ( C ): x2 + y2 - 2x - 4 = 0 qua liên tiếp các phép biến hình sau:
phép vị tự V( O; -2 ), phép tịnh tiến T\(\overrightarrow{v}\) ( 1; -2 )
Bài 1: Trong mặt phẳng Oxy, cho đường thẳng d:2x-3y+40 và điểm A(3;-1).Tìm tọa độ vecto overrightarrow{v} có giá vuông góc với d biết phép tịnh tiến theo vecto overrightarrow{v} biến đường thẳng d thành đường thẳng Delta đi qua điểm A.Bài 2: Tính tổng các nghiệm thuộc khoảng left(0;2022piright) của phương trìnhleft(sinx+cosxright)^2+2sin^2dfrac{x}{2}sinxleft(2sqrt{3}sinx+4-sqrt{3}right)
Đọc tiếp
Bài 1: Trong mặt phẳng Oxy, cho đường thẳng \(d:2x-3y+4=0\) và điểm \(A(3;-1)\).Tìm tọa độ vecto \(\overrightarrow{v}\) có giá vuông góc với d biết phép tịnh tiến theo vecto \(\overrightarrow{v}\) biến đường thẳng d thành đường thẳng \(\Delta\) đi qua điểm A.
Bài 2: Tính tổng các nghiệm thuộc khoảng \(\left(0;2022\pi\right)\) của phương trình
\(\left(sinx+cosx\right)^2+2sin^2\dfrac{x}{2}=sinx\left(2\sqrt{3}sinx+4-\sqrt{3}\right)\)
Trong mặt phẳng Oxy, cho overrightarrow{v}left(2;0right) và điểm Mleft(1;1right)
a) Tìm tọa độ của điểm M là hình ảnh của điểm M qua phép dời hình có được bằng cách thực hiện liên tiếp phép đối xứng qua trục Oy và phép tịnh tiến theo vectơ overrightarrow{v}
b) Tìm tọa độ của điểm M là ảnh của điểm M qua phép dời hình có được bằng cách thực hiện liên tiếp phép tịnh tiến theo vectơ overrightarrow{v} và phép đối xứng qua trục Oy
Đọc tiếp
Trong mặt phẳng Oxy, cho \(\overrightarrow{v}\left(2;0\right)\) và điểm \(M\left(1;1\right)\)
a) Tìm tọa độ của điểm M' là hình ảnh của điểm M qua phép dời hình có được bằng cách thực hiện liên tiếp phép đối xứng qua trục Oy và phép tịnh tiến theo vectơ \(\overrightarrow{v}\)
b) Tìm tọa độ của điểm M" là ảnh của điểm M qua phép dời hình có được bằng cách thực hiện liên tiếp phép tịnh tiến theo vectơ \(\overrightarrow{v}\) và phép đối xứng qua trục Oy
a)
Qua phép đối xứng trục Oy điểm \(M\left(1;1\right)\) biến thành điểm \(M'\left(x;y\right)\) có tọa độ là: \(\left\{{}\begin{matrix}x'=-x=-1\\y'=y=1\end{matrix}\right.\).
Suy ra: \(M'\left(-1;1\right)\).
Qua phép tịnh tiến theo véc tơ \(\overrightarrow{v}\left(2;0\right)\) điểm M' biến thành điểm \(A\left(x_A;y_A\right)\) là:\(\left\{{}\begin{matrix}x_A=-1+2=1\\y_A=0+1=1\end{matrix}\right.\).
Suy ra: \(A\left(1;1\right)\equiv M\) là điểm cần tìm.
b) Gọi C là ảnh của điểm M qua phép tịnh tiến theo véc tơ \(\overrightarrow{v}\)
là: \(\left\{{}\begin{matrix}x_C=2+1=3\\y_C=0+1=1\end{matrix}\right.\). Suy ra: \(C\left(3;1\right)\)
\(M''=Đ_{Oy}\left(C\right)\) nên \(\left\{{}\begin{matrix}x_{M''}=-x_C=-3\\y_{M''}=y_C=1\end{matrix}\right.\). Suy ra: \(M''\left(-3;1\right)\).
Đúng 0
Bình luận (0)
1. Phép tịnh tiến theo vecto overrightarrow{v} biến đường thằng d: x+y0 thành d:x+y-40. Biết overrightarrow{v} cùng phương với vecto overrightarrow{u} (1;1). Tính độ dài vecto overrightarrow{v}
2. Cho 2 đường thẳng d:x+y-10 và d:x+y-50. Phép tịnh tiến theo vecto overrightarrow{u} biến đường thẳng d thành d. Khi đó độ dài nhỏ nhất của vecto overrightarrow{u}là bao nhiêu?
3. Cho 3 đường thẳng d:2x+y+30, d:2x+y-10. Có bao nhiêu vecto overrightarrow{v}có độ dàu bằng 2 sao cho phép tịnh tiến theo v...
Đọc tiếp
1. Phép tịnh tiến theo vecto \(\overrightarrow{v}\) biến đường thằng d: x+y=0 thành d':x+y-4=0. Biết \(\overrightarrow{v}\) cùng phương với vecto \(\overrightarrow{u}\) =(1;1). Tính độ dài vecto \(\overrightarrow{v}\)
2. Cho 2 đường thẳng d:x+y-1=0 và d':x+y-5=0. Phép tịnh tiến theo vecto \(\overrightarrow{u}\) biến đường thẳng d thành d'. Khi đó độ dài nhỏ nhất của vecto \(\overrightarrow{u}\)là bao nhiêu?
3. Cho 3 đường thẳng d:2x+y+3=0, d':2x+y-1=0. Có bao nhiêu vecto \(\overrightarrow{v}\)có độ dàu bằng 2 sao cho phép tịnh tiến theo vecto \(\overrightarrow{v}\)biến d thành d'
4. Cho 2 đường thẳng d; x+y+3=0, d':x+y+m=0. Biết có duy nhất một vecto \(\overrightarrow{v}\)có độ dài bằng \(\sqrt{2}\) sao cho phép tịnh tiến theo vecto \(\overrightarrow{v}\) biến d thành d'. Tìm m
1.
Do \(\overrightarrow{v}\) cùng phương với \(\overrightarrow{u}\) nên \(\overrightarrow{v}=\left(a;a\right)\) với a là số thực khác 0
Chọn \(M\left(0;0\right)\) là 1 điểm thuộc d
Gọi M' là ảnh của M qua phép tịnh tiến \(\overrightarrow{v}\Rightarrow M'\in d'\)
\(\left\{{}\begin{matrix}x_{M'}=a+0=a\\y_{M'}=a+0=a\end{matrix}\right.\) \(\Rightarrow M'\left(a;a\right)\)
Thay vào pt d' ta được:
\(a+a-4=0\Rightarrow a=2\)
\(\Rightarrow\overrightarrow{v}=\left(2;2\right)\)
\(\Rightarrow\left|\overrightarrow{v}\right|=2\sqrt{2}\)
2.
Gọi \(\overrightarrow{u}=\left(a;b\right)\)
Gọi \(A\left(0;1\right)\) là 1 điểm thuộc d
Gọi A' là ảnh của A qua phép tịnh tiến \(\overrightarrow{u}\Rightarrow A'\in d'\)
Ta có: \(\left\{{}\begin{matrix}x_{A'}=a\\y_{A'}=b+1\end{matrix}\right.\)
Thay tọa độ A' vào pt d' ta được: \(a+b+1-5=0\Leftrightarrow a+b=4\)
Ta có:
\(\left|\overrightarrow{u}\right|=\sqrt{a^2+b^2}\ge\sqrt{\frac{1}{2}\left(a+b\right)^2}=2\sqrt{2}\)
\(\Rightarrow\left|\overrightarrow{u}\right|_{min}=2\sqrt{2}\) khi \(a=b=2\)
3.
Gọi \(\overrightarrow{v}=\left(a;b\right)\Rightarrow a^2+b^2=4\) (1)
Gọi \(A\left(-1;-1\right)\) là 1 điểm thuộc d
Gọi A' là ảnh của A qua phép tịnh tiến \(\overrightarrow{v}\Rightarrow A'\in d'\)
Ta có: \(\left\{{}\begin{matrix}x_{A'}=-1+a\\x_{B'}=-1+b\end{matrix}\right.\)
Thay vào pt d':
\(2\left(a-1\right)+2\left(b-1\right)-1=0\)
\(\Leftrightarrow2a+2b=5\Rightarrow b=\frac{5-2a}{2}\)
Thế vào (1):
\(a^2+\left(\frac{5-2a}{2}\right)^2=4\)
\(\Leftrightarrow8a^2-20a+9=0\)
Pt trên có 2 nghiệm pb nên có 2 vecto thỏa mãn
Đúng 0
Bình luận (0)
Xem thêm câu trả lời