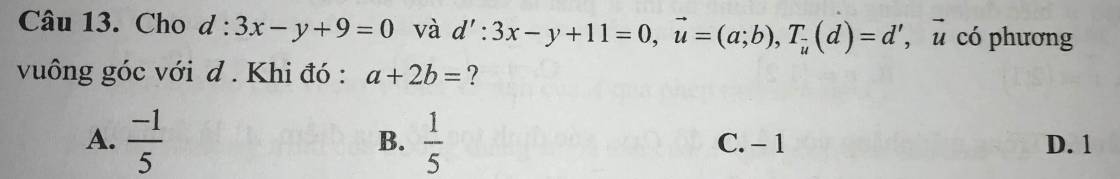Trong mp , cho điểm M(-3;2) , đường thẳng d:2y -3y+4=0 và vecto v=(-8;3). a) tìm ảnh của điểm M qua phép tịnh tiến theo vecto v=(-8;3). b) tìm phương trình đường thẳng d' là ảnh của d qua phép tịnh tiến theo vecto v=(-8;3).
Bài 2: Phép tịnh tiến
a: Tọa độ M' là:
x=-3-8=-11 và y=2+3=5
b: (d') là ảnh của (d) qua phép tịnh tiến \(\overrightarrow{v}=\left(-8;3\right)\)
=>(d')//(d)
=>(d'): 2x-3y+c=0
Lấy A(1;2) thuộc (d')
=>A'(-7;5)
Thay x=-7 và y=5 vào (d'), ta được:
c-14-15=0
=>c=29
Đúng 0
Bình luận (0)
Trong mặt phẳng oxy ,cho điềm M(-3;2) và vecto v=(-8;3) , đường thẳng d:2x-3y+4=0. a) tìm tọa độ M' là ảnh của M(-3;2) qua phép T vecto v. b) tìm phương trình đường thẳng d qua phép tịnh tiến theo vecto T.
1.Trong mặt phẳng Oxy,cho đường tròn (C) tâm I có phương trình \(x^2+y^2+6x-4y+4=0\)
Tìm tọa độ I' là ảnh của I qua phép tịnh tiến theo vecto \(\overrightarrow{v}\)(4;-3)
\(x^2+y^2+6x-4y+4=0\)
=>x^2+6x+9+y^2-4y+4-9=0
=>(x+3)^2+(y-2)^2=9
=>A(-3;2) và R=3
Tọa độ A' là:
\(\left\{{}\begin{matrix}x=-3+4=1\\y=2-3=-1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
toán 11 trong mặt phẳng oxy cho vectơ u = ( 3 ; 1 ) và đường thẳng denta x - 2y + 1 = 0 . phép tịnh tiến theo vectơ u biến denta thành đường thẳng denta phẩy . viết phương trình của denta phẩy
Lấy A(3;2) thuộc (delta)
=>A'(6;3)
Thay x=6và y=3 vào (delta'), ta được:
6-6+c=0
=>c=0
=>x-2y=0
Đúng 0
Bình luận (0)
Trong mp oxy cho ∆ABC có ảnh qua phép tịnh tiến theo vectơ v =(2,5) là ∆A'B'C' và ∆ A'B'C' có trọng tâm là G (-3,4) biết rằng A(-1,6);B(3,4).Tìm A',B',C'
Tọa độ A' là:
x=-1+2=1 và y=6+5=11
Tọa độ B' là:
x=3+2=5 và y=4+5=9
Theo đề, ta có:
\(\left\{{}\begin{matrix}-3=\dfrac{1+5+x_{C'}}{3}\\4=\dfrac{11+9+y_{C'}}{3}\end{matrix}\right.\Leftrightarrow C'\left(-15;-8\right)\)
Đúng 1
Bình luận (0)
Trong mặt phẳng tọa độ xOy, cho các điểm A', B' lần lượt là ảnh của các điểm A(2;3), B(1;1) qua phép tịnh tiến theo vectơ v(3;1). Tính độ dài vectơ A',B' A.2 B√3 C.√5 D√2
Lời giải:
Do $A', B'$ là ảnh của $A,B$ qua phép tịnh tiến vecto $\overrightarrow{v}=(3,1)$ nên:
\(|A'B'|=|AB|=\sqrt{(x_A-x_B)^2+(y_A-y_B)^2}=\sqrt{1^2+2^2}=\sqrt{5}\)
Đáp án C.
Đúng 1
Bình luận (0)
Bài 1: Cho 3 đường thẳng (1 đường tổng quát và 2 đường chứa tham số) và →vv→ (tự cho).T→vTv→.Bài 2: Cho 2 phương trình đường tròn (1 pt tổng quát và 1 pt chứa tổng quát) và →vv→ (tự cho). Xác định ảnh của đường tròn qua T3→vT3v→.mọi người giúp mk gấp với ạ, mai mk phải trả bài, m.n cứu mk vs
Đọc tiếp
Bài 1: Cho 3 đường thẳng (1 đường tổng quát và 2 đường chứa tham số) và (tự cho).
.
Bài 2: Cho 2 phương trình đường tròn (1 pt tổng quát và 1 pt chứa tổng quát) và (tự cho). Xác định ảnh của đường tròn qua .
mọi người giúp mk gấp với ạ, mai mk phải trả bài, m.n cứu mk vs
Bài 1: Cho 3 đường thẳng (1 đường tổng quát và 2 đường chứa tham số) và overrightarrow{v} (tự cho).a/ Xác định ảnh của 3 đường thẳng đó qua T_{overrightarrow{v}}.b/ Cho đường thẳng chứa tham số qua đường thẳng tổng quát.Bài 2: Cho 2 phương trình đường tròn (1 pt tổng quát và 1 pt chứa tổng quát) và overrightarrow{v} (tự cho). Xác định ảnh của đường tròn qua T_{3overrightarrow{v}}.mọi người giúp mk gấp với ạ. mấy cái trong ngoặc là m.n tự cho. mk ko bt cho lm s nên mong m.n giúp mk. cảm ơn ạ
Đọc tiếp
Bài 1: Cho 3 đường thẳng (1 đường tổng quát và 2 đường chứa tham số) và \(\overrightarrow{v}\) (tự cho).
a/ Xác định ảnh của 3 đường thẳng đó qua \(T_{\overrightarrow{v}}\).
b/ Cho đường thẳng chứa tham số qua đường thẳng tổng quát.
Bài 2: Cho 2 phương trình đường tròn (1 pt tổng quát và 1 pt chứa tổng quát) và \(\overrightarrow{v}\) (tự cho). Xác định ảnh của đường tròn qua \(T_{3\overrightarrow{v}}\).
mọi người giúp mk gấp với ạ. mấy cái trong ngoặc là m.n tự cho. mk ko bt cho lm s nên mong m.n giúp mk. cảm ơn ạ
`T_\vec{u} (d)=d'<=>d //// \vec{u}`
`->\bb A`
Đúng 2
Bình luận (0)
A. \(d\) song song với giá của \(\overrightarrow{u}\)
Đúng 0
Bình luận (0)