Trong mặt phẳng với hệ tọa độ oxy cho tam giác ABc có đỉnh B(2;-1) đường phân giác trong của góc a là đường thẳng đen ta có pt x+2y-5=0 điểm c thuộc trục tung sao cho khoảng cách từ điểm c đến đen ta =3 lần khoảng cách từ b đến đen ta tìm tọa độ c và viết pt các cạnh tam giác abc
ND
Những câu hỏi liên quan
Trong không gian với hệ tọa độ
O
x
y
z
, cho tam giác ABC có đỉnh
C
-
2
;
2
;
2
và trọng tâm
G
-
1
;
2
;
2
.
Tìm tọa độ các đỉnh A, B của tam giác ABC, biết A thuộc mặt...
Đọc tiếp
Trong không gian với hệ tọa độ O x y z , cho tam giác ABC có đỉnh C - 2 ; 2 ; 2 và trọng tâm G - 1 ; 2 ; 2 . Tìm tọa độ các đỉnh A, B của tam giác ABC, biết A thuộc mặt phẳng (Oxy) và điểm B thuộc trục cao.
A. A(-1;-1;0), B(0;0;4)
B. A(-1;1;0), B(0;0;4)
C. A(-1;0;1), B(0;0;4)
D. A(-4;4;0), B(0;0;1)
Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có trọng tâm G 2 3 ; 0 , biết M(1;1) là trung điểm cạnh BC. Tọa độ đỉnh A là:
A.(2;0)
B.(-2;0)
C.(0;-2)
D.(0;2)
Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có trọng tâm
G
(
2
3
;
0
)
, biết
M
(
1
;
1
)
là trung điểm cạnh BC. Tọa độ đỉnh A là: A. (2;0) B. (-2;0) C. (0;-2) D. (0;2)
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có trọng tâm G ( 2 3 ; 0 ) , biết M ( 1 ; 1 ) là trung điểm cạnh BC. Tọa độ đỉnh A là:
A. (2;0)
B. (-2;0)
C. (0;-2)
D. (0;2)
Trong mặt phẳng với hệ tọa độ oxy , cho tam giác ABC có đỉnh A(4-1) phương trình đường cao và trung tuyến kẻ từ đỉnh B lần lượt là 2x-3y+12=0 và 3 và 2x-3y=0. Xác định tọa độ các đỉnh còn lại của tam giác ABC
Bạn coi lại đề, 2 đường thẳng xuất phát từ B nhưng lại song song với nhau, điều này hoàn toàn vô lý
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có đỉnh A(2;1), trực tâm H(14;-7) đường trung tuyến kẻ từ đỉnh B có phương trình (d):
9x - 5y - 7=0. Tìm tọa độ các đỉnh B, C.
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(-2;4), B(4;1), C(-2;-1). Tìm tọa độ trực tâm H tam giác.
vecto AH=(x+2;y-4); vecto BC=(-6;-2)
vecto BH=(x-4;y-1); vecto AC=(0;-5)
Theo đề, ta có: -6(x+2)-2(y-4)=0 và 0(x-4)-5(y-1)=0
=>y=1 và -6(x+2)=2(y-4)=2*(1-4)=-6
=>x+2=1 và y=1
=>x=-1 và y=1
Đúng 1
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có các đỉnh A(-1;0); B(4;0);C(0;m).
Tìm tọa độ trọng tâm G của tam giác ABC theo m. Tìm m để tam giác GAB vuông tại G
Gọi \(\left(x_G;y_G\right)\) là tọa độ của G. Theo công thức tính trọng tâm tam giác, ta có :
\(\begin{cases}x_G=\frac{-1+4+0}{3}=1\\y_G=\frac{0+0+m}{3}=\frac{m}{3}\end{cases}\)
Vậy \(G\left(1;\frac{m}{3}\right)\)
\(\widehat{AGB}=90^0\Leftrightarrow\overrightarrow{BG}\perp AG\Leftrightarrow\overrightarrow{BG}.\overrightarrow{AG}=0\) (1)
\(\overrightarrow{BG}=\left(1-4;\frac{m}{3}-0\right)=\left(-3;\frac{m}{3}\right)\)
\(\overrightarrow{AG}=\left(1+1;\frac{m}{3}-0\right)=\left(2;\frac{m}{3}\right)\)
\(\overrightarrow{BG}.\overrightarrow{AG}=\frac{m^2}{9}-6\) (2)
Thay (2) vào (1) ta có : \(\widehat{AGB}=90^0\Leftrightarrow m^2=54\Leftrightarrow m=\pm3\sqrt{6}\)
Vậy có 2 giá trị cần tìm của m
Đúng 0
Bình luận (0)
1.Trong mặt phẳng tọa độ Oxy cho hình bình hành ABCD với A (- 6;1); B (2;2) C (1;5) tọa độ đỉnh D là:
A. (5;2)
B. (-7;4)
C. (5;4)
D. (7;-4)
2.Trong mặt phẳng tọa độ Oxy cho tam giác ABC với A (- 1;3); B (2;1) C (5;5) tọa độ đỉnh D là của hình bình hành ABCD:
A. (0;4)
B. (8;1)
C. (8;3)
D. (-8;3)
Hướng dẫn em cách làm với ạ. Em cảm ơn nhiều.
1, Gọi tọa độ điểm D(x;y)
Ta có:\(\overrightarrow{AB}\left(8;1\right)\)
\(\overrightarrow{DC}\left(1-x;5-y\right)\)
Tứ giác ABCD là hình bình hành khi
\(\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Leftrightarrow1-x=8;5-y=1\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-7\\y=4\end{matrix}\right.\)
Vậy tọa độ điểm D(-7;4)
Đúng 1
Bình luận (1)
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có trực tâm H(-1;3), tâm đường tròn ngoại tiếp I(-3;3), chân đường cao kẻ từ đỉnh A là điểm K(-1;1). Tìm tọa độ các đỉnh A, B, C
Ta có \(HK\perp BC,K\in BC;\overrightarrow{HK}=\left(0;-2\right)\Rightarrow y-1=0\)
Gọi M là trung điểm của BC ta có phương trình \(x+3=0;M=IM\cap BC\Rightarrow M\left(-3;1\right)\)
Gọi D là điểm đối xứng của A qua I chỉ ra BHCD là hình bình hành. Khi đó M là trung điểm của HD, suy ra D(-5;-1).
I là trung điểm của AD, suy ra A(-1;7)
\(AI=\sqrt{20}\), phương trình đường tròn ngoại tiếp tam giác ABC là : \(\left(x+3\right)^2+\left(y-3\right)^2=20\)
Tọa độ điểm B, C là nghiệm của hệ phương trình :
\(\begin{cases}y-1=0\\\left(x+3\right)^2+\left(y-3\right)^2=20\end{cases}\)\(\Leftrightarrow\begin{cases}x=1\\y=1\end{cases}\) hoặc \(\begin{cases}x=-7\\y=1\end{cases}\)
Vậy ta có \(B\left(1;1\right),C\left(-7;1\right)\) hoặc \(B\left(-7;1\right),C\left(1;1\right)\)
Suy ra \(A\left(-1;7\right);B\left(1;1\right),C\left(-7;1\right)\)
hoặc\(A\left(-1;7\right);B\left(-7;1\right),C\left(1;1\right)\)
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ tọa độ (Oxy), cho tam giác ABC có đỉnh B(-12;1) đường phân giác của góc A có phương trình d:x+2y-50.
G
1
3
;
2
3
là trọng tâm tam giác ABC. Đường thẳng BC đi qua điểm nào sau đây A. (1;0) B. (2;-3) C. (4;-4) D. (4;3)
Đọc tiếp
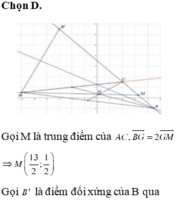
Trong mặt phẳng với hệ tọa độ (Oxy), cho tam giác ABC có đỉnh B(-12;1) đường phân giác của góc A có phương trình d:x+2y-5=0. G 1 3 ; 2 3 là trọng tâm tam giác ABC. Đường thẳng BC đi qua điểm nào sau đây
A. (1;0)
B. (2;-3)
C. (4;-4)
D. (4;3)