Cho ΔABC=ΔPQRΔABC=ΔPQR biết AB = 6cm; BC = 7cm. Chu vi tam giác ABC là 18cm. Độ dài cạnh PR là:
H24
Những câu hỏi liên quan
Cho điểm O nằm trong ΔABC. Gọi P, Q, R lần lượt là trung điểm của các đoạn thẳng OA, OB, OC.
a. Chứng minh: ΔPQR đồng dạng ΔABC b. Tính chu vi ΔPQR, biết chu vi ΔABC bằng 540 cm.
a. Xét △OAB có:
Q là trung điểm OB, P là trung điểm OA (gt).
\(\Rightarrow\) PQ là đường trung bình của △OAB.
\(\Rightarrow PQ=\dfrac{1}{2}AB\)
\(\Rightarrow\dfrac{PQ}{AB}=\dfrac{\dfrac{1}{2}AB}{AB}=\dfrac{1}{2}\)
-Tương tự: \(\dfrac{QR}{BC}=\dfrac{1}{2};\dfrac{PR}{AC}=\dfrac{1}{2}\)
-Xét △PQR và △ABC có:
\(\dfrac{PQ}{AB}=\dfrac{QR}{BC}=\dfrac{PR}{AC}\left(=\dfrac{1}{2}\right)\)
\(\Rightarrow\)△PQR ∼ △ABC (c-c-c).
b. Ta có: △PQR ∼ △ABC (cmt).
\(\Rightarrow\dfrac{S_{PQR}}{S_{ABC}}=\left(\dfrac{PQ}{AB}\right)^2=\left(\dfrac{1}{2}\right)^2=\dfrac{1}{4}\)
\(\Rightarrow S_{PQR}=\dfrac{1}{2}S_{ABC}=\dfrac{1}{2}.540=270\left(cm^2\right)\)
Đúng 1
Bình luận (1)
Cho tam giác ABC và một điểm O nằm trong tam giác đó. Gọi P, Q, R lần lượt là trung điểm của các đoạn thẳng OA, OB, OC.a) Chứng minh
Δ
P
Q
R
∽
Δ
A
B
C
.b) Cho biết
Δ
A
B
C
có chu vi bằng 543cm, hãy tính chu vi
Δ
P
Q
R
.
Đọc tiếp
Cho tam giác ABC và một điểm O nằm trong tam giác đó. Gọi P, Q, R lần lượt là trung điểm của các đoạn thẳng OA, OB, OC.
a) Chứng minh Δ P Q R ∽ Δ A B C .
b) Cho biết Δ A B C có chu vi bằng 543cm, hãy tính chu vi Δ P Q R .
cho ΔABC = ΔPQR. biết A= 50 độ và B-C = 50 độ.
a, chứng minh rằng ΔPQR là tam giác vuông
b, chỉ ra các cặp cạnh bằng nhau của mỗi tam giác
a,
\(\Delta ABC=\Delta PQR\\ \Rightarrow\widehat{A}=\widehat{P}=50^o\\ \widehat{B}=\widehat{Q}\)
Xét \(ABC\) có
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow\widehat{B}+\widehat{C}=130^o\\ \Rightarrow\widehat{B}=130^o-\widehat{C}\)
\(\widehat{B}-\widehat{C}=50^o\\ \Rightarrow130^o-2\widehat{C}=50^o\\ \Rightarrow\widehat{C}-40^o\\ \Rightarrow\widehat{B}=90^o=\widehat{Q}\)
\(\Rightarrow PQR\) là tam giác vuông
b, \(\Delta ABC=\Delta PQR\\ \Rightarrow\left\{{}\begin{matrix}AC=PR\\AB=PQ\\BC=QR\end{matrix}\right.\)
Đúng 2
Bình luận (0)
1.
a) Cho ΔABC có : AC=5cm, BC=3cm. Tìm cạnh AB biết, AB là số nguyên và AB>6cm
b) Cho ΔABC có: AB=8cm, AC=6cm. Tính BC, biết BC là số nguyên BC<4cm
a: AC-BC<AB<AC+BC
=>5<AB<8
mà AB>6
nên AB=7cm
b: AB-AC<BC<AB+AC
=>2<BC<14
mà BC<4
nên BC=3cm
Đúng 1
Bình luận (0)
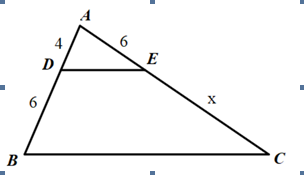
Cho hình vẽ, biết ΔABC có DE=BC , AB = 4cm , DB = 6cm AE = 6cm . Tìm x
\(DE=EC\\ \Rightarrow DE//BC\\ \Rightarrow\dfrac{AD}{DB}=\dfrac{AE}{EC}\Rightarrow\dfrac{4}{6}=\dfrac{6}{x}\\ \Rightarrow x=9\)
Đúng 1
Bình luận (3)
Cho ΔABC đồng dạng với ΔMNP. Biết AB = 2cm, BC = 3cm, MN = 6cm, MP = 6cm. Hãy chọn khẳng định sai:
A. AC = 2cm
B. NP = 9cm
C. ΔMNP cân tại M
D. ΔABC cân tại C
Vì ΔABC đồng dạng với ΔMNP nên A B M N = A C M P = B C N P hay 2 6 = A C 6 = 3 N P
=> AC = 2.6 6 = 2; NP = 6.3 2 = 9
Vậy NP = 9cm, AC = 2cm nên A, B đúng.
Tam giác ABC cân tại A, MNP cân tại M nên C đúng, D sai.
Đáp án: D
Đúng 0
Bình luận (0)
Cho ΔDEF ∼ ΔABC biết DE = 5cm, AB = 6cm, AC = 12cm. Độ dài DF là:
A. 8cm
B. 9cm
C. 10cm
D. 15cm
Cho ΔABC vuông tại A. Tính AB biết HB = 2cm; HC=8cm, AC=6cm
Anh bổ sung là : AH vuông góc với BC nhé
\(BC=HB+HC=2+8=10\left(cm\right)\)
\(\text{Áp dụng định lý Pytago trong tam giác ABC vuông tại A:}\)
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AB=\sqrt{BC^2-AC^2}=\sqrt{10^2-6^2}=8\left(cm\right)\)
Đúng 1
Bình luận (0)
Bổ sung đề \(AH\) là đường cao.
Áp dụng hệ thức lượng vào tam giác vuông \(ABC\) và đường cao \(AH\) ta có :
\(AB^2=BC.BH\)
\(\Rightarrow AB=\sqrt{BC.BH}=\sqrt{\left(8+2\right).2}=\sqrt{20}=2\sqrt{5}\)\((cm)\)
Đúng 1
Bình luận (0)
Đề bài sai rồi em
Nếu H là chân đường cao trên BC thì tam giác HAC vuông tại H
Khi đó trong tam giác vuông HAC có AC là cạnh huyền và CH là cạnh góc vuông
Nhưng CH=8>AC=6 là hoàn toàn vô lý
Đúng 1
Bình luận (0)
Bài1:Cho ΔMNP vuông tại N. Tính độ dài MN biết MP√30cm,NP√14 cmBài2:Cho ΔABC cân tại A. Biết AB2cm. Tính BCBài3:Cho ΔABC vuông tại A,AH⊥BC tại H. Tính độ dài các cạnh của ΔABC biết AH6cm,HB4cm,HC9cmBài4:Cho ΔABC vuông tại A,AH⊥BC tại H. Tính độ dài các cạnh của ΔABC biết AH4cm,HB2cm,HC8cmBài5:Cho ΔABC vuông tại A,AH⊥BC tại H.Biết AB4cm,HB2cm,HC8cm.Tính BC,AH,ACBài6:Cho ΔABC vuông tại A,AH⊥BC tại H.Biết AB6cm,AC8cm và dfrac{HB}{HC}dfrac{9}{16}Tính HB,HC
Đọc tiếp
Bài1:Cho ΔMNP vuông tại N. Tính độ dài MN biết MP=√30cm,NP=√14 cm
Bài2:Cho ΔABC cân tại A. Biết AB=2cm. Tính BC
Bài3:Cho ΔABC vuông tại A,AH⊥BC tại H. Tính độ dài các cạnh của ΔABC biết AH=6cm,HB=4cm,HC=9cm
Bài4:Cho ΔABC vuông tại A,AH⊥BC tại H. Tính độ dài các cạnh của ΔABC biết AH=4cm,HB=2cm,HC=8cm
Bài5:Cho ΔABC vuông tại A,AH⊥BC tại H.Biết AB=4cm,HB=2cm,HC=8cm.Tính BC,AH,AC
Bài6:Cho ΔABC vuông tại A,AH⊥BC tại H.Biết AB=6cm,AC=8cm và \(\dfrac{HB}{HC}\)=\(\dfrac{9}{16}\)Tính HB,HC
Bài 3:
\(AB=\sqrt{AH^2+BH^2}=\sqrt{6^2+4^2}=2\sqrt{13}\left(cm\right)\)
BC=13cm
=>\(AC=3\sqrt{13}\left(cm\right)\)
Đúng 0
Bình luận (0)








