Tập xác định của hàm số \(y=\left(3^x-9\right)^{-2}\) là:
A. \(D=R\)
B. \(D=R\backslash\left\{2\right\}\)
C. \(D=\left(-\infty;2\right)\)
D. \(D=\left(2;+\infty\right)\)
Lời giải:
ĐKXĐ: $3^x-9\neq 0\Lefrightarrow 3^x\neq 9\Leftrightarrow x\neq 2$
Đáp án B.
Đúng 3
Bình luận (4)
Tìm tập xác định của hàm số \(y = \frac{1}{{\sqrt {x - 2} }}\) là:
A. \(D = \left[ {2; + \infty } \right).\)
B. \(D = \left( {2; + \infty } \right).\)
C. \(D = \mathbb{R}\backslash \left\{ 2 \right\}.\)
D. \(D = \mathbb{R}.\)
Để hàm số \(y = \frac{1}{{\sqrt {x - 2} }}\) xác định \( \Leftrightarrow \,\,x - 2 > 0\,\, \Leftrightarrow \,\,x > 2.\)
Vậy tập xác định của hàm số là: \(D = \left( {2; + \infty } \right).\)
Chọn B.
Đúng 0
Bình luận (0)
Cho hàm số yf(x) xác định trên (a;b). Nếu forallleft(x_oright),x_nne x_o,ltext{imx}_nx_oRightarrow ltext{imf}left(x_nright)+infty thì:A. limlimits_{x-x_o}fleft(xright)LB. limlimits_{x-x_o^-}fleft(xright)-inftyC. limlimits_{x-x_o}fleft(xright)-inftyD. limlimits_{x-x_o}fleft(xright)+infty
Đọc tiếp
Cho hàm số y=f(x) xác định trên (a;b). Nếu \(\forall\left(x_o\right),x_n\ne x_o,l\text{imx}_n=x_o\Rightarrow l\text{imf}\left(x_n\right)=+\infty\) thì:
A. \(\lim\limits_{x->x_o}f\left(x\right)=L\)
B. \(\lim\limits_{x->x_o^-}f\left(x\right)=-\infty\)
C. \(\lim\limits_{x->x_o}f\left(x\right)=-\infty\)
D. \(\lim\limits_{x->x_o}f\left(x\right)=+\infty\)
\(\lim\limits_{x\rightarrow x_0}f\left(x\right)=+\infty\)
Đúng 0
Bình luận (0)
Xác định một hàm số \(y=f\left(x\right)\) thỏa mãn đồng thời các điều kiện sau :
a) \(f\left(x\right)\) xác định trên R\{1}
b) \(\lim\limits_{x\rightarrow1}f\left(x\right)=+\infty;\lim\limits_{x\rightarrow+\infty}f\left(x\right)=2;\lim\limits_{x\rightarrow-\infty}f\left(x\right)=2\)
thì f(x) thỏa mãn được tất cả các điều kiện đã nêu
Đúng 0
Bình luận (0)
PD
2 tháng 10 2021 lúc 21:47
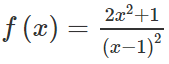
cho hàm số y = f(x) xác định và f(x) \(\ne0\) \(\forall x\in\left(0;+\infty\right)\), \(f'\left(x\right)=\left(2x+1\right)f^2\left(x\right)\) và f(1) = -1/2. Biết tổng f(1) + f(2) + f(3) + ... + f(2017) = a/b (a,b\(\in R\)) với a/b tối giản. Tìm a,b
Cho hai hàm số yfleft(xright) và ygleft(xright) cùng xác định trên khoảng left(-infty;aright). Dùng định nghĩa chứng minh rằng nếu limlimits_{xrightarrow-infty}fleft(xright)L và limlimits_{xrightarrow-infty}gleft(xright)M thì limlimits_{xrightarrow-infty}fleft(xright).gleft(xright)L.M
Đọc tiếp
Cho hai hàm số \(y=f\left(x\right)\) và \(y=g\left(x\right)\) cùng xác định trên khoảng \(\left(-\infty;a\right)\). Dùng định nghĩa chứng minh rằng nếu \(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=L\) và \(\lim\limits_{x\rightarrow-\infty}g\left(x\right)=M\) thì \(\lim\limits_{x\rightarrow-\infty}f\left(x\right).g\left(x\right)=L.M\)
Cho hàm số bậc hai y f(x) {x^2} - 4x + 3a) Xác định hệ số a. Tính f(0);f(1);f(2);f(3);f(4) và nhận xét về dấu của chúng so với dấu của hệ số ab) Cho đồ thị hàm số yf(x) (H.6.17). Xét từng khoảng left( { - infty ;1} right);left( {1;3} right);left( {3; + infty } right), đồ thị nằm phía trên hay phía dưới trục Ox?c) Nhận xét về dấu của f(x) và dấu của hệ số a trên từng khoảng đó.
Đọc tiếp
Cho hàm số bậc hai \(y = f(x) = {x^2} - 4x + 3\)
a) Xác định hệ số a. Tính \(f(0);f(1);f(2);f(3);f(4)\) và nhận xét về dấu của chúng so với dấu của hệ số a
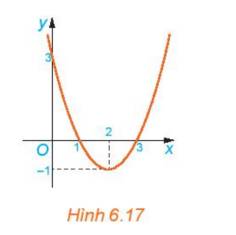
b) Cho đồ thị hàm số y=f(x) (H.6.17). Xét từng khoảng \(\left( { - \infty ;1} \right);\left( {1;3} \right);\left( {3; + \infty } \right)\), đồ thị nằm phía trên hay phía dưới trục Ox?
c) Nhận xét về dấu của f(x) và dấu của hệ số a trên từng khoảng đó.
a) Hệ số a là: a=1
\(f(0) = {0^2} - 4.0 + 3 = 3\)
\(f(1) = {1^2} - 4.1 + 3 = 0\)
\(f(2) = {2^2} - 4.2 + 3 = - 1\)
\(f(3) = {3^2} - 4.3 + 3 = 0\)
\(f(4) = {4^2} - 4.4 + 3 = 3\)
=> f(0); f(4) cùng dấu với hệ số a; f(2) khác dấu với hệ số a
b) Nhìn vào đồ thị ta thấy
- Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành
- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành
- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành
c) - Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành => f(x)>0, cùng dầu với hệ số a
- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành => f(x) <0, khác dấu với hệ số a
- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành => f(x)>0, cùng dấu với hệ số a
Đúng 0
Bình luận (0)
H24
SGK Chân trời sáng tạo
20 tháng 8 2023 lúc 19:17
a) Xét hàm số y {log _2}x với tập xác định D left( {0; + infty } right).i) Hoàn thành bảng giá trị sau:ii) Trong mặt phẳng toạ độ Oxy, xác định các điểm có toạ độ như bảng trên. Làm tương tự, lấy nhiều điểm Mleft( {x;{{log }_2}x} right) với x 0 và nối lại ta được đồ thị hàm số y {log _2}x như Hình 4. Từ đồ thị này, nêu nhận xét về tính liên tục, tính đồng biến, nghịch biến, giới hạn khi x to + infty ,x to {0^ + } và tập giá trị của hàm số đã cho.b) Lập bảng giá trị và vẽ đồ thị của hàm số y...
Đọc tiếp
a) Xét hàm số \(y = {\log _2}x\) với tập xác định \(D = \left( {0; + \infty } \right)\).
i) Hoàn thành bảng giá trị sau:
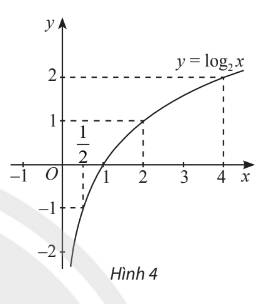
ii) Trong mặt phẳng toạ độ \(Oxy\), xác định các điểm có toạ độ như bảng trên. Làm tương tự, lấy nhiều điểm \(M\left( {x;{{\log }_2}x} \right)\) với \(x > 0\) và nối lại ta được đồ thị hàm số \(y = {\log _2}x\) như Hình 4. Từ đồ thị này, nêu nhận xét về tính liên tục, tính đồng biến, nghịch biến, giới hạn khi \(x \to + \infty ,x \to {0^ + }\) và tập giá trị của hàm số đã cho.
b) Lập bảng giá trị và vẽ đồ thị của hàm số \(y = {\log _{\frac{1}{2}}}x\). Từ đó, nhận xét về tính liên tục, tính đồng biến, nghịch biến, giới hạn khi \(x \to + \infty ,x \to {0^ + }\) và tập giá trị của hàm số này.
a:
i:
| x | 1/2 | 1 | 2 | 4 |
| y | -1 | 0 | 1 | 2 |
ii:
Hàm số liên tục và đồng biến trên \(\left(0;+\infty\right)\)
\(\lim\limits_{x\rightarrow+\infty}log_2x=+\infty;\lim\limits_{x\rightarrow0^+}log_2x=-\infty\)
Tập giá trị: R
b:
| x | 1/2 | 1 | 2 | 4 |
| y | 1 | 0 | -1 | -2 |
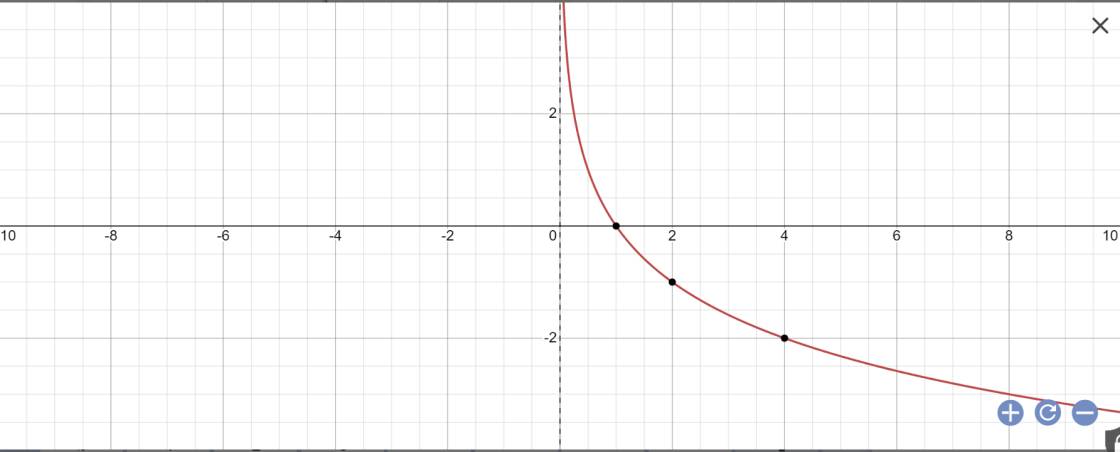
Hàm số liên tục và nghịch biến trên \(\left(0;+\infty\right)\)
\(\lim\limits_{x\rightarrow+\infty}log_{\dfrac{1}{2}}x=-\infty;\lim\limits_{x\rightarrow0^+}log_{\dfrac{1}{2}}x=+\infty\)
Tập giá trị: R
Đúng 0
Bình luận (0)
Biết rằng hàm số \(y = 2{x^2}{\rm{ + }}mx + n\) giảm trên khoảng \(\left( { - \infty ;1} \right),\)tăng trên khoảng \(\left( {1; + \infty } \right)\) và có tập giá trị là \([9; + \infty )\). Xác định giá trị của m và n.
Tham khảo:
Đỉnh S có tọa độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - m}}{{2.2}} = - \frac{m}{4};{y_S} = f( - \frac{m}{4})\)
Vì hàm số bậc hai có \(a = 2 > 0\) nên ta có bảng biến thiên sau:
Hàm số đạt giá trị nhỏ nhất bằng \(f( - \frac{m}{4}).\)
Hàm số giảm trên \(( - \infty ; - \frac{m}{4})\) và tăng trên \(( - \frac{m}{4}; + \infty )\)
Theo giả thiết, ta có:
Hàm số giảm trên khoảng \(\left( { - \infty ;1} \right)\)\( \Rightarrow \left( { - \infty ;1} \right) \subset ( - \infty ; - \frac{m}{4}) \Leftrightarrow 1 \le - \frac{m}{4}.\)
Tương tự hàm số tăng trên khoảng \(\left( {1; + \infty } \right)\)\( \Rightarrow \left( {1; + \infty } \right) \subset ( - \frac{m}{4}; + \infty ) \Leftrightarrow - \frac{m}{4} \le 1.\)
Do đó: \( - \frac{m}{4} = 1\) hay \(m = - 4\)
Lại có: Tập giá trị là \([9; + \infty )\)\( \Rightarrow \)Giá trị nhỏ nhất của hàm số bằng 9.
\( \Leftrightarrow f(1) = f( - \frac{m}{4}) = 9 \Leftrightarrow {2.1^2} + ( - 4).1 + n = 9 \Leftrightarrow n = 11.\)
Vậy \(m = - 4,n = 11.\)
Đúng 0
Bình luận (0)
Cho hai hàm số fleft( x right) {x^2} và gleft( x right) {x^3}, với các đồ thị như hình dưới đây.a) Tìm các tập xác định {D_f},;{D_g} của các hàm số fleft( x right) và gleft( x right).b) Chứng tỏ rằng fleft( { - x} right) fleft( x right),;forall x in {D_f}. Có nhận xét gì về tính đối xứng của đồ thị hàm số y fleft( x right) đối với hệ trục tọa độ Oxy?c) Chứng tỏ rằng gleft( { - x} right) - gleft( x right),;forall x in {D_g}. Có nhận xét gì về tính đối xứng của đồ thị hàm số y gleft( x righ...
Đọc tiếp
Cho hai hàm số \(f\left( x \right) = {x^2}\) và \(g\left( x \right) = {x^3}\), với các đồ thị như hình dưới đây.
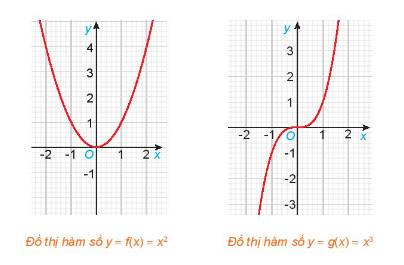
a) Tìm các tập xác định \({D_f},\;{D_g}\) của các hàm số \(f\left( x \right)\) và \(g\left( x \right)\).
b) Chứng tỏ rằng \(f\left( { - x} \right) = f\left( x \right),\;\forall x \in {D_f}\). Có nhận xét gì về tính đối xứng của đồ thị hàm số \(y = f\left( x \right)\) đối với hệ trục tọa độ Oxy?
c) Chứng tỏ rằng \(g\left( { - x} \right) = - g\left( x \right),\;\forall x \in {D_g}\). Có nhận xét gì về tính đối xứng của đồ thị hàm số \(y = g\left( x \right)\) đối với hệ trục tọa độ Oxy?
a) Tập xác định của hàm số đã cho là: \({D_f} = \mathbb{R};\;{D_g} = \mathbb{R}\)
b) Ta có: \(f\left( { - x} \right) = {\left( { - x} \right)^2} = {x^2} = f\left( x \right)\)
Đồ thị của hàm số \(y = f\left( x \right) = {x^2}\) đối xứng qua trục tung
c) Ta có: \(g\left( { - x} \right) = {\left( { - x} \right)^3} = - {x^3} = - g\left( x \right)\)
Đồ thị của hàm số \(y = g\left( x \right) = {x^3}\) đối xứng qua gốc tọa độ
Đúng 0
Bình luận (0)