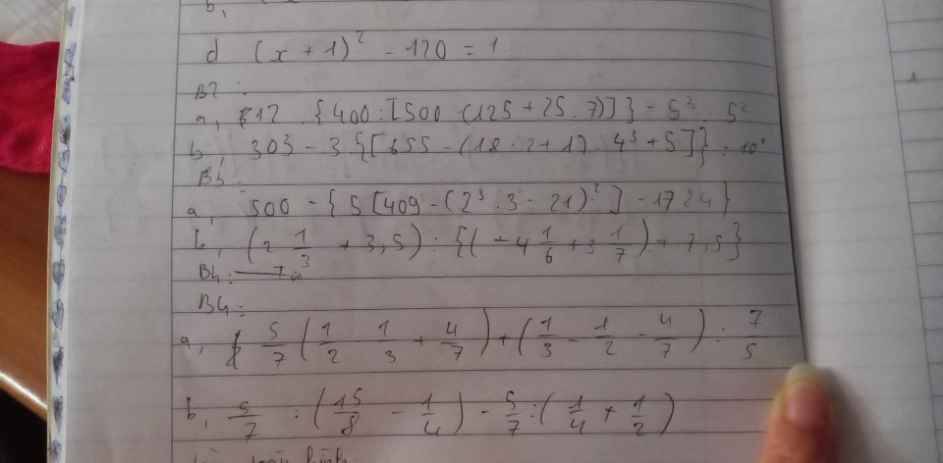Ôn tập chương 1

a: Xét ΔBMD vuông tại D và ΔCME vuông tại E có

MB=MC

\(\widehat{BMD}=\widehat{CME}\)(hai góc đối đỉnh)

Do đó: ΔBMD=ΔCME

=>BD=CE

Ta có: BD\(\perp\)AM

CE\(\perp\)AM

Do đó: BD//CE

b: Xét tứ giác BDCE có

BD//CE

BD=CE

Do đó: BDCE là hình bình hành

=>BE//CD và BE=CD

c: \(AD+AE=AD+AD+DE\)

\(=2AD+2DM\)

\(=2\left(AD+DM\right)=2AM\)

5/6 x + 3).2 = 4/9

5/6 x + 3 = 4/9 : 2

5/6 x + 3 = 2/9

5/6 x = 2/9 - 3

5/6 x = -7/9

x = -7/9 : 5/6

x = -14/15

Lời giải:

Gọi số mét vải 3 loại người đó mua lần lượt là $a,b,c$ 

Ta có:
$a+b+c=5,7$

$0,7a=0,8b=1,4c$
$\Rightarrow \frac{a}{\frac{10}{7}}=\frac{b}{\frac{10}{8}}=\frac{c}{\frac{10}{14}}$

Áp dụng TCDTSBN:

$\frac{a}{\frac{10}{7}}=\frac{b}{\frac{10}{8}}=\frac{c}{\frac{10}{14}}=\frac{a+b+c}{\frac{10}{7}+\frac{10}{8}+\frac{10}{14}}$
$=\frac{5,7}{\frac{95}{28}}=1,68$

$\Rightarrow a=1,68.\frac{10}{7}=2,4$ (m); $b=1,68.\frac{10}{8}=2,1$ (m); $c=1,68.\frac{10}{14}=1,2$ (m)

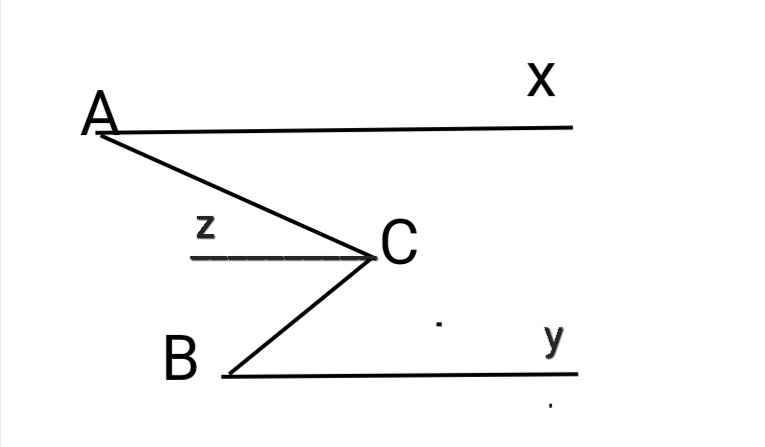
Sửa đề: Tính số đo ∠ACB

Giải

Vẽ tia Cz // Ax // By

Do Ax // Cz

⇒ ∠ACz = ∠xAC (so le trong)

Do Cz // By

⇒ ∠zCB = ∠yBC  (so le trong)

⇒ ∠ACB = ∠ACz + ∠zCB

= ∠xAC + ∠yBC

= 90⁰

Bài 4:

a: \(\dfrac{5}{7}\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{4}{7}\right)+\left(\dfrac{1}{3}-\dfrac{1}{2}-\dfrac{4}{7}\right):\dfrac{7}{5}\)

\(=\dfrac{5}{7}\cdot\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{4}{7}\right)+\dfrac{5}{7}\left(\dfrac{1}{3}-\dfrac{1}{2}-\dfrac{4}{7}\right)\)

\(=\dfrac{5}{7}\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{4}{7}+\dfrac{1}{3}-\dfrac{1}{2}-\dfrac{4}{7}\right)\)

\(=\dfrac{5}{7}\cdot0=0\)

b: \(\dfrac{5}{7}:\left(\dfrac{15}{8}-\dfrac{1}{4}\right)-\dfrac{5}{7}:\left(\dfrac{1}{4}+\dfrac{1}{2}\right)\)

\(=\dfrac{5}{7}:\dfrac{15-2}{8}-\dfrac{5}{7}:\dfrac{1+2}{4}\)

\(=\dfrac{5}{7}\cdot\dfrac{8}{13}-\dfrac{5}{7}\cdot\dfrac{4}{3}\)

\(=\dfrac{5}{7}\left(\dfrac{8}{13}-\dfrac{4}{3}\right)=\dfrac{5}{7}\cdot\dfrac{24-52}{39}\)

\(=\dfrac{5}{7}\cdot\dfrac{-28}{39}=\dfrac{-28}{7}\cdot\dfrac{5}{39}=-\dfrac{20}{39}\)

Bài 1

d: \(\left(x+1\right)^2-120=1\)

=>\(\left(x+1\right)^2=121\)

=>\(\left[{}\begin{matrix}x+1=11\\x+1=-11\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=10\\x=-12\end{matrix}\right.\)

Bài 7:

Xét ΔABC có \(\widehat{B}=\widehat{C}\)

nên ΔABC cân tại A

ΔABC cân tại A

mà AH là đường cao

nên AH là phân giác của \(\widehat{BAC}\)

Bài 9:

Xét ΔBAD vuông tại A và ΔBCE vuông tại C có

\(\widehat{ABD}=\widehat{CBE}\)

Do đó: ΔBAD\(\sim\)ΔBCE

=>\(\widehat{BDA}=\widehat{BEC}\)

=>\(\widehat{BDA}=\widehat{CED}\)

mà \(\widehat{BDA}=\widehat{CDE}\)

nên \(\widehat{CED}=\widehat{CDE}\)

=>ΔCDE có hai góc bằng nhau

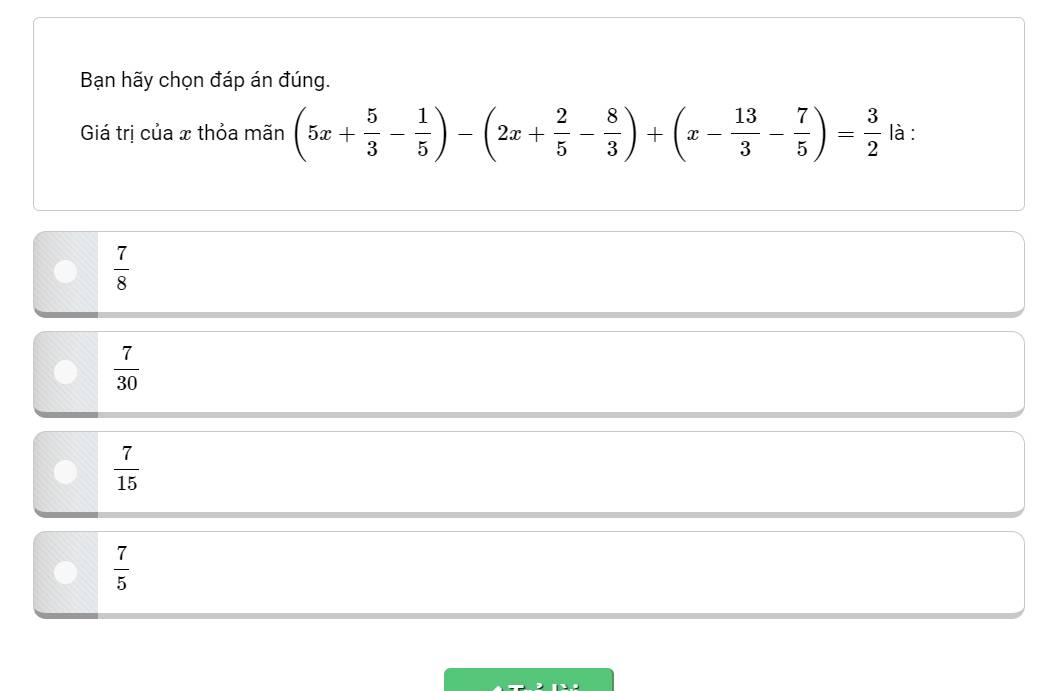
\(\left(5x+\dfrac{5}{3}-\dfrac{1}{5}\right)-\left(2x+\dfrac{2}{5}-\dfrac{8}{3}\right)+\left(x-\dfrac{13}{3}-\dfrac{7}{5}\right)=\dfrac{3}{2}\)

\(\Rightarrow5x+\dfrac{5}{3}-\dfrac{1}{5}-2x-\dfrac{2}{5}+\dfrac{8}{3}+x-\dfrac{13}{3}-\dfrac{7}{5}=\dfrac{3}{2}\)

\(\Rightarrow\left(5x-2x+x\right)+\left(\dfrac{5}{3}+\dfrac{8}{3}-\dfrac{13}{3}\right)+\left(-\dfrac{1}{5}-\dfrac{2}{5}-\dfrac{7}{5}\right)=\dfrac{3}{2}\)

\(\Rightarrow4x+0-\dfrac{10}{5}=\dfrac{3}{2}\)

\(\Rightarrow4x-2=\dfrac{3}{2}\)

\(\Rightarrow4x=\dfrac{3}{2}+2\)

\(\Rightarrow4x=\dfrac{7}{2}\)

\(\Rightarrow x=\dfrac{7}{2}:4\)

\(\Rightarrow x=\dfrac{7}{8}\) 

⇒ Chọn phương án đầu tiên 

Diện tích mảnh sân là:

\(12\cdot6=72\left(m^2\right)\)

Diện tích 1 viên gạch là:

\(60^2=3600\left(cm^2\right)=0,36\left(m^2\right)\)

Số viên gạch cần dùng là:

\(\dfrac{72}{0,36}=200\left(viên\right)\)

Khối lượng của 3 thùng hàng là:

1.2*3=3,6(tấn)

Tổng khối lượng xe và hàng là:

12+3,6=15,6(tấn)

-1/3