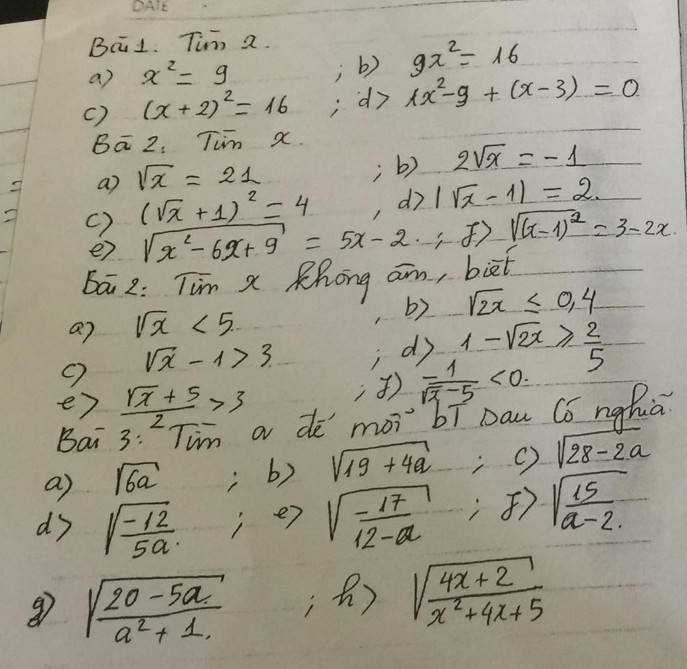Bài 1:
a: \(x^2=9\)
=>\(x^2=3^2=\left(-3\right)^2\)
=>\(x=\pm3\)
b: \(9x^2=16\)
=>\(\left[{}\begin{matrix}3x=4\\3x=-4\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{4}{3}\\x=-\dfrac{4}{3}\end{matrix}\right.\)
c: \(\left(x+2\right)^2=16\)
=>\(\left[{}\begin{matrix}x+2=4\\x+2=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-6\end{matrix}\right.\)
d: \(x^2-9+\left(x-3\right)=0\)
=>\(\left(x-3\right)\left(x+3\right)+\left(x-3\right)=0\)
=>\(\left(x-3\right)\left(x+3+1\right)=0\)
=>\(\left(x-3\right)\left(x+4\right)=0\)
=>\(\left[{}\begin{matrix}x-3=0\\x+4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-4\end{matrix}\right.\)
Bài 2:
a: ĐKXĐ: x>0
\(\sqrt{x}=21\)
=>\(x=21^2\)
=>\(x=441\)
b: ĐKXĐ: x>=0
\(2\sqrt{x}=-1\)
=>\(\sqrt{x}=-\dfrac{1}{2}\)(vô lý)
Vậy: \(x\in\varnothing\)
c: ĐKXĐ: x>=0
\(\left(\sqrt{x}+1\right)^2=4\)
=>\(\left[{}\begin{matrix}\sqrt{x}+1=2\\\sqrt{x}+1=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=1\\\sqrt{x}=-3\left(loại\right)\end{matrix}\right.\)
=>\(\sqrt{x}=1\)
=>x=1(nhận)
d: ĐKXĐ: x>=0
\(\left|\sqrt{x}-1\right|=2\)
=>\(\left[{}\begin{matrix}\sqrt{x}-1=2\\\sqrt{x}-1=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=3\\\sqrt{x}=-1\left(loại\right)\end{matrix}\right.\)
=>\(\sqrt{x}=3\)
=>x=9(nhận)
e: ĐKXĐ: \(x\in R\)
\(\sqrt{x^2-6x+9}=5x-2\)
=>\(\sqrt{\left(x-3\right)^2}=5x-2\)
=>\(\left\{{}\begin{matrix}5x-2>=0\\\left(5x-2\right)^2=\left(x-3\right)^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=\dfrac{2}{5}\\\left(5x-2\right)^2-\left(x-3\right)^2=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{2}{5}\\\left(5x-2-x+3\right)\left(5x-2+x-3\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{2}{5}\\\left(4x+1\right)\left(6x-5\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=\dfrac{2}{5}\\\left[{}\begin{matrix}x=-\dfrac{1}{4}\left(loại\right)\\x=\dfrac{5}{6}\left(nhận\right)\end{matrix}\right.\end{matrix}\right.\)
Vậy: x=5/6
f: \(\sqrt{\left(x-1\right)^2}=3-2x\)
=>\(\left\{{}\begin{matrix}3-2x>=0\\\left(3-2x\right)^2=\left(x-1\right)^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< =\dfrac{3}{2}\\\left(2x-3\right)^2-\left(x-1\right)^2=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< =\dfrac{3}{2}\\\left(2x-3-x+1\right)\left(2x-3+x-1\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< =\dfrac{3}{2}\\\left(x-2\right)\left(3x-4\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< =\dfrac{3}{2}\\\left[{}\begin{matrix}x=2\left(loại\right)\\x=\dfrac{4}{3}\left(nhận\right)\end{matrix}\right.\end{matrix}\right.\)