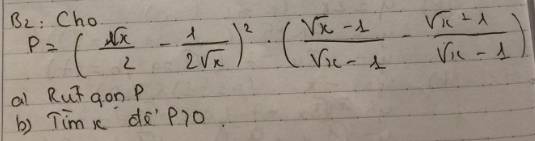Bài 8: Rút gọn biểu thức chứa căn bậc hai

b: 

ĐKXĐ: x>=4

\(5\sqrt{4x-16}-\dfrac{7}{3}\cdot\sqrt{9x-36}=36-3\sqrt{x-4}\)

=>\(5\cdot2\cdot\sqrt{x-4}-\dfrac{7}{3}\cdot3\cdot\sqrt{x-4}+3\sqrt{x-4}=36\)

=>\(6\sqrt{x-4}=36\)

=>\(\sqrt{x-4}=6\)

=>x-4=36

=>x=40

Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề của bạn hơn nhé.

6:

\(P=\dfrac{x-2\sqrt{x}+2\sqrt{x}+4}{x-4}\cdot\dfrac{\sqrt{x}+2}{x+4}\)

\(=\dfrac{x+4}{x+4}\cdot\dfrac{\sqrt{x}+2}{x-4}=\dfrac{1}{\sqrt{x}-2}\)

5:

\(Q=\left(\dfrac{a}{\sqrt{a}\left(\sqrt{a}-2\right)}+\dfrac{a}{\sqrt{a}-2}\right)\cdot\dfrac{\left(\sqrt{a}-2\right)^2}{\sqrt{a}+1}\)

\(=\dfrac{a+\sqrt{a}}{\sqrt{a}+1}\cdot\dfrac{\left(\sqrt{a}-2\right)^2}{\sqrt{a}-2}=\sqrt{a}\left(\sqrt{a}-2\right)\)

4:

\(P=\dfrac{\sqrt{2x}\cdot\sqrt{x}}{\sqrt{2x}\left(\sqrt{x}+\sqrt{2}\right)}+\dfrac{\sqrt{2}\left(\sqrt{x}-\sqrt{2}\right)}{x-2}\)

\(=\dfrac{\sqrt{x}}{\sqrt{x}+\sqrt{2}}+\dfrac{\sqrt{2}}{\sqrt{x}+\sqrt{2}}=1\)

\(P=\dfrac{x+1}{x^2}\left(x\ne0\right)\)

\(=\dfrac{1}{x}+\dfrac{1}{x^2}\)

\(=\left[\left(\dfrac{1}{x}\right)^2+2\cdot\dfrac{1}{x}\cdot\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2\right]-\left(\dfrac{1}{2}\right)^2\)

\(=\left(\dfrac{1}{x}+\dfrac{1}{2}\right)^2-\dfrac{1}{4}\ge-\dfrac{1}{4}\)

Vậy: \(P_{Min}=-\dfrac{1}{4}\Leftrightarrow x=-2\)

\(=\sqrt{13+30\sqrt{2+2\sqrt{2}+1}}\)

\(=\sqrt{13+30\left(\sqrt{2}+1\right)}=\sqrt{43+30\sqrt{2}}\)

\(=\sqrt{43+2\cdot\sqrt{450}}\)

\(=\sqrt{25+2\cdot5\cdot3\sqrt{2}+18}\)

\(=\sqrt{\left(5+3\sqrt{2}\right)^2}=5+3\sqrt{2}\)

Sửa đề: \(\sqrt{9x^2+18}+2\sqrt{x^2+2}-\sqrt{16x^2+32}-12-5=0\)

\(\Leftrightarrow3\sqrt{x^2+2}+2\sqrt{x^2+2}-4\sqrt{x^2+2}=17\)

=>\(\sqrt{x^2+2}=17\)

=>x^2+2=289

=>x^2=287

=>\(x=\pm\sqrt{287}\)

2: \(\dfrac{\sqrt{12}-\sqrt{5}}{\sqrt{2}-1}-\dfrac{1}{\sqrt{5}-2}\)

\(=\left(2\sqrt{3}-\sqrt{5}\right)\left(\sqrt{2}+1\right)-\sqrt{5}-2\)

\(=2\sqrt{6}+2\sqrt{3}-\sqrt{10}-\sqrt{5}-\sqrt{5}-2\)

\(=2\sqrt{6}+2\sqrt{3}-\sqrt{10}-2\sqrt{5}-2\)

3: \(=2\cdot3\sqrt{3}-6\cdot\dfrac{1}{\sqrt{3}}+2-\sqrt{3}-3\sqrt{3}\)

\(=6\sqrt{3}-2\sqrt{3}+2-4\sqrt{3}=2\)

1) \(\dfrac{3+\sqrt{3}}{\sqrt{5}}-\dfrac{2}{\sqrt{3}-1}\)

\(=\dfrac{\sqrt{5}\cdot\left(3+\sqrt{3}\right)}{\sqrt{5}\cdot\sqrt{5}}-\dfrac{2\left(\sqrt{3}+1\right)}{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}\)

\(=\dfrac{3\sqrt{5}+\sqrt{15}}{5}-\dfrac{2\left(\sqrt{3}-1\right)}{3-1}\)

\(=\dfrac{3\sqrt{5}+\sqrt{15}}{5}-\left(\sqrt{3}-1\right)\)

\(=\dfrac{3\sqrt{5}+\sqrt{15}-5\sqrt{3}+5}{5}\)

2) \(\dfrac{\sqrt{12}-\sqrt{5}}{\sqrt{2}-1}-\dfrac{1}{\sqrt{5}-2}\)

\(=\dfrac{\left(2\sqrt{3}-\sqrt{5}\right)\left(\sqrt{2}+1\right)}{\left(\sqrt{2}-1\right)\left(\sqrt{2}+1\right)}-\dfrac{\sqrt{5}+2}{\left(\sqrt{5}-2\right)\left(\sqrt{5}+2\right)}\)

\(=\dfrac{2\sqrt{6}+2\sqrt{3}-\sqrt{10}-\sqrt{5}}{2-1}-\dfrac{\sqrt{5}+2}{5-4}\)

\(=2\sqrt{6}+2\sqrt{3}-\sqrt{10}-\sqrt{5}-\left(\sqrt{5}+2\right)\)

\(=2\sqrt{6}+2\sqrt{3}-\sqrt{10}-2\sqrt{5}-2\)

3) \(2\sqrt{27}-6\sqrt{\dfrac{1}{3}}+\dfrac{1}{2}+\dfrac{\sqrt{3}-9}{\sqrt{3}}\)

\(=2\cdot3\sqrt{3}-\dfrac{6}{\sqrt{3}}+\dfrac{1}{2}+\dfrac{\sqrt{3}\left(1-3\sqrt{3}\right)}{\sqrt{3}}\)

\(=6\sqrt{3}-\dfrac{\sqrt{3}\cdot2\sqrt{3}}{\sqrt{3}}+\dfrac{1}{2}+1-3\sqrt{3}\)

\(=6\sqrt{3}-2\sqrt{3}+\dfrac{1}{2}+1-3\sqrt{3}\)

\(=\dfrac{1}{2}+1+\sqrt{3}\)

\(=\dfrac{3}{2}+\sqrt{3}\)

1: \(\dfrac{1}{3-2\sqrt{2}}+\dfrac{1}{\sqrt{5}+2}\)

\(=\dfrac{3+2\sqrt{2}}{1}+\dfrac{\sqrt{5}-2}{1}\)

\(=3+2\sqrt{2}+\sqrt{5}-2=2\sqrt{2}+\sqrt{5}+1\)

2: \(\dfrac{1}{\sqrt{3}+\sqrt{7}}+\dfrac{2}{1-\sqrt{7}}\)

\(=\dfrac{\sqrt{7}-\sqrt{3}}{4}+\dfrac{2\left(1+\sqrt{7}\right)}{-6}\)

\(=\dfrac{\sqrt{7}-\sqrt{3}}{4}-\dfrac{1+\sqrt{7}}{3}\)

\(=\dfrac{3\left(\sqrt{7}-\sqrt{3}\right)-4\left(\sqrt{7}+1\right)}{12}=\dfrac{-\sqrt{7}-3\sqrt{3}-4}{12}\)

3:

\(=\dfrac{\sqrt{a}\left(\sqrt{a}-2\right)}{2-\sqrt{a}}=-\dfrac{\sqrt{a}\left(\sqrt{a}-2\right)}{\sqrt{a}-2}=-\sqrt{a}\)

4:

\(=\dfrac{\sqrt{xy}\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{x}+\sqrt{y}}\)

\(=\sqrt{xy}\)

1) \(\dfrac{1}{3-2\sqrt{2}}+\dfrac{1}{\sqrt{5}+2}\)

\(=\dfrac{3+2\sqrt{2}}{\left(3-2\sqrt{2}\right)\left(3+2\sqrt{2}\right)}+\dfrac{\sqrt{5}-2}{\left(\sqrt{5}+2\right)\left(\sqrt{5}-2\right)}\)

\(=\dfrac{3+2\sqrt{2}}{3^2-\left(2\sqrt{2}\right)^2}+\dfrac{\sqrt{5}-2}{\left(\sqrt{5}\right)^2-2^2}\)

\(=\dfrac{3+2\sqrt{2}}{1}+\dfrac{\sqrt{5}-2}{1}\)

\(=3+2\sqrt{2}+\sqrt{5}-2\)

\(=2\sqrt{2}+\sqrt{5}+1\)

2) \(\dfrac{1}{\sqrt{3}-\sqrt{7}}+\dfrac{2}{1-\sqrt{7}}\)

\(=\dfrac{\sqrt{3}+\sqrt{7}}{\left(\sqrt{3}+\sqrt{7}\right)\left(\sqrt{3}-\sqrt{7}\right)}+\dfrac{2\cdot\left(1+\sqrt{7}\right)}{\left(1-\sqrt{7}\right)\left(1+\sqrt{7}\right)}\)

\(=\dfrac{\sqrt{3}+\sqrt{7}}{\left(\sqrt{3}\right)^2-\left(\sqrt{7}\right)^2}+\dfrac{2\cdot\left(1+\sqrt{7}\right)}{1^2-\left(\sqrt{7}\right)^2}\)

\(=\dfrac{-\sqrt{3}-\sqrt{7}}{4}-\dfrac{2\cdot\left(1+\sqrt{7}\right)}{6}\)

\(=\dfrac{-\sqrt{3}-\sqrt{7}}{4}-\dfrac{1+\sqrt{7}}{3}\)

\(=\dfrac{-3\sqrt{3}-3\sqrt{7}}{12}-\dfrac{4+4\sqrt{7}}{12}\)

\(=\dfrac{-3\sqrt{3}-3\sqrt{7}-4-4\sqrt{7}}{12}\)

\(=\dfrac{-3\sqrt{3}-7\sqrt{7}-4}{12}\)

3) \(\dfrac{a-2\sqrt{a}}{2-\sqrt{a}}\)

\(=-\dfrac{a-2\sqrt{a}}{\sqrt{a}-2}\)

\(=-\dfrac{\sqrt{a}\cdot\left(\sqrt{a}-2\right)}{\sqrt{a}-2}\)

\(=-\sqrt{a}\)

4) \(\dfrac{x\sqrt{y}+y\sqrt{x}}{\sqrt{x}+\sqrt{y}}\)

\(=\dfrac{\sqrt{x}\cdot\sqrt{xy}+\sqrt{y}\cdot\sqrt{xy}}{\sqrt{x}+\sqrt{y}}\)

\(=\dfrac{\sqrt{xy}\cdot\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{x}+\sqrt{y}}\)

\(=\sqrt{xy}\)

a: \(P=\left(\dfrac{x-1}{2\sqrt{x}}\right)^2\cdot\dfrac{\sqrt{x}-1-\sqrt{x}-1}{\left(\sqrt{x}-1\right)}\)

\(=\dfrac{\left(x-1\right)^2}{4x}\cdot\dfrac{-2}{\sqrt{x}-1}=\dfrac{-1}{2x}\cdot\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2\)

b: P>0

=>\(-\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}{2x}>0\)

=>\(-\left(\sqrt{x}-1\right)>0\)

=>căn x<1

=>0<x<1

a) \(P=\left(\dfrac{\sqrt{x}}{2}-\dfrac{1}{2\sqrt{x}}\right)^2\cdot\left(\dfrac{\sqrt{x}-1}{\sqrt{x}-1}+\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\right)\) (ĐK: \(x>0;x\ne1\)) 

\(P=\left[\dfrac{\sqrt{x}\cdot\sqrt{x}}{2\sqrt{x}}-\dfrac{1}{2\sqrt{x}}\right]^2\cdot\dfrac{\sqrt{x}-1-\sqrt{x}-1}{\sqrt{x}-1}\)

\(P=\left(\dfrac{x-1}{2\sqrt{x}}\right)^2\cdot\dfrac{-2}{\sqrt{x}-1}\)

\(P=\dfrac{\left(\sqrt{x}+1\right)^2\left(\sqrt{x}-1\right)^2}{4x}\cdot\dfrac{-2}{\sqrt{x}-1}\)

\(P=\dfrac{\left(\sqrt{x}+1\right)^2\left(x-1\right)}{-2x}\)

b) P > 0 khi:

\(\dfrac{\left(\sqrt{x}+1\right)^2\left(\sqrt{x}-1\right)}{-\sqrt{x}}>0\) 

Mà \(-2x\le0\) và \(\left(\sqrt{x}+1\right)^2>0\) nên: 

\(\sqrt{x}-1< 0\)

\(\Leftrightarrow\sqrt{x}< 1\)

\(\Leftrightarrow x< 1\)

Kết hợp với đk:

Vậy: P > 0 khi: 

\(0< x< 1\)