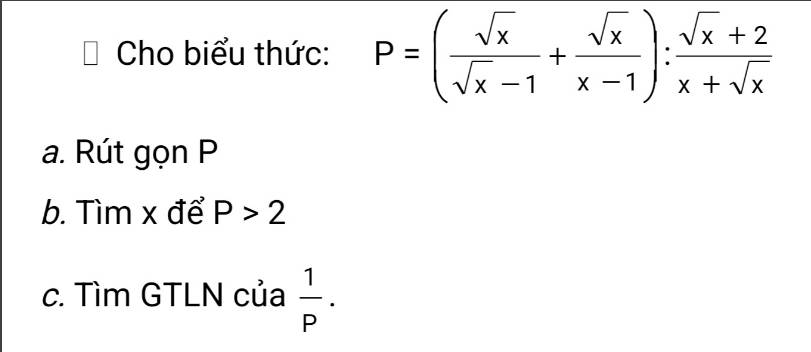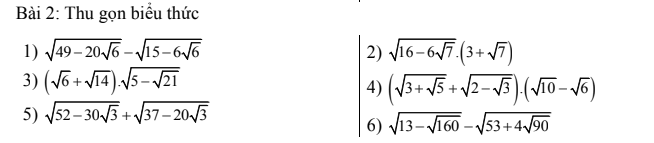Lời giải:
a. ĐKXĐ: $x>0; x\neq 1$
\(P=\left[\frac{\sqrt{x}(\sqrt{x}+1)}{(\sqrt{x}-1)(\sqrt{x}+1)}+\frac{\sqrt{x}}{(\sqrt{x}-1)(\sqrt{x}+1)}\right].\frac{x+\sqrt{x}}{\sqrt{x}+2}\)
\(=\frac{x+\sqrt{x}+\sqrt{x}}{(\sqrt{x}-1)(\sqrt{x}+1)}.\frac{\sqrt{x}(\sqrt{x}+1)}{\sqrt{x}+2}=\frac{\sqrt{x}(\sqrt{x}+2)}{(\sqrt{x}-1)(\sqrt{x}+1)}.\frac{\sqrt{x}(\sqrt{x}+1)}{\sqrt{x}+2}=\frac{x}{\sqrt{x}-1}\)
b.
$P>2 \Leftrightarrow \frac{x}{\sqrt{x}-1}-2>0$
$\Leftrightarrow \frac{x-2\sqrt{x}+2}{\sqrt{x}-1}>0$
$\Leftrightarrow \frac{(\sqrt{x}-1)^2+1}{\sqrt{x}-1}>0$
$\Leftrightarrow \sqrt{x}-1>0$ (do $(\sqrt{x}-1)^2+1>0$)
$\Leftrightarrow x>1$
Kết hợp đkxđ suy ra $x>1$
c.
$\frac{1}{P}=\frac{\sqrt{x}-1}{x}$
Áp dụng BĐT Cô-si:
$x+4\geq 4\sqrt{x}\Rightarrow x\geq 4(\sqrt{x}-1)$
$\Rightarrow \frac{\sqrt{x}-1}{x}\leq \frac{\sqrt{x}-1}{4(\sqrt{x}-1)}=\frac{1}{4}$
Vậy $\frac{1}{P}$ max $=\frac{1}{4}$ khi $x=4$