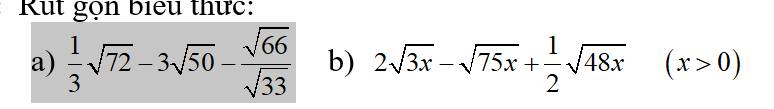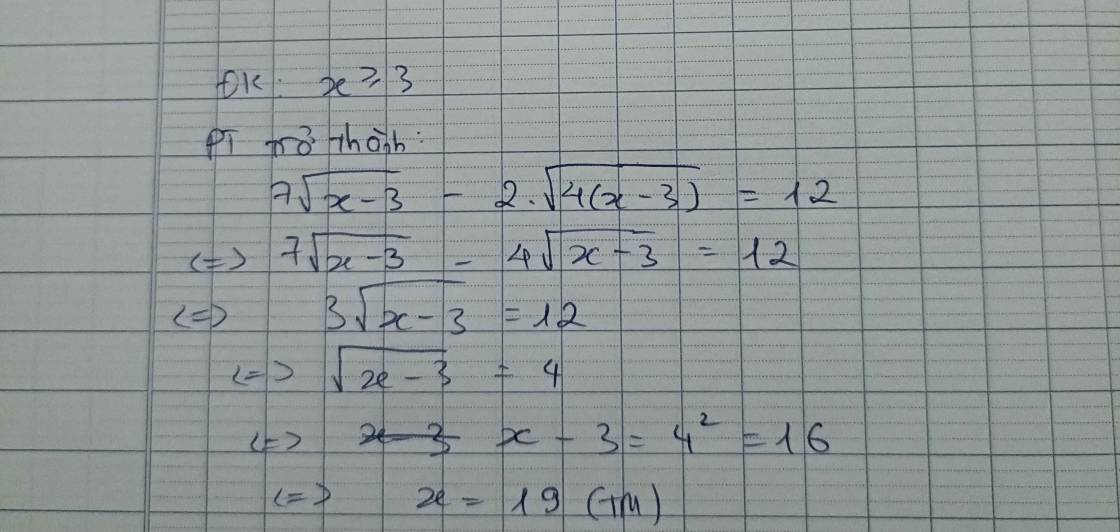P = (sqrt(x))/(sqrt(x) + 1) - 2/(x - 1) + 2/(sqrt(x) - 1) * v_{i}x20 và x ne1
Bài 8: Rút gọn biểu thức chứa căn bậc hai
Bạn nên gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để được hỗ trợ tốt hơn nhé. Đọc đề ntn khó hiểu lắm.
Đúng 0
Bình luận (0)
(1/(sqrt(x) + 2) - 1/(2 - sqrt(x)) + x/(x - 4)) / (1 + 4/(sqrt(x) - 2))
Bạn nên viết đầy đủ yêu cầu đề và gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề hơn.
Đúng 0
Bình luận (0)
ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x< >4\end{matrix}\right.\)
\(\left(\dfrac{1}{\sqrt{x}+2}-\dfrac{1}{2-\sqrt{x}}+\dfrac{x}{x-4}\right):\left(1+\dfrac{4}{\sqrt{x}-2}\right)\)
\(=\left(\dfrac{1}{\sqrt{x}+2}+\dfrac{1}{\sqrt{x}-2}+\dfrac{x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\right):\dfrac{\sqrt{x}-2+4}{\sqrt{x}-2}\)
\(=\dfrac{\sqrt{x}-2+\sqrt{x}+2+x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\)
\(=\dfrac{x+2\sqrt{x}}{\left(\sqrt{x}+2\right)^2}=\dfrac{\sqrt{x}}{\sqrt{x}+2}\)
Đúng 0
Bình luận (0)
(sqrt(x) - 1)/(sqrt(x) - 2) + (2sqrt(x))/(sqrt(x) + 2) - (3sqrt(x) - 2)/(x - 4)
\(\dfrac{\sqrt{x}-1}{\sqrt{x}-2}+\dfrac{2\sqrt{x}}{\sqrt{x}+2}-\dfrac{3\sqrt{x}-2}{x-4}\left(dkxd:x\ge0;x\ne4\right)\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{2\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}-\dfrac{3\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{x+\sqrt{x}-2+2x-4\sqrt{x}-3\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{3x-6\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{3\sqrt{x}}{\sqrt{x}+2}\)
\(\text{#}Toru\)
Đúng 3
Bình luận (0)
(\(\dfrac{\sqrt{a}}{\sqrt{a}-1}\)-\(\dfrac{2\sqrt{a}}{a-\sqrt{a}}\)):\(\dfrac{\sqrt{a}+1}{a-1}\) mọi người giúp em với ạ
ĐKXĐ: \(a>0;a\ne1\)
\(\left(\dfrac{\sqrt{a}}{\sqrt{a}-1}-\dfrac{2\sqrt{a}}{a-\sqrt{a}}\right):\dfrac{\sqrt{a}+1}{a-1}\)
\(=\left(\dfrac{\sqrt{a}}{\sqrt{a}-1}-\dfrac{2\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-1\right)}\right).\dfrac{a-1}{\sqrt{a}+1}\)
\(=\left[\dfrac{\sqrt{a}.\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-1\right)}-\dfrac{2\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-1\right)}\right].\dfrac{a-1}{\sqrt{a}+1}\)
\(=\left[\dfrac{\sqrt{a}\left(\sqrt{a}-2\right)}{\sqrt{a}\left(\sqrt{a}-1\right)}\right].\dfrac{a-1}{\sqrt{a}+1}\)
\(=\dfrac{\sqrt{a}-2}{\sqrt{a}-1}.\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\)
\(=\sqrt{a}-2\)
Đúng 2
Bình luận (1)
Kết quả trục căn thức 3/(5-√3) là: A.(5-√3)/3 B.(5+√3)/3 C.(5-√3)/4 D.(5+√3)/4
\(\dfrac{3}{5-\sqrt{3}}=\dfrac{3\left(5+\sqrt{3}\right)}{\left(5-\sqrt{3}\right)\left(5+\sqrt{3}\right)}\)
\(=\dfrac{3\left(5+\sqrt{3}\right)}{5^2-\left(\sqrt{3}\right)^2}=\dfrac{3\left(5+\sqrt{3}\right)}{25-3}=\dfrac{3\left(5+\sqrt{3}\right)}{22}\)
Đúng 0
Bình luận (0)
\(\sqrt{x^2-9}-3\sqrt{x-3=0}\)
\(\sqrt{x^2-9}-3\sqrt{x-3}=0\\ \Leftrightarrow\sqrt{\left(x-3\right)\left(x+3\right)}-3\sqrt{x-3}=0\\ \Leftrightarrow\sqrt{x-3}\cdot\sqrt{x+3}-3\sqrt{x-3}=0\\ \Leftrightarrow\left(\sqrt{x-3}\right)\left(\sqrt{x+3}-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}\sqrt{x-3}=0\\\sqrt{x+3}-3=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}\sqrt{x-3}=0\\\sqrt{x+3}=3\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+3=9\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=3\\x=6\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Sửa đề: \(\sqrt{x^2-9}-3\sqrt{x-3}=0\)
ĐKXĐ: \(\left\{{}\begin{matrix}x^2-9>=0\\x-3>=0\end{matrix}\right.\)
=>x>=3
\(\sqrt{x^2-9}-3\sqrt{x-3}=0\)
=>\(\sqrt{x-3}\cdot\sqrt{x+3}-3\sqrt{x-3}=0\)
=>\(\sqrt{x-3}\left(\sqrt{x+3}-3\right)=0\)
=>\(\left[{}\begin{matrix}x-3=0\\x+3=9\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\left(nhận\right)\\x=6\left(nhận\right)\end{matrix}\right.\)
Đúng 0
Bình luận (0)
ĐKXĐ: x ≥ 3
Phương trình tương đương:
√[(x - 3)(x + 3)] - 3√(x - 3) = 0
⇔ √(x - 3)[√(x + 3) - 3] = 0
⇔ √(x - 3) = 0 hoặc √(x + 3) - 3 = 0
*) √(x - 3) = 0
⇔ x - 3 = 0
⇔ x = 3 (nhận)
*) √(x + 3) - 3 = 0
⇔ √(x + 3) = 3
⇔ x + 3 = 9
⇔ x = 9 - 3
⇔ x = 6 (nhận)
Vậy S = {3; 6}
Đúng 0
Bình luận (0)
a: \(\dfrac{1}{3}\cdot\sqrt{72}-3\sqrt{50}-\dfrac{\sqrt{66}}{\sqrt{33}}\)
\(=\dfrac{1}{3}\cdot6\sqrt{2}-3\cdot5\sqrt{2}-\sqrt{2}\)
\(=2\sqrt{2}-15\sqrt{2}-\sqrt{2}=-14\sqrt{2}\)
b: \(2\sqrt{3x}-\sqrt{75x}+\dfrac{1}{2}\cdot\sqrt{48x}\)
\(=2\sqrt{3x}-5\sqrt{3x}+\dfrac{1}{2}\cdot4\sqrt{3x}\)
\(=-3\sqrt{3x}+2\sqrt{3x}=-\sqrt{3x}\)
Đúng 1
Bình luận (0)
\(\dfrac{1}{3}\sqrt{72}-3\sqrt{50}-\dfrac{\sqrt{66}}{\sqrt{33}}\\ =\dfrac{1}{3}\sqrt{36\cdot2}-3\sqrt{25\cdot2}-\sqrt{\dfrac{66}{33}}\\ =\dfrac{1}{3}\cdot6\sqrt{2}-3\cdot5\sqrt{2}-\sqrt{2}\\ =2\sqrt{2}-15\sqrt{2}-\sqrt{2}\\ =-14\sqrt{2}\)
\(b,2\sqrt{3x}-\sqrt{75x}+\dfrac{1}{2}\sqrt{48x}\\ =2\sqrt{3x}-\sqrt{25\cdot3x}+\dfrac{1}{2}\sqrt{16\cdot3}\\ =2\sqrt{3x}-5\sqrt{3x}+\dfrac{1}{2}\cdot4\sqrt{3x}\\ =2\sqrt{3x}-5\sqrt{3x}+2\sqrt{3x}\\ =-\sqrt{3x}\)
Đúng 1
Bình luận (0)
\(7\sqrt{x-3}-2\sqrt{4x-12}=12\)
ĐKXĐ: x ≥ 3
Phương trình tương đương:
7√(x - 3) - 2.2√(x - 3) = 12
⇔ 7√(x - 3) - 4√(x - 3) = 12
⇔ 3√(x - 3) = 12
⇔ √(x - 3) = 12 : 3
⇔ √(x - 3) = 4
⇒ x - 3 = 16
⇔ x = 16 + 3
⇔ x = 19 (nhận)
Vậy S = {19}
Đúng 2
Bình luận (0)
\(7\sqrt{x-3}-2\sqrt{4x-12}=12\\ \Leftrightarrow7\sqrt{x-3}-2\sqrt{4\left(x-3\right)}=12\\ \Leftrightarrow7\sqrt{x-3}-4\sqrt{x-3}=12\\ \Leftrightarrow3\sqrt{x-3}=12\\ \Leftrightarrow\sqrt{x-3}=\dfrac{12}{3}\\ \Leftrightarrow\sqrt{x-3}=4\\ \Leftrightarrow\left(\sqrt{x-3}\right)^2=4^2\\ \Leftrightarrow x-3=16\\ \Leftrightarrow x=16+3\\ \Leftrightarrow x=19.\)
Đúng 1
Bình luận (0)
\(\sqrt{x-1}+2=5\)
2Cho biểu thức (với x 0; x ¹ 1) a) Rút gọn biểu thức A.GIÚP TỚ VỚI Ạ PLSSSS
Đọc tiếp
2Cho biểu thức 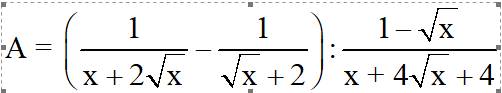
(với x > 0; x ¹ 1)
a) Rút gọn biểu thức A.
GIÚP TỚ VỚI Ạ PLSSSS
\(A=\left(\dfrac{1}{x+2\sqrt{x}}-\dfrac{1}{\sqrt{x}+2}\right):\dfrac{1-\sqrt{x}}{x+4\sqrt{x}+4}\left(x>0;x\ne1\right)\)
\(A=\left[\dfrac{1}{\sqrt{x}\left(\sqrt{x}+2\right)}-\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)}\right]:\dfrac{1-\sqrt{x}}{\left(\sqrt{x}\right)^2+2\cdot\sqrt{x}\cdot2+2^2}\)
\(A=\dfrac{1-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)}:\dfrac{1-\sqrt{x}}{\left(\sqrt{x}+2\right)^2}\)
\(A=\dfrac{1-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)}\cdot\dfrac{\left(\sqrt{x}+2\right)^2}{1-\sqrt{x}}\)
\(A=\dfrac{\left(\sqrt{x}+2\right)^2}{\sqrt{x}\left(\sqrt{x}+2\right)}\)
\(A=\dfrac{\sqrt{x}+2}{\sqrt{x}}\)
Vậy: ...
Đúng 1
Bình luận (0)