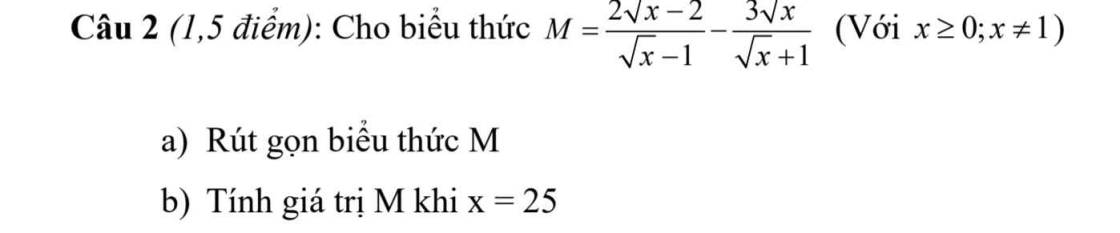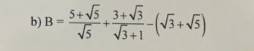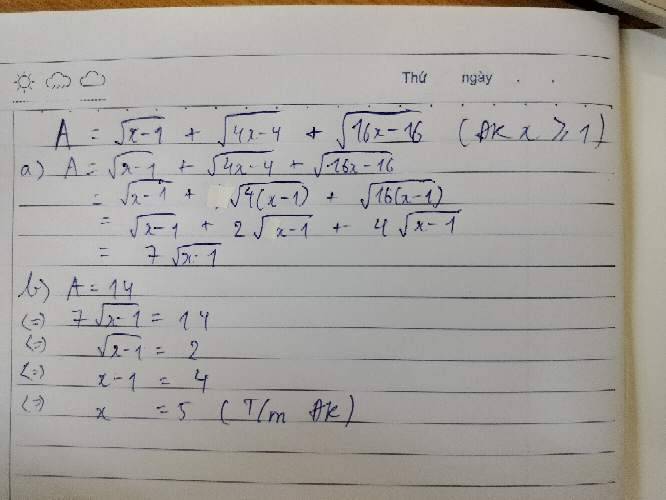Bài 8: Rút gọn biểu thức chứa căn bậc hai

1: \(A=\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{x-1}\right)\cdot\left(\dfrac{x-\sqrt{x}}{2\sqrt{x}+1}\right)\)

\(=\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{2\sqrt{x}+1}\)

\(=\dfrac{\sqrt{x}+1+\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{2\sqrt{x}+1}\)

\(=\dfrac{\sqrt{x}}{\sqrt{x}+1}\)

2: Thay x=9 vào A, ta được:

\(A=\dfrac{3}{3+1}=\dfrac{3}{4}\)

\(\dfrac{1}{\sqrt{x}+3}-\dfrac{\sqrt{x}-3}{x-9}\)

\(=\dfrac{1}{\sqrt{x}+3}-\dfrac{\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)

\(=\dfrac{1}{\sqrt{x}+3}-\dfrac{1}{\sqrt{x}+3}=0\)

\(\sqrt{75}+\sqrt{48}+\sqrt{300}\)

\(=5\sqrt{3}+4\sqrt{3}+10\sqrt{3}\)

\(=19\sqrt{3}\)

\(\sqrt{13^2}=\left|13\right|=13\)

a: \(M=\dfrac{2\sqrt{x}-2}{\sqrt{x}-1}-\dfrac{3\sqrt{x}}{\sqrt{x}+1}\)

\(=\dfrac{2\left(\sqrt{x}-1\right)}{\sqrt{x}-1}-\dfrac{3\sqrt{x}}{\sqrt{x}+1}\)

\(=2-\dfrac{3\sqrt{x}}{\sqrt{x}+1}=\dfrac{2\left(\sqrt{x}+1\right)-3\sqrt{x}}{\sqrt{x}+1}\)

\(=\dfrac{2\sqrt{x}+2-3\sqrt{x}}{\sqrt{x}+1}=\dfrac{-\sqrt{x}+2}{\sqrt{x}+1}\)

b: Khi x=25 thì \(M=\dfrac{-\sqrt{25}+2}{\sqrt{25}+1}=\dfrac{-5+2}{5+1}=\dfrac{-3}{6}=-\dfrac{1}{2}\)

\(B=\dfrac{5+\sqrt{5}}{\sqrt{5}}+\dfrac{3+\sqrt{3}}{\sqrt{3}+1}-\left(\sqrt{3}+\sqrt{5}\right)\)

\(=\dfrac{\sqrt{5}\left(\sqrt{5}+1\right)}{\sqrt{5}}+\dfrac{\sqrt{3}\left(\sqrt{3}+1\right)}{\sqrt{3}+1}-\sqrt{3}-\sqrt{5}\)

\(=\sqrt{5}+1+\sqrt{3}-\sqrt{3}-\sqrt{5}\)

=1

\(B=\dfrac{5+\sqrt{5}}{\sqrt{5}}+\dfrac{3+\sqrt{3}}{\sqrt{3}+1}-\left(\sqrt{3}+\sqrt{5}\right)\\ =\dfrac{\sqrt{5}\left(\sqrt{5}+1\right)}{\sqrt{5}}+\dfrac{\sqrt{3}\left(\sqrt{3}+1\right)}{\sqrt{3}+1}-\left(\sqrt{3}+\sqrt{5}\right)\\ =\sqrt{5}+1+\sqrt{3}-\sqrt{3}-\sqrt{5}\\ =1\)

ĐKXĐ: x ≥ 0

Do -2 < 2

⇒ √x - 2 < √x + 2

⇒ (√x - 2)/(√x + 2) < 1

Vậy A < 1

\(A=\dfrac{\sqrt{x}-2}{\sqrt{x}+2}=\dfrac{\sqrt{x}+2-4}{\sqrt{x}+2}=1-\dfrac{4}{\sqrt{x}+2}\left(dkxd:x\ge0\right)\)

Ta thấy: \(\sqrt{x}+2>0\forall x\ge0\)

\(\Rightarrow\dfrac{4}{\sqrt{x}+2}>0\forall x\ge0\)

\(\Rightarrow-\dfrac{4}{\sqrt{x}+2}< 0\forall x\ge0\)

\(\Rightarrow A=1-\dfrac{4}{\sqrt{x}+2}< 1\forall x\ge0\left(dpcm\right)\)

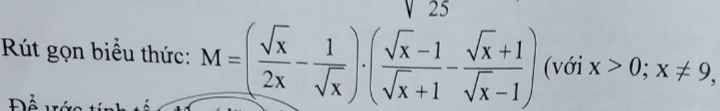
\(M=\left(\dfrac{\sqrt{x}}{2x}-\dfrac{1}{\sqrt{x}}\right)\cdot\left(\dfrac{\sqrt{x}-1}{\sqrt{x}+1}-\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\right)\\ =\left(\dfrac{\sqrt{x}}{2x}-\dfrac{2\sqrt{x}}{2x}\right)\cdot\left(\dfrac{\left(\sqrt{x}-1\right)^2-\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\\ =\dfrac{x-2\sqrt{x}}{2x}\cdot\dfrac{x-2\sqrt{x}+1-\left(x+2\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{2x}\cdot\dfrac{x-2\sqrt{x}+1-x-2\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{2x}\cdot\dfrac{-4\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)

\(=\dfrac{-2\left(\sqrt{x}-2\right)}{x-1}\)

\(\left(\dfrac{x+\sqrt{x}+1}{x\sqrt{x}-1}+\dfrac{1}{\sqrt{x}-1}\right):\dfrac{6}{x-1}\\ =\left(\dfrac{x+\sqrt{x}+1}{\left(\sqrt{x}\right)^3-1}+\dfrac{1}{\sqrt{x}-1}\right)\cdot\dfrac{x-1}{6}\\ =\left(\dfrac{x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{1}{\sqrt{x}-1}\right)\cdot\dfrac{x-1}{6}\\ =\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{1}{\sqrt{x}-1}\right)\cdot\dfrac{x-1}{6}\\ =\dfrac{2}{\sqrt{x}-1}\cdot\dfrac{x-1}{6}\\ =\dfrac{\sqrt{x}+1}{3}\)

Bạn nên gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề của bạn hơn nhé.