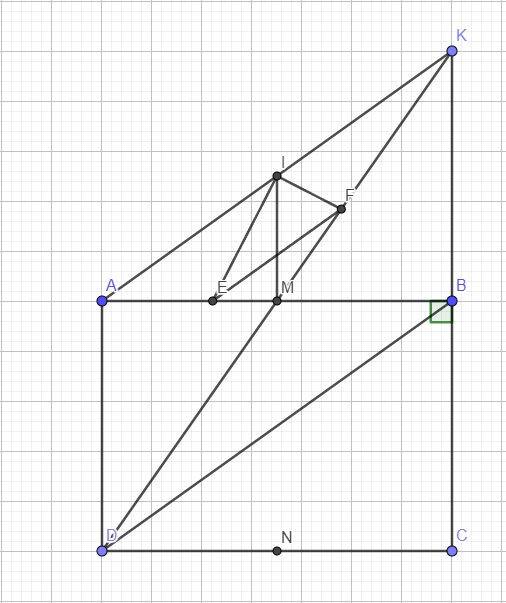
Cho hình chữ nhật ABCD(AB>AD), gọi M là trung điểm cạnh AB. Từ M kẻ MN vuông góc với CD tại N( N thuộc CD)
a, Trên tia DM lấy điểm K sao cho M là trung điểm của đoạn thẳng DK. Chứng minh tứ giác ADBK là hình bình hành và tam giác AKC cân.
b,Gọi I là trung điểm của AK. Tia phân giác của góc AIM cắt AM tại E, tia phân giác của góc KIM cắt MK ở F. Chứng minh EF song song với BD.
a.
Xét tứ giác ADBK có: hai đường chéo AB và DK cắt nhau tại trung điểm M của mỗi đường
\(\Rightarrow ADBK\) là hình bình hành
Do ABCD là hình chữ nhật \(\Rightarrow AB\perp BC\Rightarrow AB\) là đường cao tam giác ACK
Theo cmt, ADBK là hbh \(\Rightarrow BK=AD\)
Mà \(AD=BC\) (ABCD là hcn)
\(\Rightarrow BK=BC\Rightarrow AB\) là trung tuyến tam giác ACK
\(\Rightarrow AB\) vừa là đường cao vừa là trung tuyến nên tam giác ACK cân tại A
b.
Do IE là phân giác, áp dụng định lý phân giác trong tam giác IAM:
\(\dfrac{EM}{EA}=\dfrac{IM}{IA}\) (1)
Do IF là phân giác, áp dụng định lý phân giác trong tam giác IMK:
\(\dfrac{FM}{FK}=\dfrac{IM}{IK}\) (2)
Mà I là trung điểm AK \(\Rightarrow IA=IK\) (3)
(1);(2);(3) \(\Rightarrow\dfrac{EM}{EA}=\dfrac{FM}{FK}\Rightarrow EF||AK\) (định lý Talet đảo)
Theo c/m câu a do ADBK là hình bình hành \(\Rightarrow AK||BD\)
\(\Rightarrow EF||BD\)