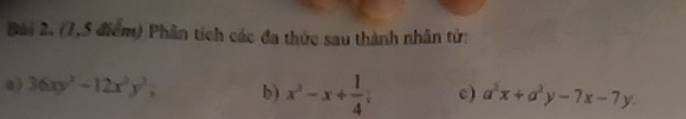Giúp mình đi please
Bài 3: Hình thang cân
a:
ΔABC vuông tại A
mà AM là đường trung tuyến
nên AM=MB=MC
Xét ΔABC có
M là trung điểm của BC
MI//AC
Do đó: I là trung điểm của AB
Xét tứ giác AMBD có
I là trung điểm chung của AB và MD
nên AMBD là hình bình hành
Hình bình hành AMBD có MA=MB
nên AMBD là hình thoi
b: Xét tứ giác AIMH có
AI//MH
AH//MI
Do đó: AIMH là hình bình hành
Hình bình hành AIMH có \(\widehat{HAI}=90^0\)
nên AIMH là hình chữ nhật
=>AI=MH
HM//AB
=>\(\widehat{HMA}=\widehat{MAB}\)(hai góc so le trong)(1)
MA=MB
=>\(\widehat{MAB}=\widehat{MBA}\)
=>\(\widehat{MAB}=\widehat{ABC}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{HMA}=\widehat{ABC}\)
c: Xét ΔABC có
M là trung điểm của BC
MH//AB
Do đó: H là trung điểm của AC
=>\(AH=\dfrac{AC}{2}=6\left(cm\right)\)
I là trung điểm của AB
=>\(AI=\dfrac{AB}{2}=\dfrac{9}{2}=4,5\left(cm\right)\)
AIMH là hình chữ nhật
=>\(S_{AIMH}=AI\cdot AH=4,5\cdot6=27\left(cm^2\right)\)
d:
Xét tứ giác AMCE có
H là trung điểm chung của AC và ME
Do đó: AMCE là hình bình hành
Hình bình hành AMCE có MA=MC
nên AMCE là hình thoi
=>AC là phân giác của góc MAE
AMBD là hình thoi
=>AB là phân giác của góc MAD
\(\widehat{MAE}+\widehat{MAD}=\widehat{EAD}\)
=>\(\widehat{EAD}=2\cdot\widehat{BAM}+2\cdot\widehat{CAM}\)
=>\(\widehat{EAD}=2\cdot\left(\widehat{BAM}+\widehat{CAM}\right)\)
=>\(\widehat{EAD}=2\cdot90^0=180^0\)
=>E,A,D thẳng hàng
Đúng 2
Bình luận (0)
2:
a: ΔABC cân tại A
mà AM là đường phân giác
nên AM\(\perp\)BC và M là trung điểm của BC
Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
nên ABDC là hình bình hành
Hình bình hành ABDC có AB=AC
nên ABDC là hình thoi
b: BF\(\perp\)BC
CE\(\perp\)BC
Do đó: BF//CE
\(\widehat{ABC}+\widehat{ABF}=\widehat{FBC}=90^0\)
\(\widehat{ACB}+\widehat{AFB}=90^0\)(ΔFBC vuông tại B)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{ABF}=\widehat{AFB}\)
=>AB=AF
=>FA=AB
mà AB=AC
nên FA=AC
=>A là trung điểm của FC
\(\widehat{ABC}+\widehat{AEC}=90^0\)(ΔECB vuông tại C)
\(\widehat{ACB}+\widehat{ACE}=\widehat{ECB}=90^0\)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{AEC}=\widehat{ACE}\)
=>AC=AE
mà AC=AB
nên AB=AE
=>A là trung điểm của BE
Xét tứ giác BFEC có
A là trung điểm chung của BE và FC
nên BFEC là hình bình hành
Hình bình hành BFEC có \(\widehat{FBC}=90^0\)
nên BFEC là hình chữ nhật
c: Để hình thoi ABDC trở thành hình vuông thì \(\widehat{BAC}=90^0\)
Đúng 1
Bình luận (0)
a: Xét ΔABC có
M là trung điểm của BC
MI//AC
Do đó: I là trung điểm của AB
Xét tứ giác AMBD có
I là trung điểm chung của AB và MD
nên AMBD là hình bình hành
Hình bình hành AMBD có AB\(\perp\)MD
nên AMBD là hình thoi
b: Xét tứ giác AIMH có
\(\widehat{AIH}=\widehat{AHM}=\widehat{HAI}=90^0\)
=>AIMH là hình chữ nhật
=>AI=MH
ΔABC vuông tại A
mà AM là đường trung tuyến
nên AM=MB=MC
=>MA=MB
=>\(\widehat{MAB}=\widehat{MBA}\)
HM//AB
=>\(\widehat{HMA}=\widehat{MAI}\)
mà \(\widehat{MAI}=\widehat{MBA}\)
nên \(\widehat{HMA}=\widehat{ABC}\)
c: Xét ΔABC có
M là trung điểm của BC
MH//AB
Do đó: H là trung điểm của AC
=>\(AH=\dfrac{AC}{2}=6\left(cm\right)\)
I là trung điểm của AB
=>\(AI=\dfrac{AB}{2}=4,5\left(cm\right)\)
AIMH là hình chữ nhật
=>\(S_{AIMH}=AI\cdot AH=4,5\cdot6=27\left(cm^2\right)\)
d: Xét tứ giác AMCE có
H là trung điểm chung của AC và ME
nên AMCE là hình bình hành
Hình bình hành AMCE có MA=MC
nên AMCE là hình thoi
=>AC là phân giác của \(\widehat{MAE}\)
AMBD là hình thoi
=>AB là phân giác của \(\widehat{MAD}\)
\(\widehat{EAD}=\widehat{EAM}+\widehat{DAM}\)
\(=2\cdot\left(\widehat{BAM}+\widehat{CAM}\right)\)
\(=2\cdot90^0=180^0\)
=>E,A,D thẳng hàng
Đúng 1
Bình luận (0)
Cho hình thang cân MNCD có MN//HD và MN
phân tích đa thức thành nhân tử
36xy^3-12x^2y^2
\(36xy^3-12x^2y^2\)
\(=3\cdot12\cdot x\cdot y^2\cdot y-12\cdot x\cdot x\cdot y^2\)
\(=12xy^2\cdot3y-12xy^2\cdot x\)
\(=12xy^2\cdot\left(3y-x\right)\)
Đúng 0
Bình luận (0)
`#3107.101107`
a)
B ghi lại đề giúp mình.
b)
\(x^2-x+\dfrac{1}{4}\)
`= x^2 - 2*x*1/2 + (1/2)^2`
`= (x - 1/2)^2`
c)
`a^3x + a^3y - 7x - 7y`
`= (a^3x + a^3y)-(7x+7y)`
`= a^3(x+y)-7(x+y)`
`= (x + y)(a^3 + 7).`
Đúng 3
Bình luận (0)
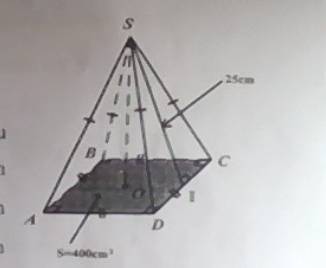
4: Độ dài cạnh đáy là \(\sqrt{400}=20\left(cm\right)\)
Chu vi đáy là 20*4=80(cm)
Diện tích xung quanh là \(80\cdot25=2000\left(cm^2\right)\)
Diện tích toàn phần là:
\(2000+400=2400\left(cm^2\right)\)
Đúng 1
Bình luận (0)
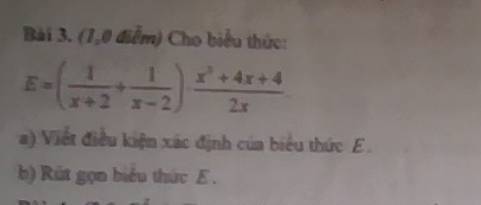

hình bài 4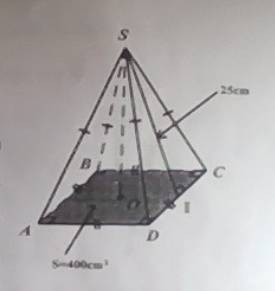
\(3,\\ a,đkxđ:\left\{{}\begin{matrix}x+2\ne0\\x-2\ne0\\2x\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne-2\\x\ne2\\x\ne0\end{matrix}\right.\)
\(b,E=\left(\dfrac{1}{x+2}+\dfrac{1}{x-2}\right)\cdot\dfrac{x^2+4x+4}{2x}\\ =\left(\dfrac{x-2}{\left(x+2\right)\left(x-2\right)}+\dfrac{x+2}{\left(x-2\right)\left(x+2\right)}\right)\cdot\dfrac{\left(x+2\right)^2}{2x}\\ =\dfrac{x-2+x+2}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{\left(x+2\right)^2}{2x}\\ =\dfrac{2x}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{\left(x+2\right)^2}{2x}\\ =\dfrac{x+2}{x-2}\)
Đúng 4
Bình luận (0)
Bài 4:
Đáy của hình chóp tứ giác đều S.ABCD là hình vuông
=> Cạnh đáy hình chóp tứ giác đều S.ABCD là: 400 : 2 = 20 (cm)
Diện tích xung quanh của hình chóp tứ giác đều S.ABCD là:
Sxq = \(\dfrac{1}{2}\).C.d = \(\dfrac{1}{2}\) . 20.4.25 = 1000 (\(cm^2\))
Diện tích toàn phần của hình chóp tứ giác đều S.ABCD là:
Stp = Sxq + S đáy = 1000 + 400 = 1400 (cm2 )
Đúng 1
Bình luận (0)