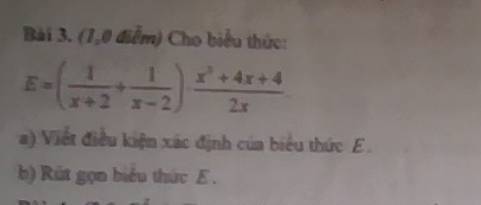\(3,\\ a,đkxđ:\left\{{}\begin{matrix}x+2\ne0\\x-2\ne0\\2x\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne-2\\x\ne2\\x\ne0\end{matrix}\right.\)
\(b,E=\left(\dfrac{1}{x+2}+\dfrac{1}{x-2}\right)\cdot\dfrac{x^2+4x+4}{2x}\\ =\left(\dfrac{x-2}{\left(x+2\right)\left(x-2\right)}+\dfrac{x+2}{\left(x-2\right)\left(x+2\right)}\right)\cdot\dfrac{\left(x+2\right)^2}{2x}\\ =\dfrac{x-2+x+2}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{\left(x+2\right)^2}{2x}\\ =\dfrac{2x}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{\left(x+2\right)^2}{2x}\\ =\dfrac{x+2}{x-2}\)
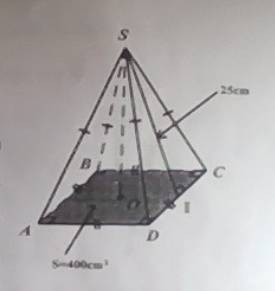
Bài 4:
Đáy của hình chóp tứ giác đều S.ABCD là hình vuông
=> Cạnh đáy hình chóp tứ giác đều S.ABCD là: 400 : 2 = 20 (cm)
Diện tích xung quanh của hình chóp tứ giác đều S.ABCD là:
Sxq = \(\dfrac{1}{2}\).C.d = \(\dfrac{1}{2}\) . 20.4.25 = 1000 (\(cm^2\))
Diện tích toàn phần của hình chóp tứ giác đều S.ABCD là:
Stp = Sxq + S đáy = 1000 + 400 = 1400 (cm2 )