Đố :
Cho ba điểm A, D, K trên giấy kẻ ô vuông (h.32).
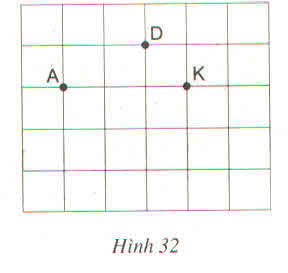
Hãy tìm điểm thứ tư M là giao điểm của các dòng kẻ sao cho nó cùng với ba điểm đã cho là bốn đỉnh của một hình thang cân.
Đố :
Cho ba điểm A, D, K trên giấy kẻ ô vuông (h.32).

Hãy tìm điểm thứ tư M là giao điểm của các dòng kẻ sao cho nó cùng với ba điểm đã cho là bốn đỉnh của một hình thang cân.
Hình thang cân ABCD có AB // CD, AB < CD. Kẻ các đường cao AH, BK. Chứng minh rằng DH = CK ?
Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy theo thứ tự các điểm D và E sao cho AD = AE.
a) Chứng minh rằng BDEC là hình thang cân
b) Tính các góc của hình thang cân đó, biết rằng \(\widehat{A}=50^0\)
Hình vẽ:

a)Xét \(\Delta ADE\) có:AD=AE(gt)
\(\Rightarrow\Delta ADE\) cân tại A
\(\Rightarrow\widehat{AED}=\dfrac{180^0-\widehat{A}}{2}\) (1)
Ta lại có:\(\Delta ABC\) cân tại A
\(\Rightarrow\widehat{ACB}=\dfrac{180^o-\widehat{A}}{2}\) (2)
Từ (1) và (2) \(\Rightarrow\widehat{AED}=\widehat{ACB}\)
\(\Rightarrow\) DE song song với BC
Xét tứ giác DEBC có:
DE song song với BC
\(\widehat{ABC}=\widehat{ACB}\) ( 2 góc đáy của tam giác ABC cân tại A)
\(\Rightarrow\) BDEC là hình thang cân
\(\Rightarrow\widehat{BDE}=\widehat{CED}\)
b) Theo câu a có:\(\widehat{ACB}=\dfrac{180^o-\widehat{A}}{2}=\dfrac{180^o-50^o}{2}=60^0\)
mà \(\widehat{ABC}=\widehat{ACB}\) ( câu a) nên \(\widehat{ABC}=60^o\)
Vì DE song song với BC\(\Rightarrow\) góc DEC+ góc BCE=180o
=>góc DEC+60o =180o
=>góc DEC=120o mà \(\widehat{BDE}=\widehat{CED}\)
=>BDE=120o
Trả lời bởi Đạt Trần
Chứng minh định lí : "Hình thang có hai đường chéo bằng nhau là hình thang cân" qua bài toán sau :
Cho hình thang ABCD (AB // CD) có AC = BD. Qua B kẻ đường thẳng song song với AC, cắt đường thẳng DC tại E. Chứng minh rằng :
a) \(\Delta BDE\) là tam giác cân
b) \(\Delta ACD=\Delta BDC\)
c) Hình thang ABCD là hình thang cân
a) Hình thang ABEC (AB // CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau:
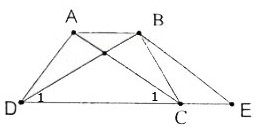
AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó tam giác BDE cân.
b) Ta có AC // BE suy ra  =
=  (3)
(3)
∆BDE cân tại B (câu a) nên  =
=  (4)
(4)
Từ (3) và (4) suy ra  =
= 
Xét ∆ACD và ∆BCD có AC = BD (gt)
 =
=  (cmt)
(cmt)
CD cạnh chung
Nên ∆ACD = ∆BDC (c.g.c)
c) ∆ACD = ∆BDC (câu b)
Suy ra 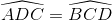
Hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.
Trả lời bởi Tuyen CaoCho tam giác ABC cân tại A, các đường phân giác BD, CE ( \(D\in AC,E\in AB\) )
Chứng minh rằng BEDC là hình thang có đáy nhỏ bằng cạnh bên.
Đố :
Trong các tứ giác ABCD và EFGH trên giấy kẻ ô vuông (h.31) tứ giác nào là hình thang cân ? Vì sao ?
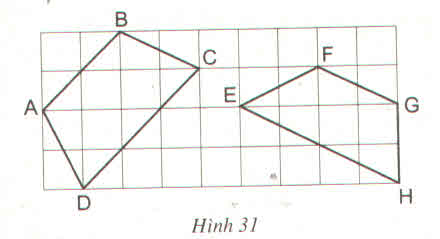
Bài giải:
Để xét xem tứ giác nào là hình thang cân ta dùng tính chất
"Trong hình thang cân hai cạnh bên bằng nhau"
Tứ giác ABCD là hình thang cân vì có AD = BC.
Tứ giác EFGH không là hình thang cân vì EF > GH.
Trả lời bởi Tuyết Nhi MelodyCho hình thang cân ABCD (AB // CD, AB < CD). Kẻ các đường cao AE, BF của hình thang. Chứng minh rằng DE = CF ?
Bài giải:
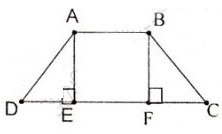
Xét hai tam giác vuông AED và BFC
Ta có: AD = BC (gt)
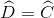 (gt)
(gt)
Nên ∆AED = ∆BFC (cạnh huyền - góc nhọn)
Suy ra: DE = CF
Trả lời bởi Tuyết Nhi MelodyTính độ dài các cạnh của hình thang cân ABCD trên giấy kẻ ô vuông (H.30, độ dài của cạnh ô vuông là 1cm)
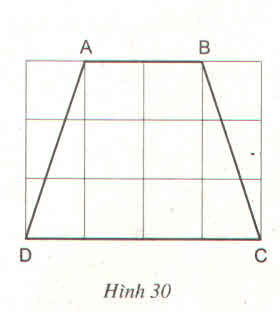
Bài giải:
Theo hình vẽ, ta có: AB = 2cm, CD = 4cm
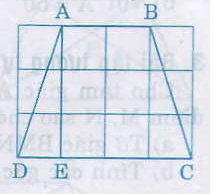
Trong tam giác vuông AED, áp dụng định lý Pitago ta được:
AD2 = AE2 + ED2
= 32 + 12 =10
Suy ra AD = cm
Vậy AB = 2cm, CD = 4cm, AD = BC = cm
Trả lời bởi Tuyết Nhi MelodyCho hình thang cân ABCD (AB // CD), E là giao điểm của hai đường chéo. Chứng minh rằng EA = EB, EC = ED ?
Bài giải:
Do ABCD là hình thang cân nên AD = BC, AC = BC,
Xét hai tam giác ADC và BCD, ta có: 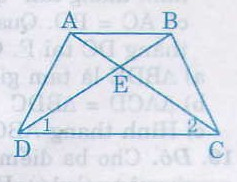
AD = BC (gt)
AC = BD (gt)
DC chung
Nên ∆ADC = ∆BCD (c.c.c)
Suy ra
Do đó tam giác ECD cân tại E, nên EC = ED
Ta lại có: AC = BD suy ra EA = EB
Chú ý: Ngoài cách chứng minh ∆ADC = ∆BCD (c.c.c) ta còn có thể chứng minh ∆ADC = ∆BCD (c.g.c) như sau:
AD = BC, , DC là cạnh chung.
Trả lời bởi Tuyết Nhi MelodyHình thang ABCD (AB//CD) có \(\widehat{ACD}=\widehat{BDC}\). Chứng minh rằng ABCD là hình thang cân ?
Bài giải:
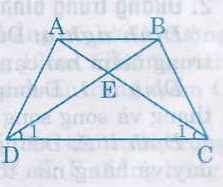
Gọi E là giao điểm của AC và BD.
∆ECD có \(\widehat{C_1}=\widehat{D}\) (do \(\widehat{ACD}=\widehat{BDC}\)) nên là tam giác cân.
Suy ra EC = ED (1)
Tương tự EA = EB (2)
Từ (1) và (2) suy ra AC = BD
Hình thang ABCD có hai đường chéo bằng nhau nên là hình thang cân.
Bài giải:
Có thể tìm được hai điểm M là giao điểm của các dòng kẻ sao cho nó cùng với ba điểm đã cho A, D, K là bốn đỉnh của một hình thang cân. Đó là hình thang AKDM1 (với AK là đáy) và hình thang ADKM2 (với DK là đáy).
Trả lời bởi Hiiiii~