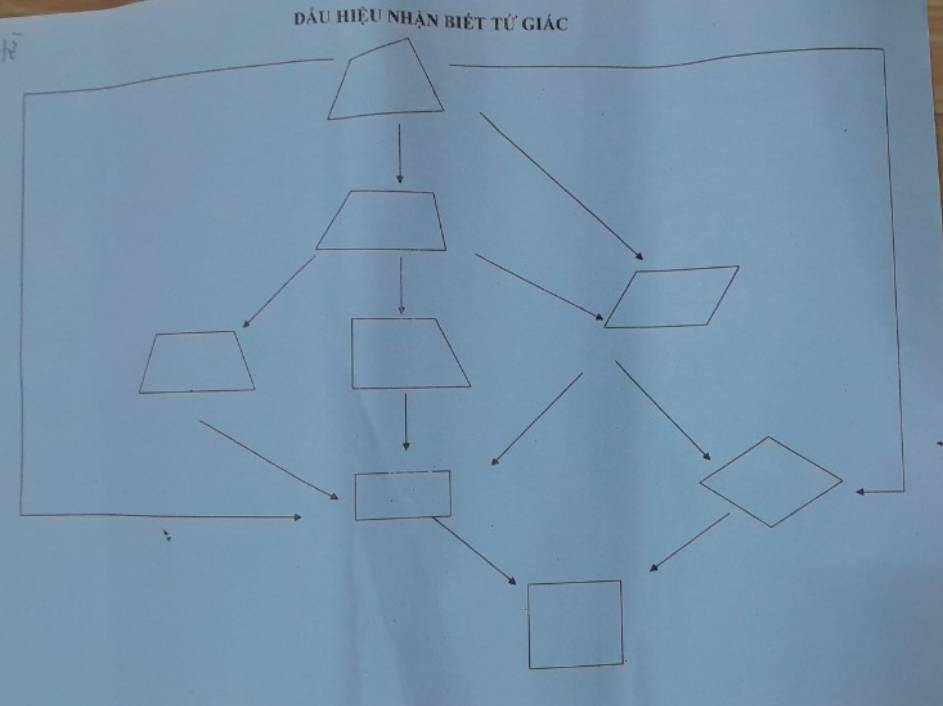
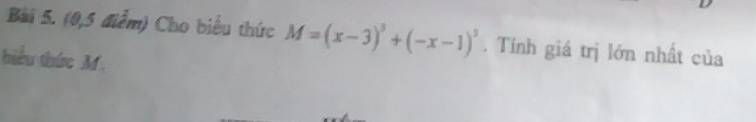
Bài 3: Hình thang cân

5:

\(M=\left(x-3\right)^3+\left(-x-1\right)^3\)

\(=x^3-9x^2+27x-27-x^3-3x^2-3x-1\)

\(=-12x^2+24x-28\)

\(=-12\left(x^2-2x+\dfrac{7}{3}\right)\)

\(=-12\left(x^2-2x+1+\dfrac{4}{3}\right)\)

\(=-12\left(x-1\right)^2-16< =-16\)

Dấu = xảy ra khi x=1

Cậu tham khảo nha :>

Bài 1: 

Diện tích đáy của hình chóp đều là:

\(V=\dfrac{1}{3}Sh\Rightarrow S=\dfrac{3V}{h}=\dfrac{3\cdot125}{15}=25\left(cm^2\right)\)

Cạnh đáy của tứ giác là:

\(a=\sqrt{25}=5\left(cm\right)\)

Chu vi đáy của chóp tứ giác đều là:

\(C=4a=4\cdot5=20\left(cm\right)\)

1.

Diện tích đáy của hình chóp tứ giác đều là:

\(\left(125:15\right):\dfrac{1}{3}=25\left(cm^2\right)\)

Độ dài cạnh đáy của hình chóp tứ giác đều là:

\(\sqrt{25}=5\left(cm\right)\)

Chu vi đáy của hình chóp tứ giác đều là:

\(5\cdot4=20\left(cm\right)\)

Vậy: ...

2.

Diện tích xung quanh của khối bê tông là:

\(\dfrac{1}{2}\cdot\left(2\cdot3\right)\cdot3=9\left(m^2\right)\)

Số tiền cần phải trả khi sơn cả ba mặt xung quanh là:

\(9\cdot30000=270000\left(đồng\right)\)

Vậy: ...

\(Toru\)

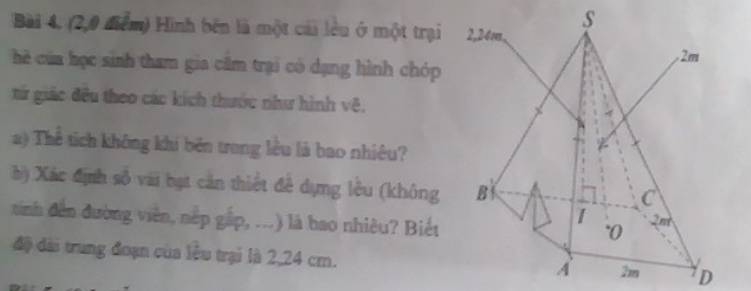
Bài 2: 

Nữa chu vi đáy của hình chóp là:

\(p=\dfrac{3\cdot2}{2}=3\left(m\right)\)

Diện tích xung quanh của hình chóp đều:

\(S_{xq}=p\cdot d=3\cdot3=9\left(m^2\right)\)

Số tiền cần trả khi sơn 3 mặt của hình chóp là:

\(T=S_{xq}\cdot30000=9\cdot30000=270000\left(đ\right)\)

\(\widehat{A}=\widehat{B}=180^0-\widehat{C}=140^0\)

=>\(\widehat{C}=180^0-140^0=40^0\) và \(\widehat{A}=\widehat{B}=140^0\)

\(\widehat{C}=\widehat{D}=40^0\)