Bài 1: Góc ở tâm. Số đo cung

a: Xét (O) có

ΔABC nội tiếp

BC là đường kính

Do đó: ΔABC vuông tại A

Gọi N là trung điểm của AH

=>N là tâm đường tròn đường kính AH

Xét (N) có

ΔAEH nội tiếp

AH là đường kính

Do đó: ΔAEH vuông tại E

=>HE\(\perp\)AB tại E

Xét (N) có

ΔAFH nội tiếp

AH là đường kính

Do đó: ΔAFH vuông tại F

=>HF\(\perp\)AC tại F

Xét tứ giác AEHF có \(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)

nên AEHF là hình chữ nhật

b: Ta có: AEHF là hình chữ nhật

=>\(\widehat{AEF}=\widehat{AHF}\)

mà \(\widehat{AHF}=\widehat{ACB}\left(=90^0-\widehat{HAC}\right)\)

nên \(\widehat{AEF}=\widehat{ACB}\)

mà \(\widehat{AEF}+\widehat{BEF}=180^0\)(hai góc kề bù)

nên \(\widehat{BEF}+\widehat{BCF}=180^0\)

=>BEFC là tứ giác nội tiếp

c: Gọi Ax là tiếp tuyến của (O) tại A

Xét (O) có

\(\widehat{xAC}\) là góc tạo bởi tiếp tuyến Ax và dây cung AC

\(\widehat{ABC}\) là góc nội tiếp chắn cung AC

Do đó: \(\widehat{xAC}=\widehat{ABC}\)

mà \(\widehat{ABC}=\widehat{AFE}\left(=180^0-\widehat{EFC}\right)\)

nên \(\widehat{xAC}=\widehat{AFE}\)

mà hai góc này là hai góc ở vị trí so le trong

nên FE//Ax

Ta có: FE//Ax

OA\(\perp\)Ax

Do đó: OA\(\perp\)FE

help me

1: Xét (O) có

ΔCND nội tiếp

CD là đường kính

Do đó: ΔCND vuông tại N

=>ND\(\perp\)CM tại N

Xét tứ giác CNEK có \(\widehat{CNE}+\widehat{CKE}=90^0+90^0=180^0\)

nên CNEK là tứ giác nội tiếp

Xét tứ giác MNKD có \(\widehat{MND}=\widehat{MKD}=90^0\)

nên MNKD là tứ giác nội tiếp

2: Xét ΔMNE vuông tại N và ΔMKC vuông tại K có

\(\widehat{NME}\) chung

Do đó: ΔMNE~ΔMKC

=>\(\dfrac{MN}{MK}=\dfrac{ME}{MC}\)

=>\(MN\cdot MC=ME\cdot MK\)

3: Xét (O) có

ΔCHD nội tiếp

CD là đường kính

Do đó: ΔCHD vuông tại H

=>CH\(\perp\)MD

Xét ΔMCD có

CH,DN,MK là các đường cao

DN cắt MK tại E

Do đó: C,E,H thẳng hàng

help me please

giúp mk vs ạ thanks trước

Xét ΔOBA vuông tại A có \(cosBOA=\dfrac{OA}{OB}=\dfrac{1}{2}\)

nên \(\widehat{BOA}=60^0\)

Xét ΔOAC có OA=OC và \(\widehat{AOC}=60^0\)

nên ΔOAC đều

=>\(sđ\stackrel\frown{AC}\left(nhỏ\right)=60^0\)

Số đo cung AC lớn là: 

\(360-60=300^0\)

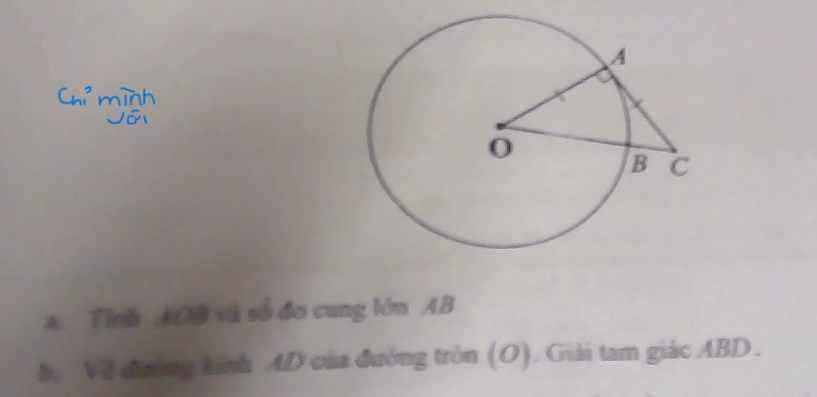
a: Xét ΔAOC có AO=AC và \(\widehat{OAC}=90^0\)

nên ΔAOC vuông cân tại A

=>\(\widehat{AOB}=\widehat{AOC}=45^0\)

Xét (O) có

\(\widehat{AOB}\) là góc ở tâm chắn cung AB nhỏ

=>\(sđ\stackrel\frown{AB}\left(lớn\right)=360^0-\widehat{AOB}=315^0\)

b: Xét (O) có

ΔABD nội tiếp

AD là đường kính

Do đó: ΔABD vuông tại B

Xét ΔOAB có \(cosAOB=\dfrac{OA^2+OB^2-AB^2}{2\cdot OA\cdot OB}\)

=>\(\dfrac{R^2+R^2-AB^2}{2\cdot R\cdot R}=cos45=\dfrac{\sqrt{2}}{2}\)

=>\(2R^2-AB^2=R^2\cdot\sqrt{2}\)

=>\(AB^2=R^2\left(2-\sqrt{2}\right)\)

=>\(AB=R\sqrt{2-\sqrt{2}}\)

ΔABD vuông tại B

=>\(BA^2+BD^2=AD^2\)

=>\(BD^2=AD^2-AB^2=4R^2-R^2\left(2-\sqrt{2}\right)=R^2\left(2+\sqrt{2}\right)\)

=>\(BD=R\sqrt{2+\sqrt{2}}\)

Xét ΔABD vuông tại B có \(cosBAD=\dfrac{AB}{AD}=\dfrac{R\sqrt{2-\sqrt{2}}}{2R}=\dfrac{\sqrt{2-\sqrt{2}}}{2}\)

=>\(\widehat{BAD}=67,5^0\)

ΔABD vuông tại B

=>\(\widehat{BAD}+\widehat{BDA}=90^0\)

=>\(\widehat{BDA}=90^0-67,5^0=22,5^0\)

Đầu tiên bạn vẽ một đường tròn bất kì

sau đó bạn đo bán kính của nó và nhân với \(\dfrac{\sqrt{3}}{2}\)

Và vẽ đường tròn còn lại với tâm là đường tròn thứ nhất, bán kính là kết quả của phép tính trên

2:

a: Xét ΔOAB có OA=OB=AB

nên ΔOAB đều

=>\(\widehat{AOB}=60^0\)

=>Số đo cung nhỏ AB là 60⁰

Số đo cung lớn AB là 360-60=300⁰

b: ΔOAB đều

mà OI là đường trung tuyến

nên \(OI=AB\cdot\dfrac{\sqrt{3}}{2}=\dfrac{R\sqrt{3}}{2}\)

c: Xét (O) có

MA,MB là tiếp tuyến

=>MA=MB

=>M nằm trên đường trung trực của AB(1)

ΔOAB cân tại O

mà OI là đường trung tuyến

nên OI là đường trung trực của AB(2)

Từ (1),(2) suy ra O,I,M thẳng hàng

a: góc AOC; góc BOD; góc AOD; góc BOC

b: góc COB=góc AOD=60 độ

=>sđ cung BC=60 đọ

góc AOC=180-60=120 độ

=>sđ cung AC=120 độ

c: sđ cung AC>sđ cung AD

=>AD>AC

a: Xét ΔOAM vuông tại A có cosAOM=OA/OM=1/2

nên góc AOM=60 độ

=>góc AOB=60 độ

=>sđ cung AB=60 độ

b: Xét (O) có

MA,MC là tiếp tuyến

nên MA=MC

mà OA=OC

nên OM là trung trực của AC

=>OM vuông góc với AC

c: Xét ΔOAB có OA=OB và góc AOB=60 độ

nên ΔOAB đều

mà AH là đườg cao

nên H là trung điểm của OB

=>HO=HB

Vì MO là trung trực của AC

nên MO vuông góc AC tại H và H là trung điểm của AC

HA*HC=HA^2

HO*HM=HA^2

=>HA*HC=HO*HM

=>HA*HC=HB*HM

d: Xét ΔOBC có OB=OC và góc BOC=60 độ

nên ΔBCO đều

=>OB=OC=BC=OA=AB

=>OA=AB=BC=OC

=>OABC là hình thoi