Lời giải:
a.
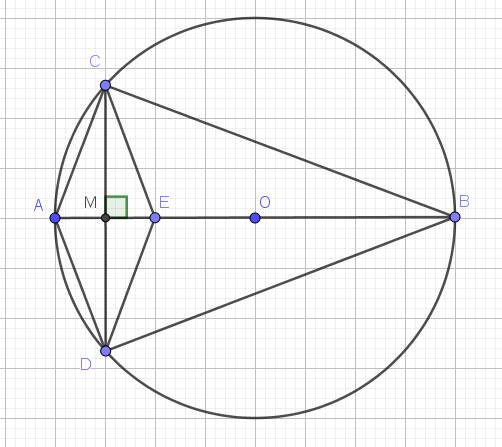
Ta thấy $OC=OD=R$ nên tam giác $OCD$ cân tại $O$
$\Rightarrow$ đường cao $OM$ đồng thời là trung tuyến
$\Rightarrow M$ là trung điểm của $CD$
Tứ giác $ACED$ có 2 đường chéo $AE, CD$ cắt nhau tại trung điểm $M$ của mỗi đường nên là hình bình hành.
Mà $AE\perp CD$ nên $ACED$ là hình thoi.
b. Vì $ACED$ là hình thoi nên $AC\parallel DE(1)$
Mà $\widehat{ACB}=90^0$ (góc nội tiếp chắn nửa đường tròn - AB)
$\Rightarrow AC\perp CB(2)$
Từ $(1); (2)\Rightarrow DE\perp CB$
Mà $BE\perp CD$ nên $E$ là trực tâm của $BCD$.
Đúng 2
Bình luận (0)