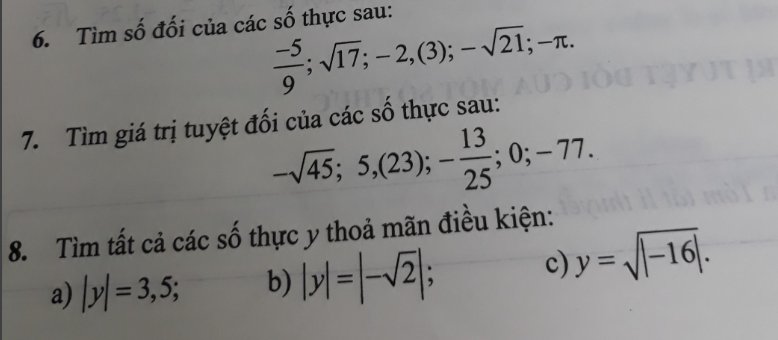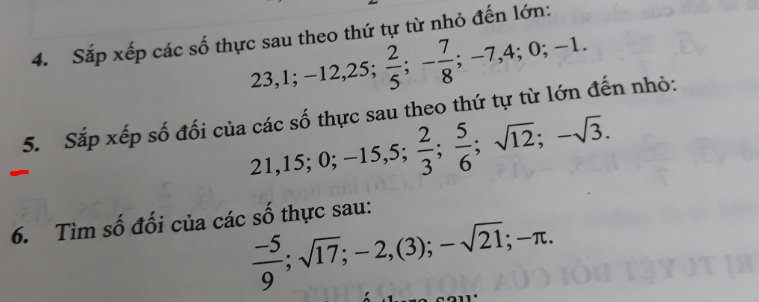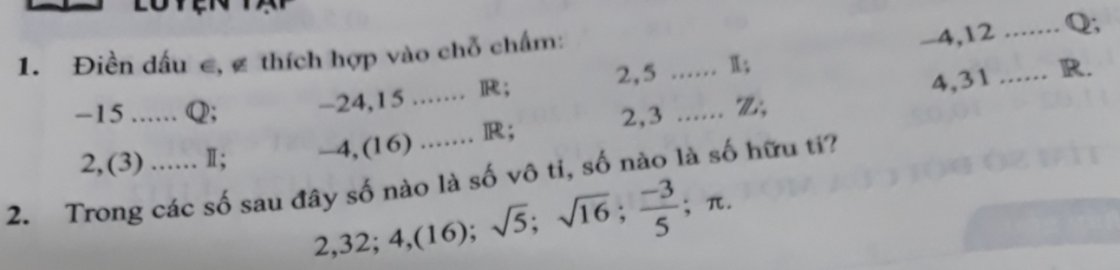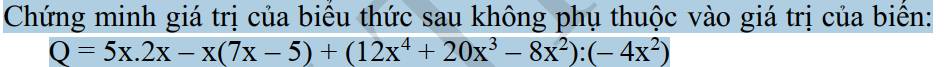Bài 12: Số thực

\(Q=5x\cdot2x-x\left(7x-5\right)+\left(12x^4+20x^3-8x^2\right):-4x^2\)

\(Q=10x^2-7x^2+5x+\dfrac{4x^2\left(3x^2+5x-2\right)}{-4x^2}\)

\(Q=3x^2+5x-\left(3x^2+5x-2\right)\)

\(Q=3x^2+5x-3x^2-5x+2\)

\(Q=2\)

Vậy giá trị của Q không phụ thuộc vào biến x

11: Sẽ là số vô tỉ

12: Sẽ là số vô tỉ

10: 

8:

a: |y|=3,5

=>y=3,5 hoặc y=-3,5

b: |y|=|-căn 2|

=>|y|=căn 2

=>y=căn 2 hoặc y=-căn 2

c: y=căn |-16|

=>y=căn 16=4

7:

\(\left|-\sqrt{45}\right|=\sqrt{45};\left|5,\left(23\right)\right|=5,\left(23\right)\)

\(\left|-\dfrac{13}{25}\right|=\dfrac{13}{25};\left|0\right|=0;\left|-77\right|=77\)

`@` `\text {Ans}`

`\downarrow`

`6.`

`-` Số đối của `1` số là số mà khi cộng lại tổng của `2` số đó bằng `0`

`=>`

Số đối của số `-5/9` là `5/9`

Số đối của `\sqrt {17}` là `- \sqrt {17}`

Số đối của `-2(3)` là `2(3)`

Số đối của `-\sqrt {21}` là `\sqrt {21}`

Số đối của \(-\pi\) là \(\pi\)

`7.`

`| - \sqrt {45}| = \sqrt {45}`

`| 5,(23) | = 5,(23)`

`| -13/25| = 13/25`

`| 0 |=0`

`| -77| = 77`

`8.`

`a)`

`|y| = 3,5`

`=> y \in {3,5 ; -3,5}`

`b)`

`|y| = | -\sqrt {2}|`

`=> |y| = \sqrt {2}`

`=> y \in {2; -2}`

`c)`

`y = \sqrt {|-16|}`

`=> y = \sqrt {16}`

`=> y = 4`

`@` `\text {Duynamlvhg}`

11: Sẽ là số vô tỉ

12: Sẽ là số vô tỉ

10: 

5:

\(21,15>\sqrt{12}>\dfrac{5}{6}>\dfrac{2}{3}>0>-\sqrt{3}>-15,5\)

4: 

\(-12,25< -7,4< -1< -\dfrac{7}{8}< 0< \dfrac{2}{5}< 23,1\)

21,15 ; \(\sqrt{12}\); \(\dfrac{5}{6};\dfrac{2}{3}\);0,\(-\sqrt{3}\);-15,5

2:

Số hữu tỉ: 2,32; 4,(16), căn 16; -3/5

Số vô tỉ: \(\sqrt{5};\Pi\)

1:

\(-15\in Q;-24,15\in R;2,5\notin I;-4,12\in Q\)

\(2,\left(3\right)\notin I;-4,\left(16\right)\in R;2,3\notin Z;4,31\in R\)

làm như kiểu này nè... xem thêm

a: góc C=90-60=30 độ<góc B

=>AB<AC

=>HB<HC

b: Xet ΔAHB vuông tại H và ΔAHM vuông tại H có

AH chung

HB=HM

=>ΔAHB=ΔAHM

=>AB=AM

mà góc B=60 độ

nên ΔAMB đều

#\(N\)

\(\left|2x+4\right|\ge0\) \(\left(\forall x\right)\)

\(\left(y+2\right)^2\ge0\left(\forall y\right)\)

`=> |2x+4|+(y+2)^2`\(\ge0\) (với mọi x, y)

`=>`\(\left\{{}\begin{matrix}\left|2x+4\right|=0\\\left(y+2\right)^2=0\end{matrix}\right.\)

`=>` \(\left\{{}\begin{matrix}2x+4=0\\y+2=0\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}2x=0-4\\y=0-2\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}2x=-4\\y=-2\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x=-4\div2\\y=-2\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x=-2\\y=-2\end{matrix}\right.\)

vậy, `x=-2, y=-2`

=>2x+4=0 và y+2=0

=>x=-2 và y=-2