Bài 1: Tổng ba góc của một tam giác

a) Xét \(\Delta ABC\) có:

\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\) (Định lý tổng ba góc trong một tam giác)

⇔ \(\widehat{A}+65^o+65^o=180^o\)

⇔\(\widehat{A}+130^o=180^o\)

⇔\(\widehat{A}=180^o-130^{o^{ }}\)

⇔\(\widehat{A}=50^o\)

Hay \(\widehat{BAC}=50^o\)

b) Vì \(Am\) // BC (gt)

⇔\(\widehat{CAm}=\widehat{C}\) (vì 2 góc so le trong)

mà \(\widehat{C}=65^o\) (gt)

⇔\(\widehat{CAm}=65^o\)

Vì AC nằm giữa tia AB và Am

⇔\(\widehat{BAC}+\widehat{CAm}=\widehat{BAm}\)

⇔\(50^o+65^o=\widehat{BAm}\)

⇔\(\widehat{BAm}=115^o\)

Ta có \(\widehat{BAm}+\widehat{nAm}=180^o\) (vì 2 góc kề bù)

⇔ \(115^o+\widehat{nAm}=180^o\)

⇔\(\widehat{nAm}=180^o-115^o\)

⇔\(\widehat{nAm}=65^o\)

mà \(\widehat{CAm}=65^o\) (cmt)

⇔\(\widehat{nAm}=\widehat{CAm}=65^o\)

⇔Am là tia phân giác của \(\widehat{nAC}\) (đpcm)

góc DFE=180-60-70=50 độ

=>góc DFK=góc EFK=50/2=25 độ

góc DKF=góc KEF+góc KFE=70+25=95 độ

góc EKF=180-95=85 độ

`@\hat{B}-\hat{C}=30^o =>\hat{B}=30^o +\hat{C}`

`@2\hat{C}-\hat{A}=100^o =>\hat{A}=2\hat{C}-100^o`

Xét `\triangle ABC` có: `\hat{A}+\hat{B}+\hat{C}=180^o`

  `=>2\hat{C}-100^o +30^o +\hat{C}+\hat{C}=180^o`

  `=>4\hat{C}=250^o`

  `=>\hat{C}=62,5^o`

`=>\hat{B}=30^o +62,5^o =92,5^o`

 và `\hat{A}=2.62,5^o -100^o =25^o`

Lời giải:

Gọi độ đo góc $\widehat{A}, \widehat{B}, \widehat{C}$ lần lượt là $a,b,c$. Ta có:

$b-c=30^0(1)$

$2c-a=100^0(2)$

$a+b+c=180^0(3)$

Lấy $(2)-(1)$ có:$3c-(a+b)=70^0$

$\Rightarrow 4c-(a+b+c)=70^0$

$\Rightarrow 4c-180^0=70^0$

$\Rightarrow c=62,5^0$

$a=2c-100^0=2.62,5^0-100^0=25^0$

$b=30^0+c=30^0+62,5^0=92,5^0$

Sửa đề: Trên tia Ox lấy B,D, trên tia Oy lấy C,E sao cho OD=OE; OB=OC

a: Xét ΔOCD và ΔOBE có

OC=OB

góc O chung

OD=OE

=>ΔOCD=ΔOBE

b: Xét ΔABD và ΔACE có

góc ABD=góc ACE

BD=CE
góc ADB=góc AEC

=>ΔABD=ΔACE
=>AB=AC

Xét ΔAOB và ΔAOC có

AO chung

OB=OC

AB=AC

=>ΔAOB=ΔAOC

c: OB=OC

AB=AC

=>OAlà trung trực của BC

=>OA vuông góc với BC

a: góc DIC=180 độ-góc BIC

=180 độ-180 độ+1/2(góc ABC+góc ACB)

=1/2(180 độ-góc BAC)

=90 độ-1/2góc BAC<90 độ

=>góc DIC nhọn

b: góc BIC=180-60=120 độ

=>góc IBC+góc ICB=60độ

=>góc ABC+góc ACB=120 độ

=>góc A=60 độ

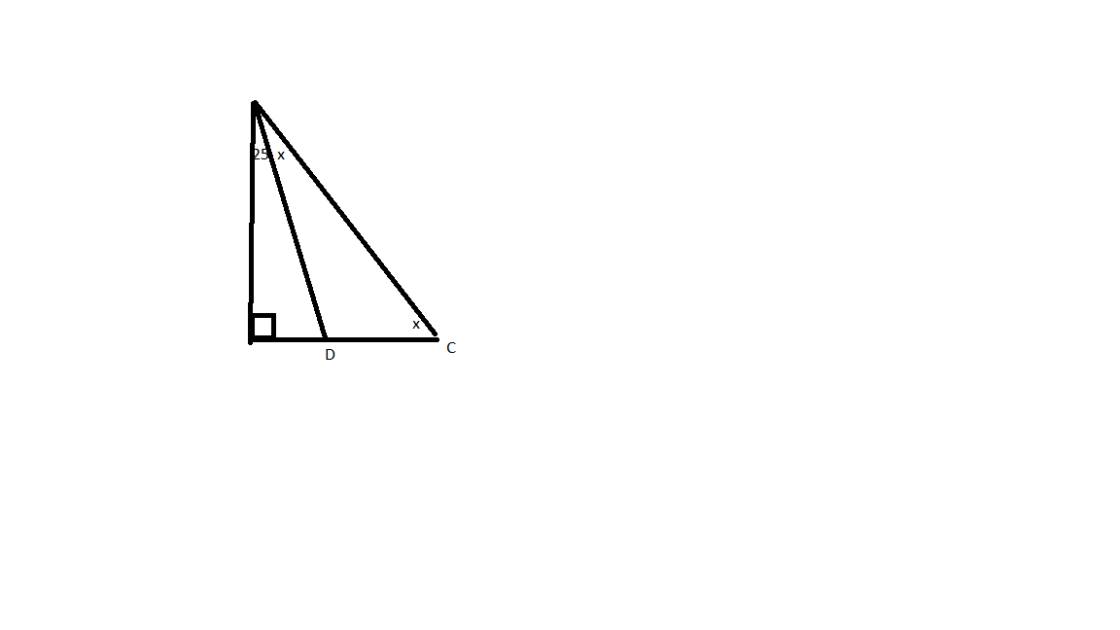
z đâu bạn nhỉ :)? có 2 x lận

a. Ta có:

 \(\left\{{}\begin{matrix}\widehat{A}=\widehat{B}\\\widehat{B}=2\widehat{C}\end{matrix}\right.\)

 \(\Rightarrow\widehat{A}+\widehat{B}=4\widehat{C}\)  

Xét tam giác ABC có:

\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\) (định lí tổng 3 góc trong 1 tam giác)

Mà \(\widehat{A}+\widehat{B}=4\widehat{C}\)

\(\Rightarrow4\widehat{C}+\widehat{C}=180^o\)

\(5\widehat{C}=180^o\)

\(\widehat{C}=180^o:5\)

\(\widehat{C}=36^o\)

\(\Rightarrow\left\{{}\begin{matrix}\widehat{B}=2\widehat{C}=2.36^o=72^o\\\widehat{A}=\widehat{B}=72^o\end{matrix}\right.\)

b. Ta có: \(\widehat{A}=\widehat{B}\)

\(\Rightarrow\) Tam giác ABC cân tại \(C\)

a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{a}{2}=\dfrac{b}{7}=\dfrac{c}{1}=\dfrac{a+b+c}{2+7+1}=\dfrac{180}{10}=18\)

=>a=36; b=126; c=18

b: góc A+góc C=180-75=105 độ

=>góc A=3/5*105=63 độ

góc C=105-63=42 độ

a: góc D=góc A=60 độ

góc B=góc E=75 độ

góc F=180-60-75=45 độ

b: \(C_{DEF}=10+12+8=30\left(cm\right)\)