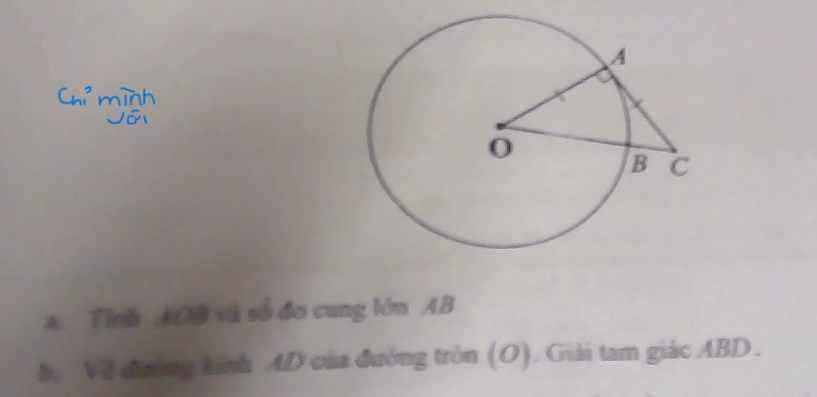
a: Xét ΔAOC có AO=AC và \(\widehat{OAC}=90^0\)
nên ΔAOC vuông cân tại A
=>\(\widehat{AOB}=\widehat{AOC}=45^0\)
Xét (O) có
\(\widehat{AOB}\) là góc ở tâm chắn cung AB nhỏ
=>\(sđ\stackrel\frown{AB}\left(lớn\right)=360^0-\widehat{AOB}=315^0\)
b: Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
Xét ΔOAB có \(cosAOB=\dfrac{OA^2+OB^2-AB^2}{2\cdot OA\cdot OB}\)
=>\(\dfrac{R^2+R^2-AB^2}{2\cdot R\cdot R}=cos45=\dfrac{\sqrt{2}}{2}\)
=>\(2R^2-AB^2=R^2\cdot\sqrt{2}\)
=>\(AB^2=R^2\left(2-\sqrt{2}\right)\)
=>\(AB=R\sqrt{2-\sqrt{2}}\)
ΔABD vuông tại B
=>\(BA^2+BD^2=AD^2\)
=>\(BD^2=AD^2-AB^2=4R^2-R^2\left(2-\sqrt{2}\right)=R^2\left(2+\sqrt{2}\right)\)
=>\(BD=R\sqrt{2+\sqrt{2}}\)
Xét ΔABD vuông tại B có \(cosBAD=\dfrac{AB}{AD}=\dfrac{R\sqrt{2-\sqrt{2}}}{2R}=\dfrac{\sqrt{2-\sqrt{2}}}{2}\)
=>\(\widehat{BAD}=67,5^0\)
ΔABD vuông tại B
=>\(\widehat{BAD}+\widehat{BDA}=90^0\)
=>\(\widehat{BDA}=90^0-67,5^0=22,5^0\)