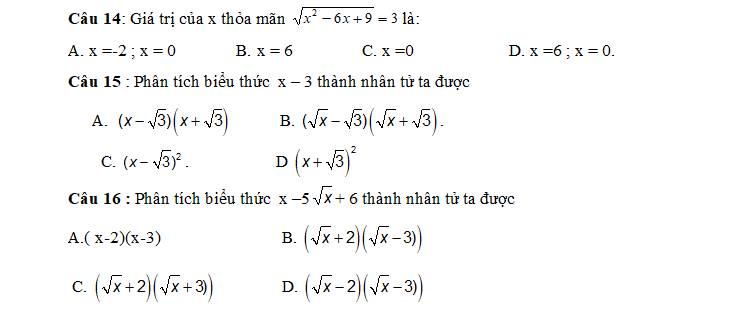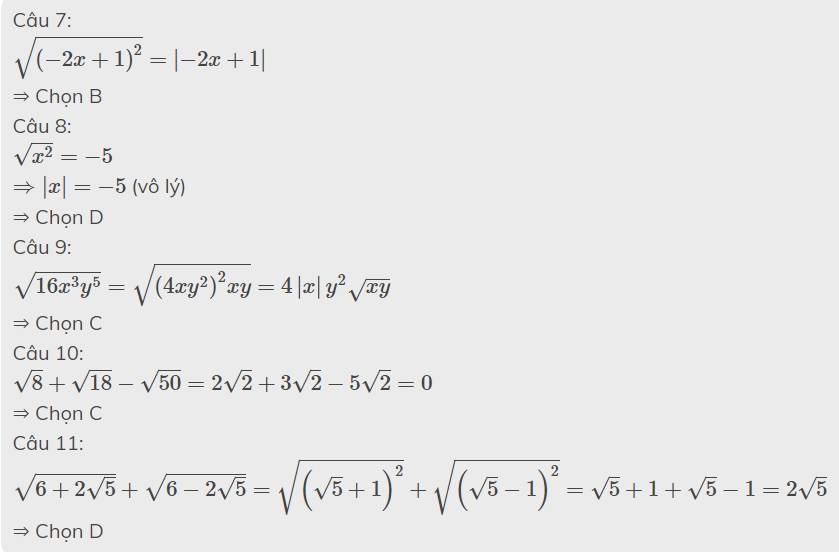b) (sqrt(10) - sqrt(5))/(sqrt(2) - 1) - (3sqrt(5) + 5)/(sqrt(5) + 3) + 2/(sqrt(2))
Bài 1: Căn bậc hai
\(=\dfrac{\sqrt{5}\left(\sqrt{2}-1\right)}{\sqrt{2}-1}-\dfrac{\sqrt{5}\left(3+\sqrt{5}\right)}{3+\sqrt{5}}+\sqrt{2}\)
\(=\sqrt{5}-\sqrt{5}+\sqrt{2}\)
\(=\sqrt{2}\)
Đúng 2
Bình luận (0)
Câu 14:
\(-x^2\sqrt{\dfrac{y}{x}}=-\sqrt{x^4\cdot\dfrac{y}{x}}=-\sqrt{x^3y}=-x\sqrt{xy}\)
⇒ Chọn A
Câu 15:
\(\sqrt{2x+1}=3x-1\)
\(\Leftrightarrow2x+1=9x^2-6x+1\)
\(\Leftrightarrow9x^2-8x=0\)
\(\Leftrightarrow x\left(9x-8\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{8}{9}\end{matrix}\right.\)
⇒ Chọn A
Câu 17:
\(\sqrt{\dfrac{a}{b}}+\dfrac{a}{b}\sqrt{\dfrac{b}{a}}=\sqrt{\dfrac{a}{b}}+\sqrt{\dfrac{a}{b}}=2\sqrt{\dfrac{a}{b}}=\dfrac{2\sqrt{ab}}{b}\)
⇒ Chọn B
Câu 18:
\(\dfrac{-8}{2\sqrt{2}}=-2\sqrt{2}\)
⇒ Chọn C
Đúng 3
Bình luận (0)
Câu 14. A
Câu 15. C
Câu 16. A
Câu 17. B
Câu 18. C
Đúng 0
Bình luận (0)
11
Với `b>0` thì:
\(2b^2\sqrt{\dfrac{a^4}{4b^2}}\\ =\sqrt{\dfrac{a^4.2b^2.2b^2}{4b^2}}\\ =\sqrt{\dfrac{a^4b^2}{1}}\\ =\sqrt{a^4b^2}\\ =a^2b\)
chọn B
12
Với `a>0`, `b>0` thì:
\(2b\sqrt{\dfrac{a}{b^2}}\\ =\sqrt{\dfrac{a.2b.2b}{b^2}}\\ =\sqrt{\dfrac{4ab^2}{b^2}}\\ =\sqrt{4a}=2\sqrt{a}\)
chọn B
13
Với `a<0`, `b<0` thì:
\(a\sqrt{\dfrac{b}{a}}\\ =\sqrt{\dfrac{b.a^2}{a}}\\ =\sqrt{b.a}\)
chọn A
Đúng 2
Bình luận (0)
Câu 6:
\(\sqrt{x}=a\)
Để phương trình có nghiệm khi: \(a>0\)
⇒ Chọn B
Câu 7:
\(\sqrt{x}=-a\)
Để phương trình có nghiệm thì: \(a< 0\)
⇒ Chọn A
Câu 8:
\(\sqrt{\dfrac{-2x}{3}}\) không có nghĩa khi:
\(\dfrac{-2x}{3}\le0\Leftrightarrow-2x\le0\Leftrightarrow x\ge0\)
⇒ Chọn C
Câu 9:
\(\sqrt{15-6\sqrt{6}}+\sqrt{15+6\sqrt{6}}=\sqrt{\left(3-\sqrt{6}\right)^2}+\sqrt{\left(3+\sqrt{6}\right)^2}=6\)
⇒ Chọn C
Đúng 0
Bình luận (0)
Câu 17.
\(\dfrac{x-3}{\sqrt{x}-\sqrt{3}}=\dfrac{\left(\sqrt{x}-\sqrt{3}\right)\left(\sqrt{x}+\sqrt{3}\right)}{\sqrt{x}-\sqrt{3}}=\sqrt{x}+3\)
⇒ Chọn D
Câu 18.
\(x^2-7=x^2-\left(\sqrt{7}\right)^2=\left(x-\sqrt{7}\right)\left(x+\sqrt{7}\right)\)
⇒ Chọn A
Câu 19.
Ta có:
\(A=-x+2\sqrt{x}+5\)
\(A=-\left(x-2\sqrt{x}-5\right)\)
\(A=-\left(x-2\sqrt{x}+1-6\right)\)
\(A=-\left[\left(\sqrt{x}-1\right)^2-6\right]\)
\(A=-\left(\sqrt{x}-1\right)^2+6\)
Mà: \(-\left(\sqrt{x}-1\right)^2\le0\forall x\) nên \(A=-\left(\sqrt{x}-1\right)^2+6\le6\)
Dấu "=" xảy ra:
\(-\left(\sqrt{x}-1\right)^2+6=6\)
\(\Leftrightarrow x=1\)
Vậy: \(A_{min}=6\) khi \(x=1\)
⇒ Chọn B
Câu 20.
Ta có:
\(B=x-4\sqrt{x}+3\)
\(B=\left(x-4\sqrt{x}+4\right)-1\)
\(B=\left(\sqrt{x}-2\right)^2-1\)
Mà: \(\left(\sqrt{x}-2\right)^2\ge0\forall x\) nên \(B=\left(\sqrt{x}-2\right)^2-1\ge-1\)
Dấu "=" xảy ra:
\(\left(\sqrt{x}-2\right)^2-1=-1\)
\(\Leftrightarrow x=4\)
Vậy: \(B_{min}=-1\) khi \(x=4\)
⇒ Chọn B
Đúng 1
Bình luận (0)
Câu 14:
\(\sqrt{x^2-6x+9}=3\)
\(\Leftrightarrow\sqrt{\left(x-3\right)^2}=3\)
\(\Leftrightarrow\left|x-3\right|=3\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=3\left(x\ge3\right)\\x-3=-3\left(x< 3\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=6\left(tm\right)\\x=0\left(tm\right)\end{matrix}\right.\)
⇒ Chọn D
Câu 15.
\(x-3=\left(\sqrt{x}\right)^2-\left(\sqrt{3}\right)^2=\left(\sqrt{x}-\sqrt{3}\right)\left(\sqrt{x}+\sqrt{3}\right)\)
⇒ Chọn B
Câu 16:
\(x-5\sqrt{x}+6=\sqrt{x}-2\sqrt{x}-3\sqrt{x}+6\)
\(=\sqrt{x}\left(\sqrt{x}-2\right)-3\left(\sqrt{x}-2\right)=\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)\)
⇒ Chọn D
Đúng 2
Bình luận (0)
Câu 7:
\(\sqrt{\left(-2x+1\right)^2}=\left|-2x+1\right|\)
⇒ Chọn B
Câu 8:
\(\sqrt{x^2}=-5\)
\(\Rightarrow\left|x\right|=-5\) (vô lý)
⇒ Chọn D
Câu 9:
\(\sqrt{16x^3y^5}=\sqrt{\left(4xy^2\right)^2xy}=4\left|x\right|y^2\sqrt{xy}\)
⇒ Chọn C
Câu 10:
\(\sqrt{8}+\sqrt{18}-\sqrt{50}=2\sqrt{2}+3\sqrt{2}-5\sqrt{2}=0\)
⇒ Chọn C
Câu 11:
\(\sqrt{6+2\sqrt{5}}+\sqrt{6-2\sqrt{5}}=\sqrt{\left(\sqrt{5}+1\right)^2}+\sqrt{\left(\sqrt{5}-1\right)^2}=\sqrt{5}+1+\sqrt{5}-1=2\sqrt{5}\)
⇒ Chọn D
Đúng 1
Bình luận (0)
1) \(\sqrt{25}=5\)
⇒ Chọn B
2) \(\sqrt{36}=6\)
⇒ Chọn A
3) Ta có: \(2\sqrt{11}=\sqrt{44}\)
Và: \(34=\sqrt{1196}\)
\(\Rightarrow2\sqrt{11}< 34\)
⇒ Chọn A
4) \(3+2x\ge0\Leftrightarrow2x\ge-3\Leftrightarrow x\ge-\dfrac{3}{2}\)
⇒ Chọn C
5) \(2x^2+5\ge0\forall x\)
\(\Rightarrow\forall x\in R\)
⇒ Chọn D
6) \(\sqrt{\left(-x-\sqrt{3}\right)^2}=\left|\left(-x-\sqrt{3}\right)\right|\)
⇒ Chọn C
7) \(\sqrt{\left(-2x+1\right)^2}=\left|-2x+1\right|\)
⇒ Chọn B
Đúng 1
Bình luận (0)
15.
a) \(\sqrt{x}=12\)
\(\Leftrightarrow x=12^2=144\)
⇒ Chọn B
b). \(5\sqrt{x}=70\)
\(\Leftrightarrow\sqrt{x}=14\)
\(\Leftrightarrow x=14^2=196\)
⇒ Chọn C
c) \(\sqrt{x}< \sqrt{3}\)
\(\Leftrightarrow x< 3\)
Mà: \(x\ge0\)
\(\Leftrightarrow0\le x< 3\)
⇒ Chọn B
d) \(\sqrt{3x}< 6\)
\(\Leftrightarrow\sqrt{3x}< \sqrt{36}\)
\(\Leftrightarrow3x< 36\)
\(\Leftrightarrow x< 12\)
Mà: \(x\ge0\) nên
\(\Rightarrow0\le x< 12\)
⇒ Chọn C
Đúng 2
Bình luận (0)
15:
a: B
b: C
c: B
d: C
14:
a: <
b: <
c: >
d: >
Đúng 1
Bình luận (0)