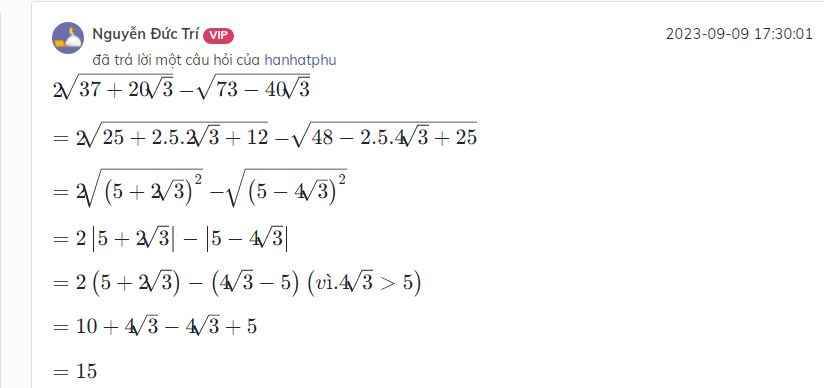Bài 1: Căn bậc hai

a: ĐKXĐ: \(2x-4>=0\)

=>x>=2

b: ĐKXĐ: \(\dfrac{1}{2-x}>=0\)

=>\(2-x>0\)

=>x<2

c: ĐKXĐ: \(-\dfrac{3}{2-6x}>=0\)

=>\(\dfrac{3}{6x-2}>=0\)

=>\(6x-2>0\)

=>x>1/3

d: ĐKXĐ: \(3x^2+2014>=0\)

=>\(x\in R\)

help

f: ĐKXĐ: \(\dfrac{2x-1}{2-x}>=0\)

=>\(\dfrac{2x-1}{x-2}< =0\)

=>\(\dfrac{1}{2}< =x< 2\)

g: ĐKXĐ: \(\left\{{}\begin{matrix}x-3>=0\\5-x>0\end{matrix}\right.\Leftrightarrow3< =x< 5\)

h: ĐKXĐ: \(\left\{{}\begin{matrix}x-1>=0\\x+5>=0\end{matrix}\right.\Leftrightarrow x>=1\)

Ta có hai hằng đẳng thức:

\(\left(a-b\right)=a^2-2ab+b^2\)

\(\left(b-a\right)^2=b^2-2ab+a^2\) 

Nhìn vào bước (1) ở VT: \(a^2-ab+b^2\)  

Mà: \(a^2-ab+b^2\ne a^2-2ab+b^2\)

Vậy sai ngay ở bước (1) 

Bang1

\(P=\dfrac{2-\sqrt{x}}{\sqrt{x}+1}=\dfrac{3-\sqrt{x}-1}{\sqrt{x}+1}=\dfrac{3}{\sqrt{x}+1}-1\)

Vì \(\sqrt{x}\ge0\Rightarrow\dfrac{3}{\sqrt{x}+1}\le3\Rightarrow P\le2\)

Vậy min của P = 2 khi x = 0

Bạn đăng bài cần giúp lên nhé!

  giúp mình nha!Thanks😘🥰😍

ĐKXĐ: x>=0 và 1-y>=0

=>x>=0 và y<=1

\(\sqrt{x\left(1-y\right)}=\sqrt{x}\cdot\sqrt{1-y}\) nó sẽ đúng khi cả hai biểu thức \(\sqrt{x};\sqrt{1-y}\) đều cùng xác định trên R

Do đó: Đẳng thức này sẽ đúng với \(\left\{{}\begin{matrix}x>=0\\y< =1\end{matrix}\right.\)

Căn bậc hai số học của 17 là \(\sqrt{17}\)

Căn bậc hai của 17 là \(\pm\sqrt{17}\)

Căn bậc hai số học của 19 là \(\sqrt{19}\)

Căn bậc hai của 19 là \(\pm\sqrt{19}\)

Chiều cao của tòa nhà là:

\(55\cdot tan55\simeq78,55\left(m\right)\)