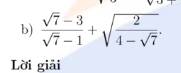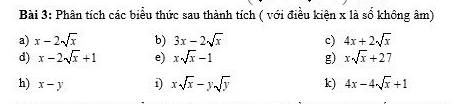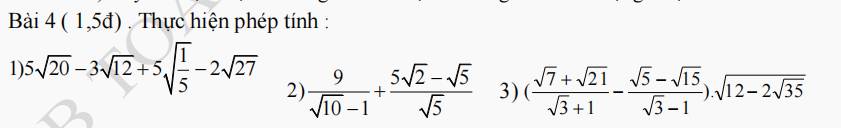(X/X-4 -√x/√x-2) / √x/√x-2
Bài 1: Căn bậc hai
\(\left(\dfrac{x}{x-4}-\dfrac{\sqrt{x}}{\sqrt{x}-2}\right):\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
\(=\left(\dfrac{x-\sqrt{x}\left(\sqrt{x}+2\right)}{x-4}\right):\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
\(=\left(\dfrac{x-x-2\sqrt{x}}{x-4}\right):\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
\(=\dfrac{-2\sqrt{x}}{x-4}:\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
\(=\dfrac{-2\sqrt{x}\left(\sqrt{x}-2\right)}{\sqrt{x}\left(x-4\right)}\)
\(=-\dfrac{2}{\sqrt{x}+2}\)
Đúng 2
Bình luận (0)
\(=\dfrac{x-\sqrt{x}\left(\sqrt{x}+2\right)}{x-4}\cdot\dfrac{\sqrt{x}-2}{\sqrt{x}}\)
\(=\dfrac{x-x-2\sqrt{x}}{\sqrt{x}+2}\cdot\dfrac{1}{\sqrt{x}}=\dfrac{-2\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)}=-\dfrac{2}{\sqrt{x}+2}\)
Đúng 1
Bình luận (0)
2.b)4√8-√18-6√1/2-√200
3.a)(a√6/a+√2a/3+√6a):√6a (a>0)
b)2/3a-1*√3a^2(9a^2-6a+1) (1/3>a>0)
2b: \(=8\sqrt{2}-3\sqrt{2}-3\sqrt{2}-10\sqrt{2}=-8\sqrt{2}\)
3:
a: \(=\left(\sqrt{6a}+\dfrac{\sqrt{6a}}{3}+\sqrt{6a}\right):\sqrt{6a}\)
=1+1/3+1
=7/3
b: \(=\dfrac{2}{3a-1}\cdot\sqrt{3}\cdot a\cdot\left|3a-1\right|\)
\(=\dfrac{2\sqrt{3}\cdot a\left(1-3a\right)}{3a-1}=-2a\sqrt{3}\)
Đúng 1
Bình luận (0)
8:
a: ĐKXĐ: \(x\in R\)
\(\sqrt{\left(x-3\right)^2}=3-x\)
=>|x-3|=3-x
=>x-3<=0
=>x<=3
b: ĐKXĐ: \(x\in R\)
\(\sqrt{4x^2-20x+25}+2x=5\)
=>\(\left|2x-5\right|=5-2x\)
=>2x-5<=0
=>x<=5/2
c: ĐKXĐ: \(x\in R\)
\(\sqrt{36x^2-12x+1}=5\)
=>|6x-1|=5
=>6x-1=5 hoặc 6x-1=-5
=>6x=6 hoặc 6x=-4
=>x=-2/3 hoặc x=1
9:
a: ĐKXĐ: \(\left\{{}\begin{matrix}2x+5>=0\\1-x>=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=-\dfrac{5}{2}\\x< =1\end{matrix}\right.\)
\(\sqrt{2x+5}=\sqrt{1-x}\)
=>2x+5=1-x
=>3x=-4
=>x=-4/3(nhận)
b: ĐKXĐ: \(\left\{{}\begin{matrix}x^2-x>=0\\3-x>=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< =3\\\left[{}\begin{matrix}x>=1\\x< =0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}1< =x< =3\\x< =0\end{matrix}\right.\)
\(\sqrt{x^2-x}=\sqrt{3-x}\)
=>x2-x=3-x
=>x2=3
=>\(x=\sqrt{3}\left(nhận\right);x=-\sqrt{3}\left(nhận\right)\)
c: ĐKXĐ: \(\left\{{}\begin{matrix}2x^2-3>=0\\4x-3>=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2>=\dfrac{3}{2}\\x>=\dfrac{3}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x>=\sqrt{\dfrac{3}{2}}\\x< =-\dfrac{\sqrt{3}}{2}\end{matrix}\right.\\x>=\dfrac{3}{4}\end{matrix}\right.\Leftrightarrow x>=\dfrac{3}{4}\)
\(\sqrt{2x^2-3}=\sqrt{4x-3}\)
=>2x^2-3=4x-3
=>2x^2-4x=0
=>2x(x-2)=0
=>x=2(nhận) hoặc x=0(loại)
Đúng 1
Bình luận (0)
ai đó biết rút gọn cứu tôi với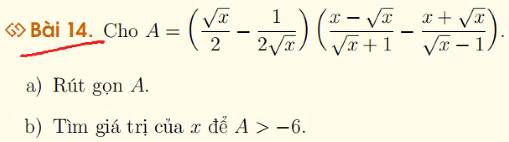
a: \(A=\left(\dfrac{x-1}{2\sqrt{x}}\right)\cdot\dfrac{\left(x-\sqrt{x}\right)\left(\sqrt{x}-1\right)-\left(x+\sqrt{x}\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}\left(x-2\sqrt{x}+1-x-2\sqrt{x}-1\right)}{2\sqrt{x}}=\dfrac{-4\sqrt{x}}{2}=-2\sqrt{x}\)
b: A>-6
=>2căn x<6
=> căn x<3
=>0<x<9 và x<>1
Đúng 0
Bình luận (0)
\(\sqrt{\left(\sqrt{3}-2\right)^2}+\sqrt{\left(1+\sqrt{3}\right)^2}\)
Có phải bằng 3 không? giúp mình
\(\sqrt{\left(\sqrt{3}-2\right)^2}+\sqrt{\left(1+\sqrt{3}\right)^2}\)
\(=\left|\sqrt{3}-2\right|+\left|1+\sqrt{3}\right|\)
\(=2-\sqrt{3}+1+\sqrt{3}\)
\(=3\)
Đúng 2
Bình luận (2)
a) \(x-2\sqrt{x}\)
\(=\sqrt{x}\left(\sqrt{x}-2\right)\)
b) \(3x-2\sqrt{x}\)
\(=\sqrt{x}\left(3\sqrt{x}-2\right)\)
c) \(4x+2\sqrt{x}\)
\(=2\sqrt{x}\left(2\sqrt{x}+1\right)\)
d) \(x-2\sqrt{x}+1\)
\(=\left(\sqrt{x}-1\right)^2\)
e) \(x\sqrt{x}-1\)
\(=\left(\sqrt{x}\right)^3-1\)
\(=\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)\)
g) \(x\sqrt{x}+27\)
\(=\left(\sqrt{x}\right)^3+3^3\)
\(=\left(\sqrt{x}+3\right)\left(x+3\sqrt{x}+9\right)\)
h) \(x-y\)
\(=\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)\)
i) \(x\sqrt{x}-y\sqrt{y}\)
\(=\left(\sqrt{x}\right)^3-\left(\sqrt{y}\right)^3\)
\(=\left(\sqrt{x}-\sqrt{y}\right)\left(x+\sqrt{xy}+y\right)\)
k) \(4x-4\sqrt{x}+1\)
\(=\left(2\sqrt{x}-1\right)^2\)
Đúng 1
Bình luận (1)
Phân tích đa thức thành nhân tử
căn ab - căn a - căn b + 1
\(=\sqrt{a}\left(\sqrt{b}-1\right)-\left(\sqrt{b}-1\right)\)
\(=\left(\sqrt{b}-1\right)\left(\sqrt{a}-1\right)\)
Đúng 0
Bình luận (0)
\(\sqrt{ab}-\sqrt{a}-\sqrt{b}+1\)
\(=\left(\sqrt{ab}-\sqrt{a}\right)-\left(\sqrt{b}-1\right)\)
\(=\sqrt{a}\left(\sqrt{b}-1\right)-\left(\sqrt{b}-1\right)\)
\(=\left(\sqrt{b}-1\right)\left(\sqrt{a}-1\right)\)
Đúng 0
Bình luận (2)
1) \(5\sqrt{20}-3\sqrt{12}+5\sqrt{\dfrac{1}{5}}-2\sqrt{27}\)
\(=5\cdot2\sqrt{5}-3\cdot2\sqrt{3}+\sqrt{25\cdot\dfrac{1}{5}}-2\cdot3\sqrt{3}\)
\(=10\sqrt{5}-6\sqrt{3}+\sqrt{5}-6\sqrt{3}\)
\(=11\sqrt{5}\)
2) \(\dfrac{9}{\sqrt{10}-1}+\dfrac{5\sqrt{2}-\sqrt{5}}{\sqrt{5}}\)
\(=\dfrac{9\left(\sqrt{10}+1\right)}{\left(\sqrt{10}-1\right)\left(\sqrt{10}+1\right)}+\dfrac{\sqrt{5}\left(\sqrt{10}-1\right)}{\sqrt{5}}\)
\(=\dfrac{9\left(\sqrt{10}+1\right)}{10-1}+\sqrt{10}-1\)
\(=\sqrt{10}+1+\sqrt{10}-1\)
\(=2\sqrt{10}\)
3) \(\left(\dfrac{\sqrt{7}-\sqrt{21}}{\sqrt{3}+1}-\dfrac{\sqrt{5}-\sqrt{15}}{\sqrt{3}-1}\right)\cdot\sqrt{12-2\sqrt{35}}\)
\(=\left(\dfrac{\sqrt{7}\left(1+\sqrt{3}\right)}{\sqrt{3}+1}-\dfrac{\sqrt{5}\left(1-\sqrt{3}\right)}{\sqrt{3}-1}\right)\sqrt{12-2\sqrt{35}}\)
\(=\left(\sqrt{7}+\sqrt{5}\right)\sqrt{\left(\sqrt{7}\right)^2-2\cdot\sqrt{7}\cdot\sqrt{5}+\left(\sqrt{5}\right)^2}\)
\(=\left(\sqrt{7}+\sqrt{5}\right)\sqrt{\left(\sqrt{7}-\sqrt{5}\right)^2}\)
\(=\left(\sqrt{7}+\sqrt{5}\right)\left|\sqrt{7}-\sqrt{5}\right|\)
\(=\left(\sqrt{7}+\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)\)
\(=\left(\sqrt{7}\right)^2-\left(\sqrt{5}\right)^2\)
\(=7-5\)
\(=2\)
Đúng 2
Bình luận (0)
1: \(=5\cdot2\sqrt{5}-3\cdot2\sqrt{3}-2\cdot3\sqrt{3}+\sqrt{5}\)
=11căn 5-12căn 3
2: \(=\sqrt{10}+1+\sqrt{10}-1=2\sqrt{10}\)
3: \(=\left(\dfrac{\sqrt{7}\left(\sqrt{3}+1\right)}{\sqrt{3}+1}+\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}\right)\cdot\left(\sqrt{7}-\sqrt{5}\right)\)
=(căn 7+căn 5)(căn 7-căn 5)
=7-5
=2
Đúng 0
Bình luận (0)