a: \(x^3-3x+2\)
\(=x^3-x-2x+2\)
\(=\left(x^3-x\right)-\left(2x-2\right)\)
\(=x\left(x^2-1\right)-2\left(x-1\right)\)
\(=x\left(x-1\right)\left(x+1\right)-2\left(x-1\right)\)
\(=\left(x-1\right)\left(x^2+x-2\right)\)
\(=\left(x-1\right)\left(x^2+2x-x-2\right)\)
\(=\left(x-1\right)\left(x+2\right)\left(x-1\right)\)
\(=\left(x+2\right)\cdot\left(x-1\right)^2\)
b: \(9x^3+3x^2-8x-4\)
\(=9x^3-9x^2+12x^2-12x+4x-4\)
\(=9x^2\left(x-1\right)+12x\left(x-4\right)+4\left(x-1\right)\)
\(=\left(x-1\right)\left(9x^2+12x+4\right)\)
\(=\left(x-1\right)\left(3x+2\right)^2\)
c: \(6x^4-11x^2+3\)
\(=6x^4-9x^2-2x^2+3\)
\(=3x^2\left(2x^2-3\right)-\left(2x^2-3\right)\)
\(=\left(2x^2-3\right)\left(3x^2-1\right)\)
\(a,x^3-3x+2\\=x^3-x-2x+2\\=x(x^2-1)-2(x-1)\\=x(x-1)(x+1)-2(x-1)\\=(x-1)[x(x+1)-2]\\=(x-1)(x^2+x-2)\\=(x-1)(x^2-x+2x-2)\\=(x-1)[x(x-1)+2(x-1)]\\=(x-1)^2(x+2)\)
\(b,9x^3+3x^2-8x-4\\=9x^3-9x^2+12x^2-12x+4x-4\\=9x^2(x-1)+12x(x-1)+4(x-1)\\=(x-1)(9x^2+12x+4)\\=(x-1)[(3x)^2+2\cdot 3x\cdot2+2^2]\\=(x-1)(3x+2)^2\)
\(c,6x^4-11x^2+3\\=6x^4-2x^2-9x^2+3\\=2x^2(3x^2-1)-3(3x^2-1)\\=(3x^2-1)(2x^2-3)\\\text{#}Toru\)
`#3107.101107`
`7.`
`a)`
`x^3 - 3x + 2`
`= x^3 - 2x - x + 2`
`= (x^3 - x) - (2x - 2)`
`= x(x^2 - 1) - 2(x - 1)`
`= x(x - 1)(x + 1) - 2(x - 1)`
`= [ x(x + 1) - 2](x - 1)`
`= (x^2 + x - 2)(x - 1)`
`= (x - 1)(x + 2)(x - 1)`
`= (x - 1)^2 (x + 2)`
`b)`
`9x^3 + 3x^2 - 8x - 4`
`= 9x^3 + 12x^2 - 9x^2 + 4x - 12x - 4`
`= (9x^3 + 12x^2 + 4x) - (9x^2 + 12x + 4)`
`= x(9x^2 + 12x + 4) - (9x^2 + 12x + 4)`
`= (x - 1)(9x^2 + 12x + 4)`
`= (x - 1)(3x + 2)^2`
`c)`
`6x^4 - 11x^2 + 3`
`= 6x^4 - 2x^2 - 9x^2 + 3`
`= (6x^4 - 2x^2) - (9x^2 - 3)`
`= 2x^2(3x^2 - 1) - 3(3x^2 - 1)`
`= (2x^2 - 3)(3x^2 - 1)`
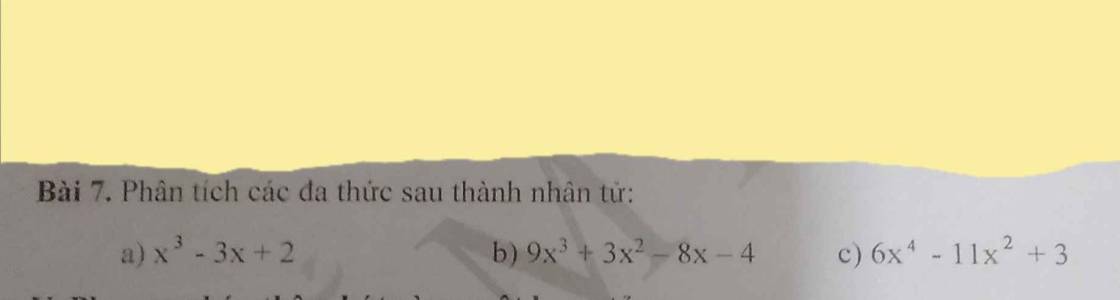
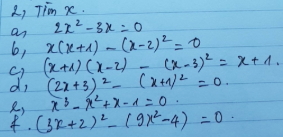Không làm tắt