a) 2x2-3x=0
\(\Rightarrow\)x(2x-3)=0
\(\Rightarrow\)\(\left[{}\begin{matrix}x=0\\2x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\2x=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{3}{2}\end{matrix}\right.\)
c) (x+1)(x-2)-(x-3)2=x+1
⇒(x+1)(x-2)-(x-3)2-(x+1)=0
\(\Rightarrow\)x2-2x+x-2-(x2-6x+9)-x-1=0
⇒x2-2x+x-2-x2+6x-9-x-1=0
\(\Rightarrow\)4x-12=0
\(\Rightarrow\)4x=12
\(\Rightarrow\)x=3
d)(2x+3-x-1)(2x+3+x+1)=(x+2)(3x+4)=3x2+4x+6x+8=3x2+10x+8
e)x3-x2+x-1=0
\(\Rightarrow\)(x3-x2)+(x-1)=0
\(\Rightarrow\)x2(x-1)+(x-1)=0
\(\Rightarrow\)(x-1)(x2+1)=0
\(\Rightarrow\)x-1=0 hoặc x2+1=0
\(\Rightarrow\left[{}\begin{matrix}x-1=0\\x^2+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x^2=-1\left(KTĐTSx\right)\end{matrix}\right.\)
KTĐTSx: không tìm được thừa số x
Vậy S={1}
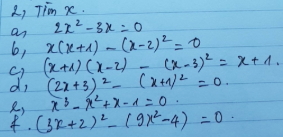 Không làm tắt
Không làm tắt
