Cho đa thức \(f\left(x\right)=x^2+4x-5\). Viết tập hợp S tất cả các nghiệm của f (x)
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
KT
Những câu hỏi liên quan
Bài 1: Cho đa thức f(x) = x2 + 4x - 5
a) Số -5 có phải là nghiệm của f(x) không?
b) Viết tập hợp S tất cả các nghiệm của f(x)
a: \(f\left(-5\right)=\left(-5\right)^2+4\cdot\left(-5\right)-5=0\)
=>x=-5 là nghiệm của f(x)
b: S={-5;1}
Đúng 4
Bình luận (0)
Cho đa thức f(x) = x2 +4x -5
a) Số -5 có phải nghiệm của đa thức f(x) ko?
b) Viết tập hợp S tất cả các nghiệm của f(x)
a, Ta có: Với x = -5
→ f(-5) = (-5)2 + 4.(-5) - 5
= 25 + ( -20 ) - 5
= 5 - 5 = 0
Vì f(-5) = 0 nên x = -5 là nghiệm của đa thức f(x)
Đúng 0
Bình luận (0)
Cho đa thức f(x) = x^2=4x-5
a/ Số -5 có phải là nghiệm của f(x) không ?
b/ Viết tập hợp S tất cả các nghiệm của f(x)
a. Số -5 không phải là nghiệm của f(x).
b. \(S=\varnothing\)
Đúng 0
Bình luận (0)
Cho 2 đa thức:
f(x) = x2 - 6x + 5 và h(x) = x4 + 1/5.x2 + 2012
a. Trong tập hợp số { 5; 3; -1;0} số nào là nghiệm số nào không là nghiệm của đa thức
b. Hãy viết tập hợp S tất cả các nghiệm của f(x)
c. Hãy c/m đa thức h(x) không có nghiệm
Giúp mik với
a) ta có:
+) x = 5 => f(5) = 52 - 6.5 + 5 = 25 - 30 + 5 = 0
=> x = 5 là nghiệm của f(x)
+) x = 3 => f(3) = 32 - 6.3 + 5 = 9 - 18 + 5 = -4
=> x = 3 ko là nghiệm của f(x)
+) x = 1 =. f(1) = 12 - 6.1 + 5 = 1 - 6 + 5 = 0
=> x = 1 là nghiệm của f(x)
+) x = 0 => f(0) = 02 - 6.0 + 5 = 5
=> x = 5 ko là nghiệm của f(x)
b) Tập hợp S = {5; -1}
c) Ta có : x4 \(\ge\)0 ; 1/5x2 \(\ge\)0 ; 2012 > 0
=> x4 + 1/5x2 + 2012 > 0
=> đa thức h(x) ko có nghiệm
Đúng 0
Bình luận (0)
\(a.\)Thay lần lượt các giá trị của \(x\)trong tập hợp số \(\left\{5;3;-1;0\right\}\)vào đa thức \(f\left(x\right)\)như bn Edogawa Conan nha !
Ta thấy \(f\left(5\right)=5^2-6.5+5=0\)nên \(x=5\)là 1 ngiệm của \(f\left(x\right)\)
\(b.\)Ta có: \(f\left(x\right)=x^2-x-5x+5=x\left(x-1\right)-5\left(x-1\right)=\left(x-1\right)\left(x-5\right)\)
\(f\left(x\right)=0\Leftrightarrow\cdot x-1\left(x-5\right)=0\Leftrightarrow\orbr{\begin{cases}x=1\\x=5\end{cases}}\)
\(c.\)Xét đa thức \(h\left(x\right)=x^4+\frac{1}{5}x^2+2012\)
Do \(x^4\ge0\)và \(\frac{1}{5}x^2\ge0\)với mọi \(x\)nên \(h\left(x\right)>0\)với mọi \(x\)
Vậy \(h\left(x\right)\ne0\)với mọi \(x\)Do đó đa thức \(h\left(x\right)\)không có nghiệm
Đúng 0
Bình luận (0)
Bài 3 : tìm nghiệm của các đa thức sau
a) 3x - 6
b) -5y + 30
c) ( z - 3 ) . ( 16 - 4z )
d) \(x^2\) - 3
Bài 4 : cho đa thức f(x) = \(x^2+4x-5\)
a) số -5 có phải nghiệm của f(x) không
b) viết tập hợp S tất cả các nghiệm của f(x)
a, \(3x-6=0\)
\(\Leftrightarrow3\left(x-2\right)=0\)
\(\Rightarrow x-2=0\Rightarrow x=2\)
b, \(-5y+30=0\)
\(\Leftrightarrow-5\left(y-6\right)=0\)
\(\Rightarrow y-6=0\Rightarrow y=6\)
c, \(\left(z-3\right)\left(16-4z\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}z-3=0\Rightarrow z=3\\16-4z=0\Leftrightarrow4\left(4-z\right)=0\Rightarrow z=4\end{matrix}\right.\)
d, \(x^2-3=0\)
\(\Rightarrow x^2=3\Rightarrow x=\sqrt{3}\)
Đúng 0
Bình luận (0)
a, -5 có phải là nghiệm của đa thức f(x)
b, \(S\in\left\{-5;1\right\}\)
Đúng 0
Bình luận (1)
Bài 3:
a) 3x - 6
+Thay x=2 vào ta được:
3.2 - 6
= 6 - 6=0
Vậy x=2 là nghiệm của đa thức 3x - 6.
b) -5y + 30
+Thay y=6 vào ta được:
(-5).6 + 30
= (-30) + 30=0
Vậy y=6 là nghiệm của đa thức -5y + 30.
c) (z - 3).(16 - 4z)
+Thay z=3 vào ta được:
(3 - 3).(16 - 4.3)
= 0.4=0
+Thay z=4 vào ta được:
(4 - 3).(16 - 4.4)
= 1.0=0
Vậy z=3 và z=4 đều là nghiệm của đa thức (z - 3).(16 - 4z).
d) x2 - 3
+Thay x=√3 vào ta được:
√32 - 3
= 3 - 3=0
Vậy x=√3 là nghiệm của đa thức x2 - 3.
Bài 4:
a) Số -5 có phải là nghiệm của đa thức f(x).
b) S = {-5; 1}
Chúc bạn học tốt!
Đúng 0
Bình luận (0)
Cho hàm số đa thức bậc ba yf(x) có đồ thị của các hàm số yf(x), yf (x)như hình vẽ bên.Gọi S là tập hợp tất cả các giá trị nguyên của m để phương trình f(f(x)-m)+2f(x)3(x+m) có đúng 3 nghiệm thực .Tổng các phần tử của S bằng A. 0 B. -6 C. -7 D. -5
Đọc tiếp
Cho hàm số đa thức bậc ba y=f(x) có đồ thị của các hàm số y=f(x), y=f '(x)như hình vẽ bên.Gọi S là tập hợp tất cả các giá trị nguyên của m để phương trình f(f(x)-m)+2f(x)=3(x+m) có đúng 3 nghiệm thực .Tổng các phần tử của S bằng
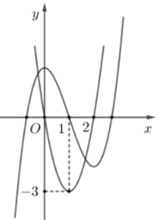
A. 0
B. -6
C. -7
D. -5
Ta có ![]()
![]()
Quan sát đồ thị có 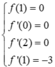
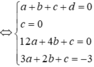

![]()
Đặt ![]() phương trình trở thành:
phương trình trở thành:
![]()
![]()
![]()
Khi đó ![]()
Phương trình này có 3 nghiệm phân biệt
![]()
Tổng các phần tử củaS bằng 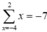
Chọn đáp án C.
Đúng 0
Bình luận (0)
Cho các hàm số \(f\left(x\right)=x^2-4x+m\) và \(g\left(x\right)=\left(x^2+1\right)\left(x^2+2\right)^2\left(x^2+3\right)^3\) . Tìm tập hợp tất cả các giá trị của tham số m để hàm số \(g\left(f\left(x\right)\right)\) đồng biến trên \(\left(3;+\infty\right)\) .
\(g'\left(x\right)=0\Rightarrow x=0\)
Ta thấy \(g\left(x\right)\) đồng biến trên \(\left(0;+\infty\right)\)
\(\Rightarrow g\left(f\left(x\right)\right)\) đồng biến khi \(f\left(x\right)\ge0\)
\(\Rightarrow g\left(f\left(x\right)\right)\) đồng biến trên \(\left(3;+\infty\right)\) khi \(f\left(x\right)\ge0\) ; \(\forall x>3\)
\(\Leftrightarrow x^2-4x\ge-m\) ; \(\forall x>3\)
\(\Leftrightarrow-m\le\min\limits_{x>3}\left(x^2-4x\right)\)
\(\Rightarrow-m\le-3\Rightarrow m\ge3\)
Đúng 2
Bình luận (0)
Cho hàm số f(x) = \(\dfrac{x+m}{x+1}\) (m là tham số thực). Gọi S là tập hợp tất cả các giá trị của tham số m sao cho \(max_{[0;1]}\left|f\left(x\right)\right|\) + \(min_{[0;1]}\left|f\left(x\right)\right|\) =2. Số phần tử của S là?
Xét hàm \(f\left(x\right)=\dfrac{x+m}{x+1}\) có \(f'\left(x\right)=\dfrac{\left(x+m\right)'\left(x+1\right)-\left(x+m\right)\left(x+1\right)'}{\left(x+1\right)^2}=\dfrac{1-m}{\left(x-1\right)^2}\)
Cho \(f'\left(x\right)=\dfrac{1-m}{\left(x-1\right)^2}=0\Leftrightarrow m=1\)
Khi đó \(f\left(x\right)=\dfrac{x+1}{x+1}=1\)
\(\Rightarrow max_{\left[0;1\right]}\left|f\left(x\right)\right|+min_{\left[0;1\right]}\left|f\left(x\right)\right|=1+1=2\) ( thỏa mãn )
Vậy \(m=1\) thỏa mãn bài toán.
Xét \(m\ne1\), ta thấy \(f\left(x\right)\) đơn điệu trên \(\left[0;1\right]\), xét các trường hợp:
*) \(f\left(0\right).f\left(1\right)\le0\Leftrightarrow\dfrac{m+1}{2}\cdot m\le0\) \(\Leftrightarrow-1\le m\le0\)
\(\Rightarrow\left\{{}\begin{matrix}min_{\left[0;1\right]}\left|f\left(x\right)\right|=0\\max_{\left[0;1\right]}\left|f\left(x\right)\right|=max\left\{\dfrac{\left|m+1\right|}{2};\left|m\right|\right\}\end{matrix}\right.\)
Khi đó: \(max_{\left[0;1\right]}\left|f\left(x\right)\right|+min_{\left[0;1\right]}\left|f\left(x\right)\right|=2\)
\(\Leftrightarrow0+\dfrac{\left|\dfrac{m+1}{2}+m\right|+\left|\dfrac{m+1}{2}-m\right|}{2}=2\)
\(\Leftrightarrow\left|\dfrac{3m+1}{2}\right|+\left|\dfrac{-m+1}{2}\right|=4\)
\(\Leftrightarrow\left|3m+1\right|+\left|m-1\right|=8\) (1)
Xét các trường hợp:
+) \(m\le\dfrac{-1}{3}\) : \(\left(1\right)\Leftrightarrow-3m-1-m+1=8\Leftrightarrow m=-2\) ( loại )
+) \(m\ge1\) : \(\left(1\right)\Leftrightarrow3m+1+m-1=8\Leftrightarrow m=2\) ( loại )
+) \(-\dfrac{1}{3}< m< 1\) : \(\left(1\right)\Leftrightarrow3m+1-m+1=8\Leftrightarrow m=3\) ( loại )
*) \(f\left(0\right)\cdot f\left(1\right)>0\Leftrightarrow\dfrac{m+1}{2}\cdot m>0\Leftrightarrow\left[{}\begin{matrix}m>0\\m< -1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}min_{\left[0;1\right]}\left|f\left(x\right)\right|=min\left\{\dfrac{\left|m+1\right|}{2};\left|m\right|\right\}\\max_{\left[0;1\right]}\left|f\left(x\right)\right|=max\left\{\dfrac{\left|m+1\right|}{2};\left|m\right|\right\}\end{matrix}\right.\)
Khi đó: \(min_{\left[0;1\right]}\left|f\left(x\right)\right|+max_{\left[0;1\right]}\left|f\left(x\right)\right|=2\)
\(\Leftrightarrow\dfrac{\left|\left|\dfrac{m+1}{2}+m\right|-\left|\dfrac{m+1}{2}-m\right|\right|}{2}+\dfrac{\left|\left|\dfrac{m+1}{2}+m\right|\right|+\left|\left|\dfrac{m+1}{2}-m\right|\right|}{2}=2\)
\(\Leftrightarrow\dfrac{\left|\left|3m+1\right|-\left|m-1\right|\right|}{4}+\dfrac{\left|\left|3m+1\right|+\left|m-1\right|\right|}{4}=2\)
\(\Leftrightarrow\dfrac{2\left|3m+1\right|}{4}=2\)
\(\Leftrightarrow\left|3m+1\right|=4\)
\(\Leftrightarrow\left[{}\begin{matrix}m=1\\m=\dfrac{-5}{3}\end{matrix}\right.\)
Tóm lại ở cả 2 trường hợp thì ta có \(m\in\left\{1;\dfrac{-5}{3}\right\}\) thỏa mãn đề bài.
Vậy \(S=\left\{1;\dfrac{-5}{3}\right\}\) có \(2\) phần tử.
Đúng 1
Bình luận (0)
Cho hàm số f(x)=\(\dfrac{x+m}{x+1}\)( m là tham số thực) gọi S là tập hợp tất cả các giá trị của m sao cho \(\min\limits_{\left[0;1\right]}\left|f\left(x\right)\right|+\max\limits_{\left[0;1\right]}\left|f\left(x\right)\right|=2\). Số phần tử của A là
A.6
B.2
C.1
D.4
Bạn tham khảo ạ!
Cho hàm số f(x) = \(\dfrac{x+m}{x+1}\) (m là tham số thực). Gọi S là tập hợp tất cả các giá trị của tham số m sao cho \(... - Hoc24
Còn nếu chưa hiểu cách làm thì bạn có thể hỏi anh Lâm hoặc chính người làm bài này :)
Đúng 1
Bình luận (0)
Lời giải:
Nếu $m=1$ thì hàm $f(x)=1$ là hàm hằng thì không có cực trị.
Nếu $m\neq 1$;
$f'(x)=\frac{1-m}{(x+1)^2}$. $m>1$ thì hàm nghịch biến trên $[0;1]$, mà $m< 1$ thì hàm số đồng biến trên $[0;1]$
Từ đó suy ra hàm số đạt cực trị tại biên, tức là $(f_{\min}, f_{\max})=(f(1),f(0))=(m, \frac{m+1}{2})$ và hoán vị.
Giờ ta đi giải PT:
$|m|+|\frac{m+1}{2}|=2$
Dễ dàng giải ra $m=1$ hoặc $m=\frac{-5}{3}$
Do đó đáp án là B.
Đúng 2
Bình luận (0)






