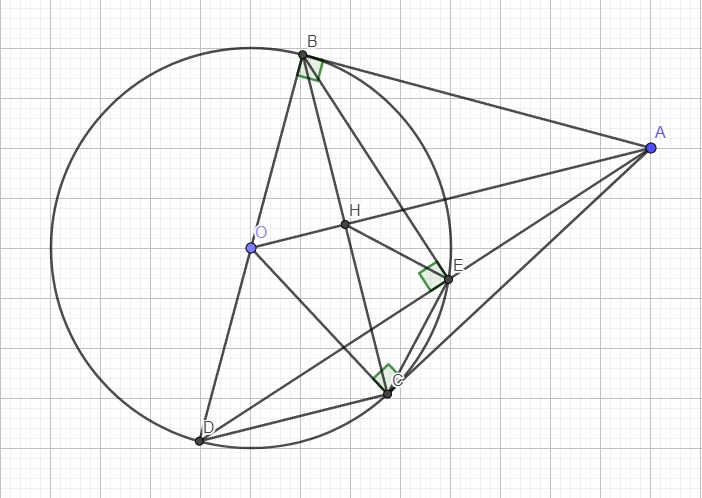
Bài 7:

a: Xét ΔAMB và ΔAMC có

AM chung

MB=MC

AB=AC

Do đó: ΔAMB=ΔAMC

b: Ta có: ΔAMB=ΔAMC

=>\(\widehat{BAM}=\widehat{CAM}\)

mà tia AM nằm giữa hai tia AB,AC

nên AM là phân giác của góc BAC

Ta có: ΔAMB=ΔAMC

=>\(\widehat{AMB}=\widehat{AMC}\)

mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)

nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)

=>AM\(\perp\)BC

c: Xét ΔDBC có

DM là đường cao

DM là đường trung tuyến

Do đó: ΔDBC cân tại D

=>DB=DC

Bài 6:

a: Xét ΔAMB và ΔEMC có

MA=ME

\(\widehat{AMB}=\widehat{EMC}\)(hai góc đối đỉnh)

MB=MC

Do đó: ΔAMB=ΔEMC

b: Ta có: ΔAMB=ΔEMC

=>\(\widehat{MAB}=\widehat{MEC}\)

mà hai góc này là hai góc ở vị trí so le trong

nên AB//EC

Ta có: AB//EC

AB\(\perp\)AC

Do đó: EC\(\perp\)AC

c: Xét ΔECA vuông tại C và ΔBAC vuông tại A có

EC=BA

AC chung

Do đó: ΔECA=ΔBAC

=>EA=BC

mà EA=2AM

nên BC=2AM

 

 

chưa vẽ được

tick cho mình cái 

 

Bài tập 1

a) Chứng minh AFOE cân

Xét tam giác AOB và tam giác FOE, ta có:

AB = FO (do B là đỉnh chéo của hình bình hành ABCD) AO = OF (do O là giao điểm của các đường chéo) AE = OF (do F nằm trên cạnh BC)

Do đó, hai tam giác AOB và FOE đồng dạng theo tỉ số 1:1.

Vậy, AFOE cân tại F.

b) Trên tia đối của tòa FB lấy điểm 1 sao cho F1 = FB. Chứng minh OF = h OE == DI

Xét tam giác F1OB và tam giác FOE, ta có:

FB = F1B (do F1 = FB) FO = OF (do O là giao điểm của các đường chéo) BE = FE (do F nằm trên cạnh BC)

Do đó, hai tam giác F1OB và FOE đồng dạng theo tỉ số 1:1.

Vậy, OF = OE = DI.

c) Gia sư BAD =50. Tính EOF

Xét tam giác EOF, ta có:

EO = OE (do O là giao điểm của các đường chéo) OF = OE = DI = 50/2 = 25

Do đó, EOF = 25^2 = 625.

Kết luận

AFOE cân tại F OF = OE = DI = 25 EOF = 625

Bài tập 2

Chứng minh 1 đổi xứng với K qua Đ

Xét tam giác AFE và tam giác BKF, ta có:

AE = CF (do cho AE = CF) AF = BF (do do A và B là các đỉnh chéo của hình bình hành ABCD) EF = FB (do F nằm trên cạnh BC)

Do đó, hai tam giác AFE và BKF đồng dạng theo tỉ số 1:1.

Vậy, I đối xứng với K qua D.

Kết luận

I đối xứng với K qua D.

Bài tập 3

Chứng minh Nạp là hai điểm đối xứng nhau qua ở

Xét tam giác MNO và tam giác MNP, ta có:

MN = MN (đồng nhất) NO = NP (do N và P lần lượt đối xứng với M qua a và b) MO = MP (do O là giao điểm của các đường chéo a và b)

Do đó, hai tam giác MNO và MNP đồng dạng theo tỉ số 1:1.

Vậy, N và P là hai điểm đối xứng nhau qua O.

Kết luận

N và P là hai điểm đối xứng nhau qua O.

Chúc bạn học tốt!

Tiểu học lớp 3

TL : 

100 mm = 10 cm

         10 cm

10 cm

~HT~

mình thiếu chữ cạnh ở chỗ độ dài của cạnh hình nha

n đường thẳng đi qua điểm M tạo thành 2n tia chung gốc M

Lấy 1 tia trong 2n tia chung gốc M tạo với 2n-1 tia , còn lại 2n-1 góc

-> Có 2n tia thì có: 2n*(2n-1) góc

Vì mỗi góc được tính 2 lần

-> Có số góc là : 2n*(2n-1):2=n*(2n-1) góc

n đường thẳng đôi một phân biệt đi qua M tạo thành n góc bẹt 

-> Có số góc nhỏ hơn góc bẹt là: n*(2n-1)-n=n*(2n-2)=n*(n-1)*2 ( góc )

Vì 2 góc là một cặp góc đối đỉnh 

-> Có số góc đối đỉnh nhỏ hơn góc bẹt là : 

                 n*(n-1)*2 : 2= n*(n-1) góc

Vậy có n*(n-1) cặp góc đối đỉnh nhỏ hơn góc bẹt.

b) Theo phần a) ta có:

               n*(n-1)=930

Ta thấy: n và n-1 là hai số liên tiếp mà 930=31*30

              =>n*(n-1)=31*30

              => n=31

Vậy n=31

Like ủng hộ mk nha!

 

a.

Do AB là tiếp tuyến của (O) \(\Rightarrow AB\perp OB\Rightarrow\Delta ABO\) vuông tại B

\(\Rightarrow\Delta ABO\) nội tiếp đường tròn đường kính OA (1)

Tương tự, do AC là tiếp tuyến của (O) \(\Rightarrow\Delta ACO\) vuông tại C

\(\Rightarrow\Delta ACO\) nội tiếp đường tròn đường kính OA (2)

(1);(2) \(\Rightarrow\)4 điểm A,B,O,C cùng thuộc đường tròn đường kính OA

b.

Do BD là đường kính và E là điểm thuộc đường tròn nên \(\widehat{BED}\) là góc nội tiếp chắn nửa đường tròn

\(\Rightarrow\widehat{BED}=90^0\)

Xét hai tam giác EAB và EBD có:

\(\left\{{}\begin{matrix}\widehat{AEB}=\widehat{BED}=90^0\\\widehat{EBA}=\widehat{EDB}\left(\text{cùng phụ }\widehat{EBD}\right)\end{matrix}\right.\) 

\(\Rightarrow\Delta EAB\sim\Delta EBD\left(g.g\right)\Rightarrow\dfrac{DE}{BE}=\dfrac{BD}{AB}\)

//\(\widehat{BCD}\) là góc nội tiếp chắn nửa đường tròn \(\Rightarrow\widehat{BCD}=90^0\)

Do \(AB=AC\) (t/c hai tiếp tuyến cắt nhau) và \(OB=OC=R\)

\(\Rightarrow OA\) là trung trực của BC \(\Rightarrow OA\perp BC\) tại H

Xét hai tam giác BCD và AHB có:

\(\left\{{}\begin{matrix}\widehat{BCD}=\widehat{AHB}=90^0\\\widehat{ABC}=\widehat{BDC}\left(\text{cùng chắn cung BC}\right)\end{matrix}\right.\)  \(\Rightarrow\Delta BCD\sim\Delta AHB\left(g.g\right)\)

\(\Rightarrow\dfrac{BD}{AB}=\dfrac{CD}{BH}\Rightarrow\dfrac{CD}{BH}=\dfrac{DE}{BE}\)

Xét hai tam giác CDE và BHE có: 

\(\left\{{}\begin{matrix}\dfrac{CD}{BH}=\dfrac{DE}{BE}\\\widehat{CDE}=\widehat{HBE}\left(\text{cùng chắn }CE\right)\end{matrix}\right.\)  \(\Rightarrow\Delta CDE\sim\Delta BHE\left(g.g\right)\)

\(\Rightarrow\widehat{CED}=\widehat{BEH}\)

Mà \(\widehat{BEH}+\widehat{DEH}=\widehat{BED}=90^0\)

\(\Rightarrow\widehat{HEC}=\widehat{CED}+\widehat{DEH}=90^0\)

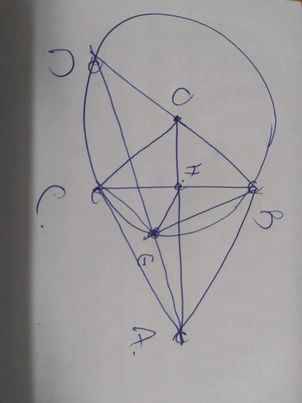
a: Ta có: ΔOBA vuông tại B

=>B,O,A cùng nằm trên đường tròn đường kính OA(1)

Ta có: ΔOCA vuông tại C

=>O,C,A cùng nằm trên đường tròn đường kính OA(2)

Từ (1) và (2) suy ra B,O,A,C cùng thuộc một đường tròn

b: Xét (O) có

ΔBED nội tiếp

BD là đường kính

Do đó: ΔBED vuông tại E

=>BE\(\perp\)ED tại E

=>BE\(\perp\)AD tại E

Xét ΔEBD vuông tại E và ΔEAB vuông tại E có

\(\widehat{EBD}=\widehat{EAB}\left(=90^0-\widehat{BDA}\right)\)

Do đó: ΔEBD~ΔEAB

=>\(\dfrac{ED}{EB}=\dfrac{BD}{AB}\)

 

Chứng minh: At // Bt'

ta có: góc xAB = góc yBz ( đồng vị) 

=> góc xAB/2 = góc yBz/2

mà góc A1 = góc xAB/2 ( tính chất tia phân giác)

góc B1 = góc yBz/2 ( tính chất tia phân giác)

=> góc A1 = góc B1 ( = góc xAB/2 = gocs yBz/2)

mà góc A1; góc B1 nằm ở vị trí đồng vị

=> At // Bt' ( định lí song song)

phải vẽ hình rồi mới xét được chứ

Câu hỏi của Xuân Phạm - Toán lớp 7 - Học toán với OnlineMath